Динаміка твердого тіла

Диференційне рівняння поступального руху твердого тіла: і т.д. X^e_i – проекція зовнішньої сили. Всі точки тіла рухаються так само, як і його центр мас С. Для виконання поступального руху необхідно, щоб головний момент всіх зовнішніх сил відносно центра мас дорівнював 0: .

Диференційне рівняння обертання твердого тіла навколо нерухомої осі: , J_z – момент інерції тіла відносно осі обертання z, М_z^e – момент зовнішніх сил відносно осі обертання (обертаючий момент). кутове прискорення, чим більше момент інерції при даному М_z^e, тим менше прискорення, тобто момент інерції при обертальному русі являється аналогом маси при поступальному. Знаючи М_z^e, можна знайти закон обертання тіла , та навпаки, знаючи, можна знайти момент. Власні випадки: 1.якщотіло обертається рівномірно; 2.обертання рівнозмінне. Рівняння аналогічне диференційному рівнянню прямолінійного руху точки

Фізичний маятник – тверде тіло, яке здійснює коливання навколо нерухомої горизонтальної осі під дією сили тяжіння. Рівняння обертального руху: , позначаючи, отримуємо

д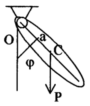иференційне рівняння коливань маятника:частота коливань маятника. Розглядаючи малі коливання, можна вважати, тодідиференційне рівняння гармонічних коливань. Розв’язок цього рівняння:абоамплітуда коливань маятника, β – початкова фаза коливань. Період малих коливань фізичного маятника. Для малих коливань маятника період не залежить від кута початкового відхилення, цей результат є нерухомим. Для математичного маятника (матеріальної точки, підвішеній на нитці, яка не розтягується, та рухається під дією сили тяжіння) має диференційне рівняння руху:довжина нитки. Якщо, то математичний маятник буде рухатися так само, як і фізичний (період коливань співпадає). Величина L називається приведеною довжиною фізичного маятника. Точка К, відстояна від осі підвісу на відстані ОК = L, називається центром качання фізичного маятника. Якщо вісь підвісу взяти в точці К, то точка О буде центром коливань і навпаки –властивість взаємності. Відстань ОК завжди > ОС, тобто центр коливань завжди розташований нижче центра мас.

Динаміка плоского руху твердого тіла

Положення тіла визначається положенням полюса та кутом повороту тіла навколо полюса. Диференційне рівняння плоского руху твердого тіла:

С – центр мас тіла, J_С – момент інерції тіла відносно осі, перпендикулярної до плоскості руху тіла та проходячій через центр його мас.

Принцип Даламбера (метод кінетостатики)

В кожний момент руху сума активних сил, реакцій зв’язків та сил інерції дорівнює нулю - принцип

Даламбера для матеріальної точки. - зовнішня сила,- внутрішня сила. Сила інерції:, знак (-) показує, що сила інерції направлена в протилежний бік прискоренню. Для системи додається рівняння моментів:. Позначають:- головний момент сил інерції. Враховуючи, що геометрична сума внутрішніх сил та сума їх моментів дорівнює нулю, отримуємо:- рівняння кінетостатики. Принцип Даламбера для системи – якщо в будь-який момент часу в кожній точці системи прокласти, окрім реально діючих сил, відповідні сили інерції, то отримана система сил буде знаходитись в рівновазі та до неї можна використати рівняння статики. Це спрощує процес розв’язання задач.

Головний вектор сил інерції дорівнює добутку маси тіла на прискорення його центра мас та направлений в протилежну сторону цьому прискоренню. Головний момент сил інерції залежить від виду руху: при поступальному русі, при плоскому, при обертанні навколо осі z, яка проходить через центр мас тіла,.

Визначення реакцій при обертанні твердого тіла навколо нерухомої осі.

П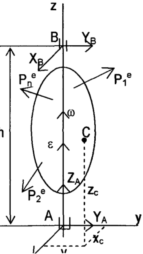ри русі тіла навколо нерухомої осі виникаютьдинамічні тиски на опори. Їх визначення добре вирішувати методом кінетостатики. Прикладаємо сили інерції для кожної точки: центробіжна , обертальна, r_i – відстань від точки до осі обертання. Проектуючи суму цих сил на осі та враховуючи, що тацентр мас, отримуємо проекції головного вектора сил інерції:

Проекції головного моменту сил інерції = сумі моментів центр обіжних та обертальних сил інерції відносно осей координат:

- центробіжні моменти інерції, .

Враховуючи зовнішні сили, можна записати рівняння рівноваги кінетостатики:

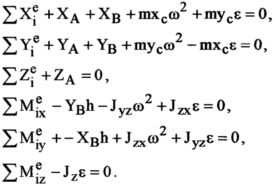
Останнє рівняння не включає реакцій опор то являє собою диференційне рівняння обертання тіла. Останні п’ять рівнянь дозволяють визначити п’ять відомих реакцій. Динамічні складові реакцій визначаються доданками, які залежать від сил інерції.

Умови відсутності динамічних складових:

, звідки , це означає, що центр тяжіння повинен знаходитись на осі обертання тіла та вісь обертання тіла z повинна бути головною віссю інерції тіла. Тобто вісь обертання повинна бути головною центробіжною віссю інерції тіла (ось, яка проходить через центр мас тіла, і центробіжні моменти інерції з індексом осі рівним нулю). Для виконання цієї умови проводиться спеціальна балансировка швидко обертаючихся тіл.