Розділ 3. Динаміка

Динаміка – розділ механіки, в якому вивчаються закони руху матеріальних тіл під дією сил. Основні закони механіки (закони Галілея – Ньютона): закон інерції (1-ий закон): матеріальна точка зберігає стан спокою рівномірного прямолінійного руху до тих пір, доки дія інших тіл не змінить цей стан; основний закон динаміки ( 2-ий закон (Ньютона)): прискорення матеріальної точки пропорційно прикладеній до неї силі та має однаковий з нею напрямок ;закон рівності дії та протидії (3-ій закон (Ньютона)): всілякій дії відповідає рівна та протилежно направлена протидія; закон незалежності сил: декілька одночасно діючих на матеріальну точку сил повідомляють точці таке прискорення, яке б повідомила їй одна сила, яка дорівнює їх геометричній сумі. В класичній механіці маса тіла, яке рухається приймається рівній масі тіла в стані спокою, - міра інертності тіла та його гравітаційних властивостей. Маса = вазі тіла, розділеній на прискорення вільного падіння, m=G/g, g= 9,81 м/с². g залежить від географічної широти місця та висоти над рівне моря – не постійна величина. Сила – 1Н (Ньютон) = 1кг ^.м/с². Система відліку, в якій проявляється 1-ий та 2-ий закони, назив. інерційною системою відліку. Диференційне рівняння матеріальної точки: , в проекції на декартові осі координат:, на осі природного трьохгранника:- проекція прискорення на бінормаль, тобто

радіус кривизни траєкторії в поточній точці). В випадку плоского руху точки в полярних координатах: . Дві основні задачі динаміки:перша задача динаміки – знаючи закон руху точки, визначити діючу на неї силу; друга задача динаміки (основна) – знаючи діючі на точку сили, визначити закон руху точки. - диференційне рівняння прямолінійного руху точки. Дворазово інтегруючи його, знаходимо загальне рішення. Постійні інтегрування С₁, С₂ шукають з початкових умов: - частинне рішення – закон руху точки.

Коливальний рух матеріальної точки. Відновлююча сила (сила пружності) сила прагне повернути точку в рівноважне положення, «с» - коефіцієнт жорсткості пружини = силі пружності при деформації, рівній одиниці (Н/м).Вільне коливання позначивши, отримуємо- лінійне однорідне рівняння другого порядку, характеристичне рівняння:, його корені мнимі, - загальне рішення диференційного рівняння буде:- постійні інтегрування. Для їх визначення знаходимо рівняння швидкостей:, представляємо початкові умови для, звідки

М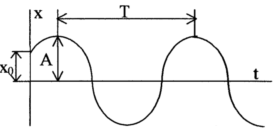ожна позначити- рівняння гармонічних коливань.амплітуда,початкова фаза вільних коливань;циклічна частота (кутова, власна) коливань, період:k та T не залежать від початкових умов – ізохронність коливань; амплітуда та початкова фаза залежать від початкових умов. Під дією постійної сили Р відбувається зміщення центру коливань в сторону дії сили Р на величину статичного відхиленняЯкщо Р – сила тяги, то.

Затихаючі коливання при дії сила опору, пропорційна швидкості (в’язке тертя)., позначившиотримуємо:, характеристичне рівняння:, його корені:.а)При n<k корені мнимі – загальне рішення диференційного рівняння має вигляд:

, позначивши

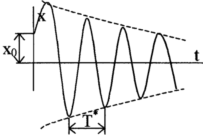Множник е^-nt показник, що коливання затухаюче.

Графік заключний поміж двома симетричними відносно вісі t кривими . З початкових умов:; частота затихаючих коливань:; період:, період затихаючих коливань більше періоду вільних коливань (при невеликих опорах). Амплітуди коливань зменшуються:- декремент коливальний;логарифмічний декремент; «n» - коефіцієнт затухання.

б) Аперіодичний рух точки при або. При n>k корені характеристичного рівняння речові, загальний розв’язок:позначаючи

- гіперболічні синус та косинус), якщо ввести ,то- це рівняння не коливального руху (аперіодичного), так як гіперболічний синус не являється періодичною функцією. При n=k корені характеристичного рівняння речові, рівні та негативні:загальний розв’язок:, або, рух також аперіодичний.

Вимушені коливання окрім відновлюючої сили діє змінна збурювальна сила, зазвичай, по гармонічному закону: - частота збурювальної сили, δ – початкова фаза.

- диференційне рівняння вимушених коливань (неоднорідне лінійне диференційне рівняння). Його загальний розв’язок = сумі загального розв’язку однорідного рівняння та частинного розв’язку даного рівняння:- частинний розв’язок, який мається у вигляді, подобному правій частині рівняння. Підставляючи розв’язок в рівняння, знаходимо:

. Величина статистичного відхилення: 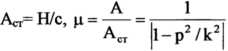- коефіцієнт динамічності, у скільки разів амплітуда коливань перебільшує статистичне відхилення. При-явище резонансу (частота здурювальної сили дорівнює частоті власних коливань, при цьому амплітуда безгранично зростає). При наступає явище, називаємебиттями: . Позначаючи, отримуємо- відбувається накладання додаткових коливань, визваних збурювальною силою, власно вимушені коливання – коливання частоти р, амплітуда яких являється періодичною функцією.Явище резонансу виникає при збіганні частот вимушених та вільних коливань точки p=k. Диференційне рівняння:

. Частинне рішення: тобто загальне рішення диференційного рівняння:Рівняння показує, що амплітуда вимушених коливань при резонансі зростає пропорційно часу. Період, фаза вимушених коливань відстає від фази здурю вальної сили на

Вимушені коливання при наявності тертя: загальне рішення в залежності від величини k та n: