I уровень

1.1.Докажите равенство:

1) 2)3)

4) 5)6)

1.2.Зная, чтодокажите равенство:

1) 2)

3) 4)

1.3.Докажите равенство:

1) 2)

II уровень

2.1. Проверив выполнение условий Д’Aламбера–Эйлера для функций и воспользовавшись одной из формулдокажите равенство:

1) 2)3)

2.2.Докажите равенство:

1) 2)

3) 4)

2.3.Решите уравнение:

1) 2)3)

III уровень

3.1.Дана функцияНайдите ее значения в указанных точках:

1)

2) где

29.5. Многозначные функции

Определим основные многозначные функции.

1.Функция где

При каждом z, (еслии) кореньимеетnразличных значений, которые задаются формулой

где (Для исключенных точек). Значит, функцияявляетсяn-значной.

2.Натуральный логарифм

Натуральный логарифм (логарифмическая функция) определяется равенством

(29.11)

где Это есть бесконечнозначная функция.

Главным значением логарифма Ln zназывают величину

(29.12)

Значит,

(29.13)

Справедливы формулы:

3.Степенная функция

Если тогдагдеВ этом случае– однозначная функция.

Если (m и n – взаимно-простые числа), то

причем, по определению

В этом случае –n-значная функция (при).

Если – произвольное комплексное число,причем(как во 2-м случае), то

В этом случае – бесконечнозначная функция.

4.Показательная функция

Эта функция определяется равенством

(29.14)

Функция есть бесконечнозначная функция.

5. Обратные тригонометрические функции

Обратные тригонометрические функции определяются равенствами:

Приведенные четыре обратные тригонометрические функции являются бесконечнозначными.

Главное значение логарифма используют для определения следующих функций:

(29.15)

из которых первые две – двузначные, а последние две – однозначные.

Пример 1. Вычислить:

1) 2)

Решение. 1) Воспользовавшись формулой (29.12), получаем

2) По формуле (29.11) находим

Пример 2. Выяснить, справедлива ли формула

Решение. Проверим справедливость формулы, например, для Согласно формуле (29.13), находим

Однако это не одно и то же. Если то из первого равенства получаем значениеТакое значение мы не можем получить из второго равенства ни при какомПриходим к выводу, что приведенная в условии формула не справедлива.

Пример 3. Вычислить: 1) 2)

Решение. 1) Воспользуемся формулой (29.14):

2) Вычисляем аналогично

Пример 3 показывает, что число 1 в иррациональной степени дает бесконечное множество комплексных значений. А все значения степени есть положительные действительные числа.

Пример 4. Вычислить:

1) 2)

Решение. 1) Согласно формуле (29.15), получаем

Записывая комплексное число в тригонометрической форме и извлекая квадратный корень, найдем два его значения, а именно:Значит,т. е. решение имеет два значения. Рассмотрим каждое из этих значений отдельно, воспользовавшись формулой (29.12):

Таким образом,

2) Вычислим последовательно:

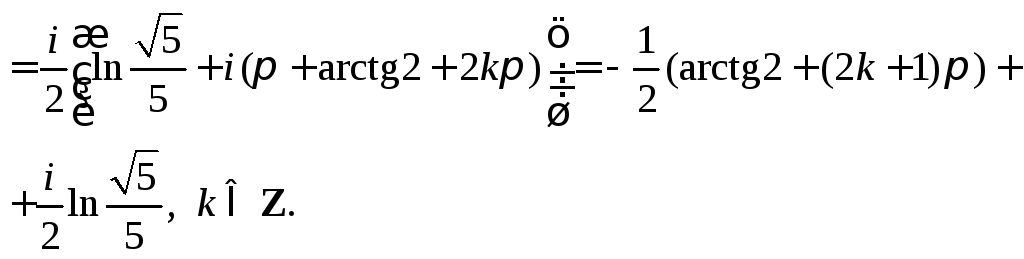
Задания

I уровень

1.1.Вычислите значение функции:

1) 2)3)

1.2.Вычислите значение функции:

1) 2)3)4)

II уровень

2.1.Докажите равенство:

1) 2)

2.2.Найдите ошибку в рассуждениях:

так как справедливо равенство

то, полагая в нем получаем

т. е.

с другой стороны,

2.3.Докажите равенствопроверив выполнение условий Д’Aламбера–Эйлера для функциии воспользовавшись формулой