I уровень

1.1.Найдите действительную и мнимую части функции:

1) 2)3)

1.2.Дано отображениеНайдите образ линии:

1) 2)

3) 4)

1.3.Найдите предел функции:

1) 2)

3) 4)

II уровень

2.1.Дано отображениеНайдите образ линии:

1) 2)

2.2.Найдите образ множества точек, заданного неравенствамипри отображении

2.3.Дано отображениеНайдите образ множества точек, ограниченного прямыми:

1) 2)3)

III уровень

3.1.Докажите, что функциянепрерывна при любом значении

1) 2) 3) 4)

3.2.Докажите, что:

1) 2)

3.3.Докажите, чтоне существует, если:

1) 2)

3.4.Дано отображениеНайдите:

1) длину образа отрезка

2) площадь образа замкнутой области

29.3. Дифференцирование функций

комплексной переменной

Пусть однозначная функция определена в некоторой окрестности точкиЕсли существует конечный пределто он называетсяпроизводной функции f(z) в точкеЕсли величинуназватьприращением аргумента в точке а величинуприращением функциив точкето можно дать эквивалентное определение производной, а именно:

Если функция f(z) имеет производную в точкето она называетсядифференцируемой в этой точке.

Функция f(z) дифференцируема в точкетогда и только тогда, когда для ее приращения выполняется равенство

где при

Дифференцируемая в точке функцияf(z) является непрерывной в этой точке. Функция f(z) называется дифференцируемой на множестве D, если она дифференцируема в каждой точке

Правила дифференцирования

Пусть все использованные в равенствах функции дифференцируемы в произвольной точке zнекоторого множества. Тогда:

1) где

2)

3) (29.3)

4)

5)

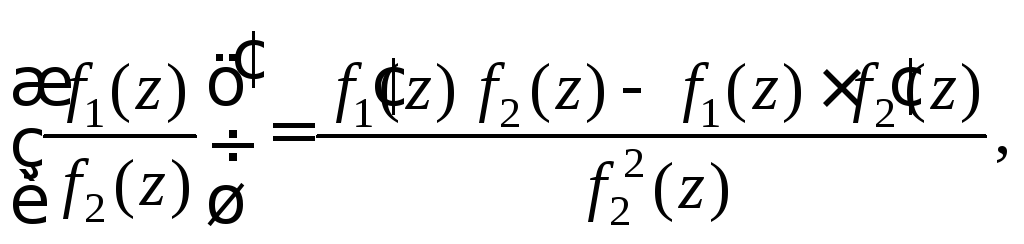
6) если то

7) если иесть обратная функция, то

,

Для дифференцируемой в точке zфункцииf(z) выполняется равенство

Величина называется дифференциалом функции f в точке z.

Справедливы формулы

Функция является дифференцируемой в точкетогда и только тогда, когда функцииu,vявляются дифференцируемыми в точке (x; y) и выполняются соотношения:

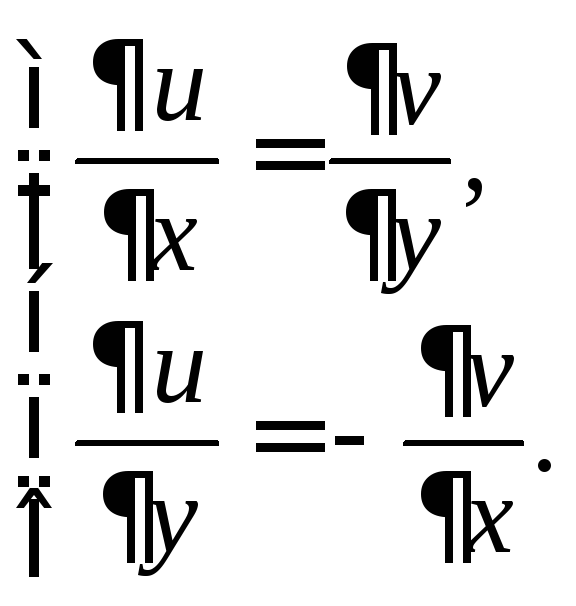(29.4)

Последние два равенства называют условиями Д’Аламбера–Эйлера (Коши–Римана).

Если все частные производные функций u,vнепрерывны в точке (x, y) и удовлетворяют условиям Д’Аламбера–Эйлера, то функцияявляется дифференцируемой в точке

Если функция f(z) является дифференцируемой в точкето для вычисления ее производной в этой точке справедливы формулы:

(29.5)

Геометрический смысл модуля производной: модуль производнойв точкеможно рассматривать как коэффициент растяжения в точкепри отображении

Геометрический смысл аргумента производной: аргумент производнойв точкеесть угол поворота касательной к кривой в точкепри отображении

Взаимно-однозначное отображение, которое сохраняет углы между кривыми, проходящими через некоторую точку, и дает одинаковый коэффициент их растяжения, называется конформным в этой точке.

Функция называетсяаналитической в области D, если она однозначна и дифференцируема в каждой точке этой области. Функцияf(z)называется аналитической в замкнутой области если существует областьв которой функция аналитична. Функция называетсяаналитической в точке, если существует некоторая окрестность этой точки, в которой функция аналитична.

Необходимыми и достаточными условиями аналитичности функции в областиDявляются дифференцируемость в областиDфункцийu,vи выполнение в этой области условий Д’Аламбера–Эйлера (29.4).

Однозначная функция u(x; y) двух действительных переменных называетсягармонической в области D, если она имеет непрерывные частные производные до второго порядка включительно и удовлетворяет уравнению Лапласа:

(29.6)

Действительная и мнимая части аналитической функции являются гармоническими функциями. Условие гармоничности функций u(x; y) и v(x; y) является необходимым условием аналитичности функции но не является достаточным.

Пусть D– произвольная область плоскостиĈ. Если для любой замкнутой линиикоторая принадлежит множествуD, внутренняя или внешняя область кривойцеликомпринадлежитD, то областьDназываетсяодносвязной.

Область, границей которой является объединение конечного числа замкнутых непрерывных непересекающихся кривых без точек самопересечения, называется многосвязной.Если граница области состоит изnуказанных кривых, то область называетсяn-связной.

Любая гармоническая в односвязной области Dфункция является действительной (мнимой) частью некоторой аналитической в областиDфункции. При этом вторая неизвестная часть этой функции находится с точностью до постоянного слагаемого по ее известной части.

Пример 1. Выяснить, дифференцируема ли функция

Решение. Находим т. е. Проверим, выполняются ли условия (29.4) дифференцируемости функции.

Вычисляем

Видим, что условие выполняется приа условие– приТаким образом, сразу оба условия Д’Aламбера–Эйлера не выполняются ни в одной точке комплексной плоскости, т. е. функция не является дифференцируемой ни в одной точке.

Пример 2. Выяснить дифференцируемость функции f(z) и найти ее производную, если:

1) 2)

Решение. 1) 1-й способ. Функция определена в каждой точке плоскости C. Найдем ее действительную часть u, а также мнимую часть v.

т. е. Проверим, имеет ли эта функция непрерывные частные производные. Найдем их:

Видим, что все производные непрерывны на плоскости C и удовлетворяют на ней условиям Коши–Римана (29.4). Значит, функция f(z) является дифференцируемой на всей комплексной плоскости. Для вычисления ее производной можно использовать, например, формулу (29.5):

2-й способ. Используя формулу и правила дифференцирования (29.3), получимОчевидно, что этот способ нахождения производной рациональнее, чем первый.

2) Функция определена на всей плоскости C. Найдем ее действительную и мнимую части, преобразовав выражение, которым она задается (при условии ):

Тогда

Частные производные непрерывны всюду на множестве C, но нельзя утверждать, что условия Коши–Римана выполняются для всех Найдем те точки, где они справедливы, т. е. где имеет решение система

Поскольку она равносильна системе

то видим, что условия Коши–Римана выполняются только в точке (0; 0). Для этой точки все частные производные равны нулю, значит,

Пример 3. Найти коэффициент растяжения и угол поворота при отображении в точке

Решение.

Откуда получаем коэффициент растяжения в заданной точке:

Находим угол поворота для заданного отображения:

Пример 4. Найти область аналитичности функции:

1) 2)3)

Решение. 1) Поскольку то

Тогда

Условия Д’Аламбера–Эйлера (29.4) выполняются в единственной точке В этой точке функция является дифференцируемой, но не является аналитической. Таким образом, функцияне является аналитической ни в одной точке комплексной плоскости.

2) Найдем действительную и мнимую части заданной функции:

т. е.

Находим частные производные:

Условия Д’Aламбера–Эйлера (29.4) выполняются во всех точках, кроме точки Функцияаналитична на всей комплексной плоскости, кроме точки

3) Для нахождения действительной и мнимой частей заданной функции используем формулы Эйлера:

Поэтому

Вычисляем

Замечаем, что условия дифференцируемости (29.4) выполняются для всех т. е. функцияаналитична на всей комплексной плоскости.

Пример 5. Восстановить аналитическую функцию f(z) по ее известной части (если это возможно): 1) действительной 2) мнимой3) действительной

Решение. 1) Убедимся, что функция u(x, y) является гармонической. Поскольку

и то справедливо равенство (29.6). Первое равенство из условий Коши–Римана (т. е. ) приобретает видоткуда после интегрирования имеем

Таким образом, приходим к выражению

Из второго равенства Коши–Римана имеем:или, то же самое,

Из последнего равенства получаем и соответственноВ результате найдена функцияи восстановлена аналитическая функция

которую можно записать иначе:

Это то же самое, что

2) Нетрудно убедиться, что функция v(x, y) является гармонической, так как

Равенство из условий Коши–Римана принимает видИнтегрируя его, находим

Второе равенство из тех же условий дает

Значит,

Из последнего равенства получаем и соответственно

Таким образом, и

Функцию f(z) можно записать в виде зависимости от z. Действительно,

что приводит к виду

3) Проверим, является ли функция гармонической. Вычислим соответствующие частные производные:

Уравнение Лапласа (29.6) для этой функции приобретает вид откуда видим, что функция удовлетворяет уравнению Лапласа только в точках прямойПриходим к заключению, что она не является гармонической, так как не существует области, в которой справедливо равенство (29.6). По этой причине не существует аналитической функции, у которой действительная часть есть

Задания