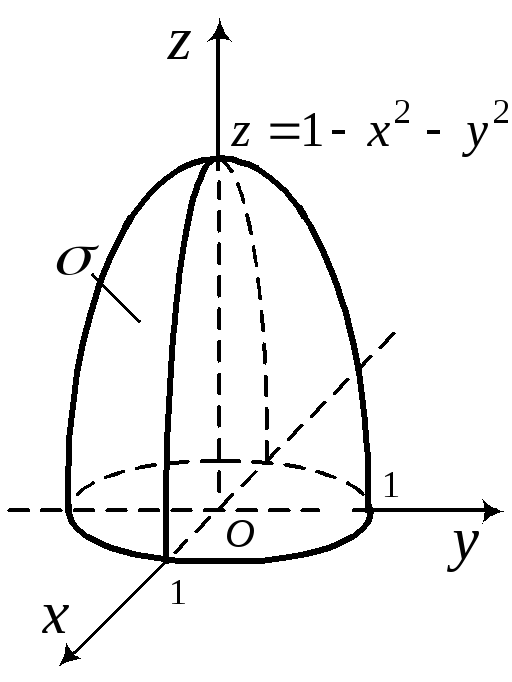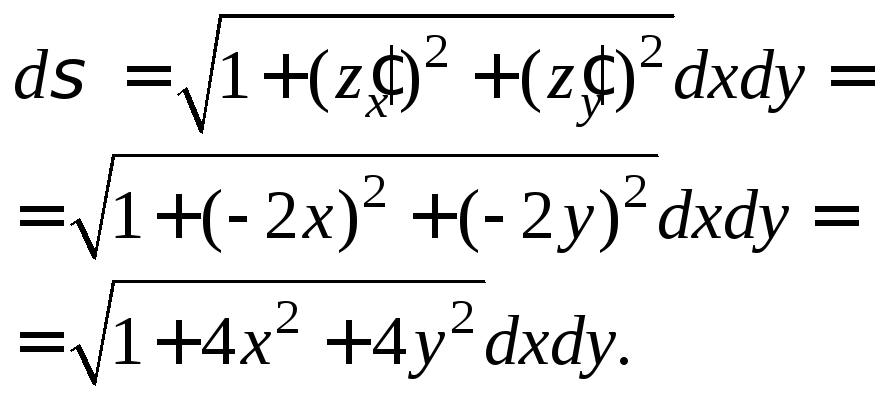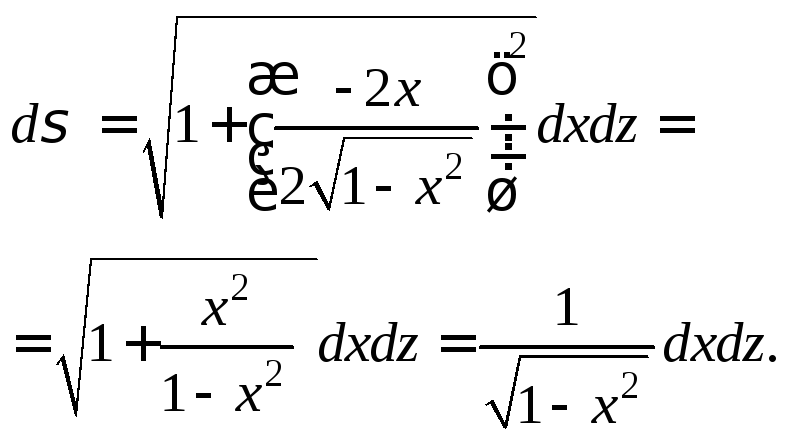27. Поверхностные интегралы. Элементы

ТЕОРИИ ПОЛЯ

27.1. Поверхностный интеграл 1-го рода

Пусть функция f(x; y; z) непрерывна на некоторой гладкой замкнутой ограниченной поверхности Разобьем эту поверхность произвольным образом на элементарные поверхностиплощади которых будем считать соответственно равнымиВнутри каждой элементарной области выберем произвольную точку

Диаметром ограниченной замкнутой поверхности будем называть наибольшее расстояние между любыми двумя точками границы поверхности. Обозначим через диаметры элементарных поверхностейа через– максимальный диаметр, т. е.Составим интегральную сумму

Устремим так, чтобыЕсли существует предел последовательности интегральных сумм, который не зависит ни от способа разбиения поверхностини от выбора точек то этот предел называетсяповерхностным интегралом 1-го рода от функции f(x; y; z) по поверхности

При этом говорят, что функция f(x; y; z) интегрируема на поверхности x, y и z называют переменными интегрирования.

Достаточное условие интегрируемости функции: если определенная на некоторой ограниченной замкнутой гладкой поверхности функция непрерывна, то она интегрируема на этой поверхности.

Если функции f(x; y; z), f₁(x; y; z) и f₂(x; y; z) интегрируемы на поверхности то имеют место следующие свойства:

1) линейность:

где

2) аддитивность:

причем поверхности ₁ и ₂ не имеют общих внутренних точек;

3) если для любой точки выполняется неравенството

4) оценка модуля интеграла:

5) если то

где S – площадь ограниченной части поверхности .

Геометрический смысл поверхностного интеграла 1-го рода:

где S – площадь поверхности .

Физический смысл поверхностного интеграла 1-го рода:

если f(x; y; z) – поверхностная плотность материальной поверхности , то

(27.1)

где m – масса поверхности .

Пусть f(x; y; z) – функция, непрерывная в точках поверхности . Вычисление поверхностного интеграла 1-го рода сводится к вычислению двойного интеграла. В зависимости от способа задания поверхности  и ее функции возможны следующие случаи вычисления поверхностного интеграла 1-го рода:

1. Если поверхность задана явно уравнениеми однозначно проектируется на областьплоскостиxOy, то

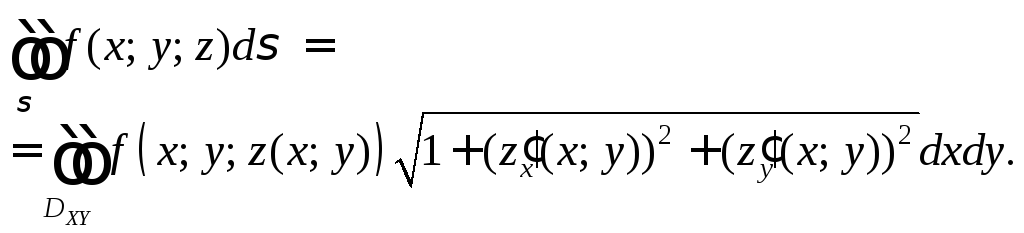(27.2)

2. Если поверхность задана явно уравнениеми однозначно проектируется на областьплоскостиxOz, то

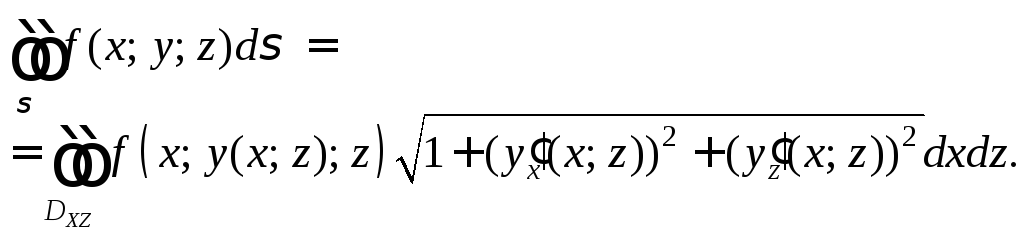(27.3)

3. Если поверхность задана явно уравнениеми однозначно проектируется на областьплоскостиyOz, то

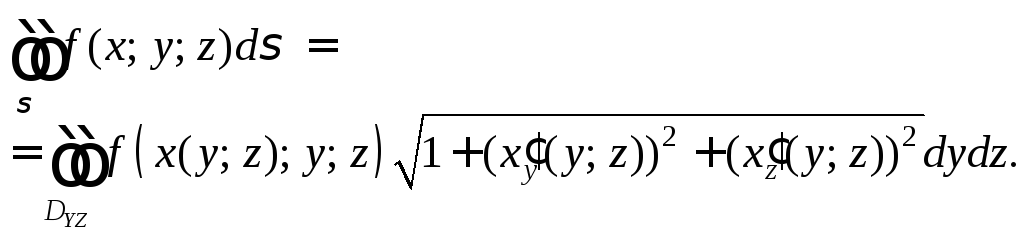(27.4)

4. Если поверхность задана неявно уравнениемкоторое определяет единственную функциюто

(27.5)

где D – проекция поверхности на плоскостьxOy, на всей поверхности

Координаты центра масс материальной поверхности с поверхностной плотностью распределения масс, выражаемой функциейf(x, y, z), находятся по формулам:

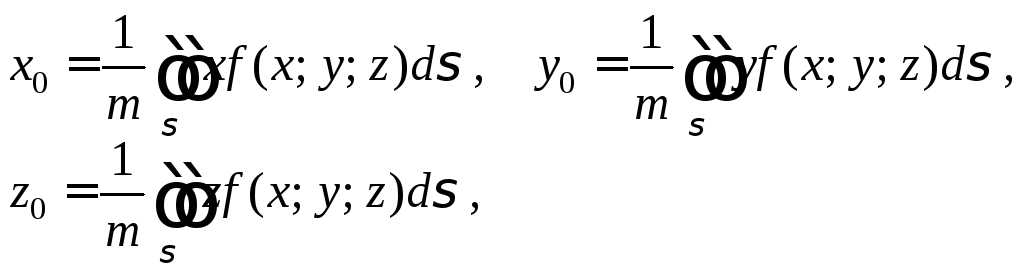(27.6)

где m – масса поверхности рассчитываемая по формуле (27.1).

Пример 1. Вычислить поверхностный интеграл 1-го рода по поверхности , ограниченной указанными поверхностями:

1)

2)

Решение. 1) Определим поверхность , заключенную между круговым параболоидом и плоскостьюxOy (рис. 27.1).

Рис. 27.1

Проекция этой поверхности на плоскость xOy будет представлять собой круг с центром в начале координат радиуса 1, т. е. Для вычисления поверхностного интеграла 1-го рода применим формулу (27.2). Вначале найдем элемент площади

Для вычисления поверхностного интеграла подставим полученное выражение в указанную формулу и осуществим переход к двойному интегралу по области D_XY. Получим:

По формулам в подынтегральном выражении перейдем к полярным координатам и найдем полученный повторный интеграл:

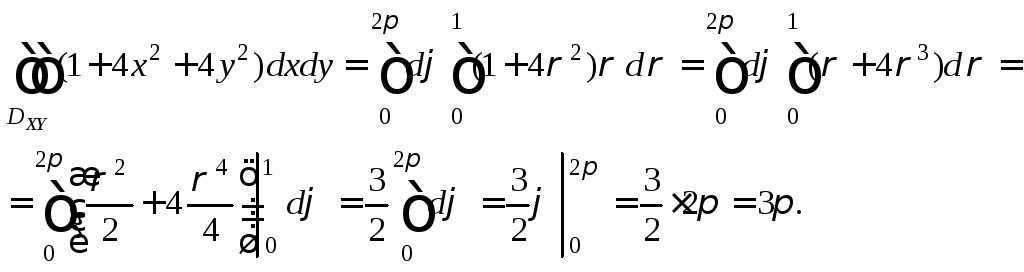
2) Поверхность ограничена частью цилиндрической поверхности между плоскостямии(рис. 27.2). Ее проекцией на плоскостьxOy будет являться прямоугольник

Рис. 27.2

По формуле предварительно рассчитаем элемент площади

Для вычисления поверхностного интеграла применим формулу (27.3) и учтем, что явное задание поверхности имеет вид: Получим двойной интеграл:

Перейдя к повторному интегралу, вычислим его интеграл:

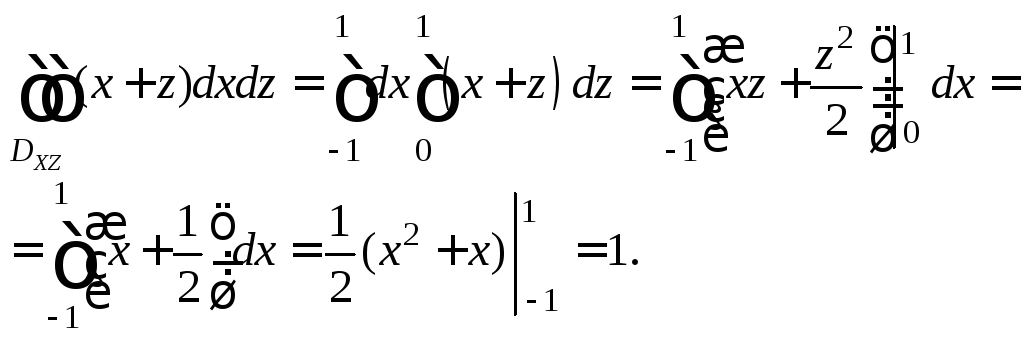
Пример 2. Вычислить интеграл где – часть поверхности отсекаемая плоскостямии

Решение. Поверхность представляет собой часть конуса вдоль осиOx, ограниченную плоскостями и(рис. 27.3).

Рис. 27.3

Мы имеем дело с неявным заданием поверхности уравнениемПоэтому целесообразно применить формулу, аналогичную соотношению (27.5). Вначале вычислим элемент площади, применив формулу В нашем случае

Так как откудаимеем

Перейдем к двойному интегралу, применив формулу (27.5) и подставив найденный элемент площади:

Учтем, что проекцией поверхностина плоскостьyOz является кольцо между окружностями иДалее целесообразно перейти к полярным координатам с помощью соотношенийгдеПолучим повторный интеграл и вычислим его:

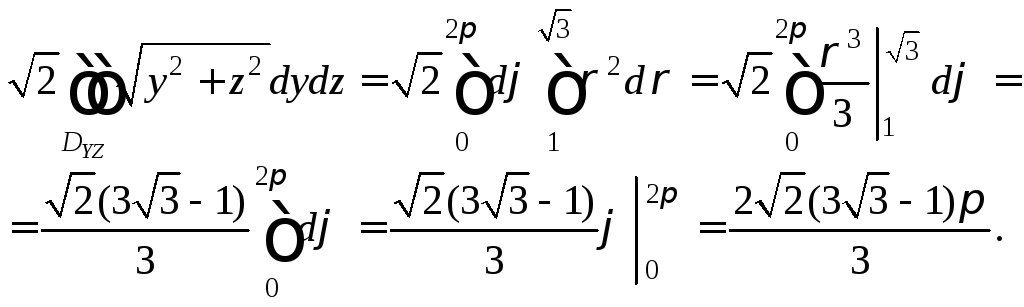
Пример 3. Используя поверхностный интеграл 1-го рода, найти координаты центра масс поверхности ограниченной поверхностямиипри условии, что поверхностная плотность распределения масс выражается функцией

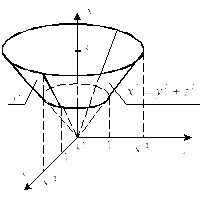
Решение. Уравнение задает часть конуса вдоль осиOz при отсекаемую плоскостью(рис. 27.4).

Найдем массу этой части конуса по формуле (27.1):

Спроектировав ограниченную поверхность конуса на плоскость xOy, получим круг По формуламперейдем к полярным координатам, причем в нашем случаеПрименив формулувычислим элемент площади

Поверхностный интеграл 1-го рода вычислим по формуле (27.2):

Рис. 27.4

Абсциссу, ординату и аппликату центра масс находим по формулам (27.6). Учтем также, что элемент площади в декартовых координатах при переходе к полярным координатам приобретает вид:Получим следующие соотношения:

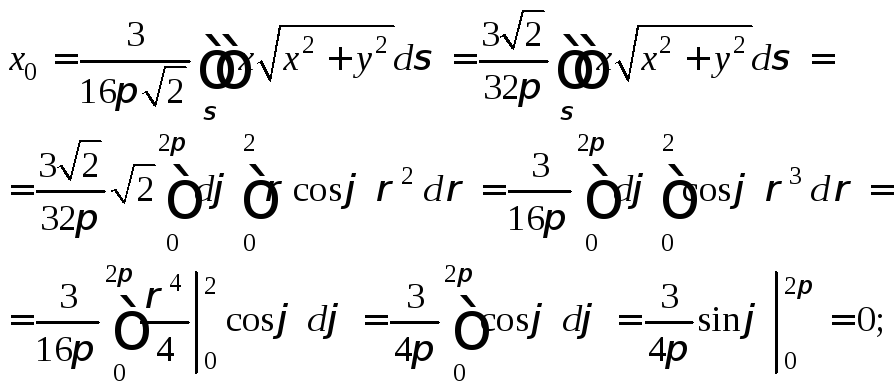
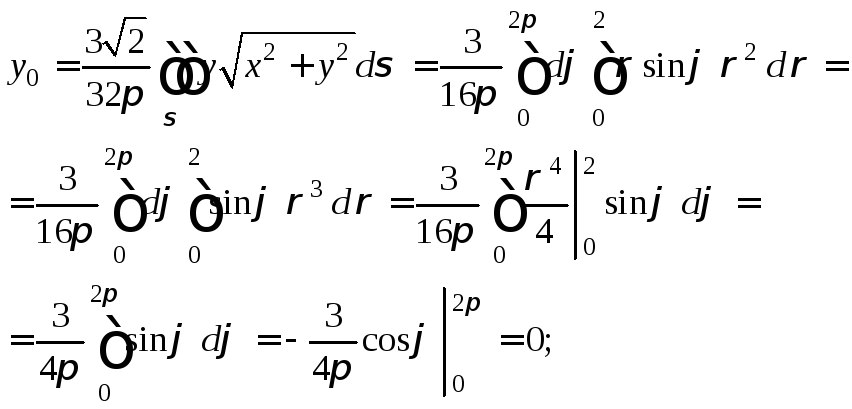
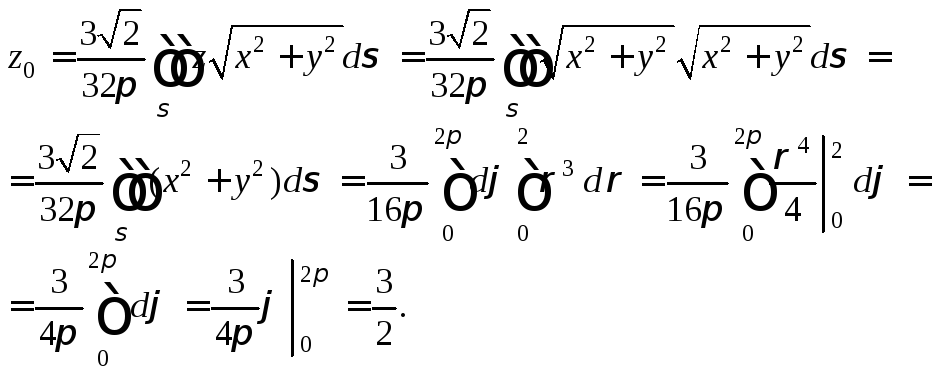
Итак, центр масс находится в точке (0; 0; 1,5).

Задания