I уровень
1.1. Вычислите поверхностный интеграл 2-го рода:
1)
![]() где
где
![]() – верхняя часть плоскости
– верхняя часть плоскости
![]() расположенная в первом октанте;
расположенная в первом октанте;
2)
![]() где
где
![]() – внешняя сторона поверхности параболоида
– внешняя сторона поверхности параболоида
![]() отсекаемая плоскостью
отсекаемая плоскостью![]()
1.2. С помощью формулы Остроградского–Гаусса вычислите поверхностный интеграл:
1) ![]() где
где
![]() – внешняя сторона поверхности куба,
ограниченного плоскостями
– внешняя сторона поверхности куба,
ограниченного плоскостями
![]()
![]()
![]()
![]()
![]()
![]()
2) ![]() где
где
![]() – внешняя сторона цилиндра
– внешняя сторона цилиндра
![]() с основаниями
с основаниями![]() и
и![]()
II уровень
2.1. Вычислите поверхностный интеграл 2-го рода:
1)
![]() где
где
![]() – верхняя часть плоскости
– верхняя часть плоскости
![]() расположенная в первом октанте;
расположенная в первом октанте;
2)
![]() где
где
![]() – внешняя часть поверхности гиперболоида
– внешняя часть поверхности гиперболоида
![]() отсекаемая плоскостями
отсекаемая плоскостями![]()
![]()
3)
![]() где
где
![]() – внешняя часть поверхности
– внешняя часть поверхности
![]() отсекаемая плоскостью
отсекаемая плоскостью![]()
4)
![]() где
где
![]() – внешняя сторона поверхности эллипсоида
– внешняя сторона поверхности эллипсоида
![]() расположенная в первом октанте.
расположенная в первом октанте.
2.2. С помощью формулы Остроградского–Гаусса вычислите поверхностный интеграл:
1)
![]() где
где
![]() – внутренняя сторона замкнутой
поверхности, образованной конусом
– внутренняя сторона замкнутой
поверхности, образованной конусом
![]() и плоскостью
и плоскостью![]()
2)
![]() где
где
![]() – внешняя часть поверхности тела,
ограниченной поверхностями
– внешняя часть поверхности тела,
ограниченной поверхностями
![]() и
и![]()
III уровень
3.1. Вычислите поверхностный интеграл 2-го рода:
1)
![]() где
где
![]() – верхняя часть плоскости
– верхняя часть плоскости
![]() расположенная в первом октанте;
расположенная в первом октанте;
2)
![]() где
где
![]() – внешняя сторона нижней половины сферы
– внешняя сторона нижней половины сферы
![]()
3)
![]() где
где
![]() – внешняя часть поверхности параболоида
– внешняя часть поверхности параболоида
![]() отсекаемая плоскостью
отсекаемая плоскостью![]()
4)
![]() где
где
![]() – наружная поверхность цилиндра
– наружная поверхность цилиндра
![]() отсекаемая плоскостями
отсекаемая плоскостями![]()
![]()
![]()
3.2. С помощью формулы Остроградского–Гаусса вычислите поверхностный интеграл:
1) ![]() где
где
![]() – внешняя сторона сферы
– внешняя сторона сферы
![]()
2)
![]() где
где
![]() – внешняя часть поверхности тела,
ограниченного поверхностями
– внешняя часть поверхности тела,
ограниченного поверхностями
![]()
![]()
![]()
27.3. Элементы теории поля
Если
каждой точке
![]() поставлена в соответствие некоторая
скалярная величина
поставлена в соответствие некоторая
скалярная величина![]() то говорят, что в областиV
пространства
то говорят, что в областиV
пространства
![]() заданоскалярное
поле
заданоскалярное
поле
![]() Если функция
Если функция![]() не зависит от времени, то скалярное поле
называетсястационарным;
поле, меняющееся с течением времени, –
нестационарным.
Далее будем рассматривать только
стационарные поля.
не зависит от времени, то скалярное поле
называетсястационарным;
поле, меняющееся с течением времени, –
нестационарным.
Далее будем рассматривать только
стационарные поля.
Скалярное
поле можно изображать графически в виде
поверхностей
уровня –
множества точек (x; y; z),
в которых функция принимает постоянное
значение
![]() Если заданная функция
Если заданная функция![]() является непрерывной и дифференцируемой
в областиV,
то через каждую точку, не являющуюся
критической, проходит единственная
поверхность уровня.
является непрерывной и дифференцируемой
в областиV,
то через каждую точку, не являющуюся
критической, проходит единственная
поверхность уровня.
В
случае задания функции двух переменных
![]()
![]() рассматриваемое скалярное поле называетсяплоским,
а множество точек (x; y),
в которых
рассматриваемое скалярное поле называетсяплоским,
а множество точек (x; y),
в которых
![]() называется
линиями уровня.
называется
линиями уровня.
Для
характеристики скорости изменения поля
![]() в заданном направлении вводится такая
характеристика, как производная от
функции по направлению (см. Математика
в примерах и задачах. Ч. 3, с. 266), физический
смысл которой состоит в том, что модуль
данной производной представляет собой
мгновенную скорость изменения функции
в направлении дифференцирования в
выбранной точке. С физической точки
зрения направление наибыстрейшего
возрастания функции задает градиент
функции (см. там же.).
в заданном направлении вводится такая
характеристика, как производная от
функции по направлению (см. Математика
в примерах и задачах. Ч. 3, с. 266), физический
смысл которой состоит в том, что модуль
данной производной представляет собой
мгновенную скорость изменения функции
в направлении дифференцирования в
выбранной точке. С физической точки
зрения направление наибыстрейшего
возрастания функции задает градиент
функции (см. там же.).
Если
каждой точке
![]() поставлен в соответствие некоторый
вектор
поставлен в соответствие некоторый
вектор![]() то говорят, что в области
то говорят, что в области![]() задановекторное
поле
задановекторное
поле
![]() Задание векторного поля
Задание векторного поля![]() равносильно заданию вектор-функции
равносильно заданию вектор-функции
![]() (27.12)
(27.12)
В случае отсутствия одной из переменных x, y, z, или равенства нулю одной из функций P(x; y; z), Q(x; y; z), R(x; y; z), рассматриваемое векторное поле является плоским.
Если
в каждой точке области существуют все
непрерывные частные производные первого
порядка от функций P(x; y; z),
Q(x; y; z)
и R(x; y; z),
векторное поле (27.12) называется
дифференцируемым
в области
V.
По аналогии со скалярным полем, если
вектор
![]() не зависит от времени, задаваемое им
векторное поле называетсястационарным;
поле, меняющееся с течением времени, –
нестационарным.
не зависит от времени, задаваемое им
векторное поле называетсястационарным;
поле, меняющееся с течением времени, –
нестационарным.
Геометрическими
характеристиками векторного поля
![]() являютсявекторные
линии,
т. е. линии, касательные к которым в
каждой точке имеют направление вектора
являютсявекторные
линии,
т. е. линии, касательные к которым в
каждой точке имеют направление вектора
![]()
Пусть векторное поле образовано вектором (27.12), который будем считать вектором скорости некоторого потока несжимаемой жидкости, движущейся стационарно. Предположим, что в этом потоке находится некоторая поверхность , пропускающая данную жидкость.
Потоком
вектора
![]() через
поверхность
называется интеграл по поверхности
от скалярного произведения вектора
поля
через
поверхность
называется интеграл по поверхности
от скалярного произведения вектора
поля
![]() на единичный вектор
на единичный вектор![]() нормали к поверхности, т. е. поверхностный
интеграл 1-го рода
нормали к поверхности, т. е. поверхностный
интеграл 1-го рода
![]()
С учетом формулы (27.8) при вычислении потока вектора через поверхность можно легко перейти к поверхностному интегралу 2-го рода
![]() (27.13)
(27.13)
С
физической точки зрения поток вектора
![]() представляет собой скалярную величину,
численно равную объему несжимаемой
жидкости, протекающей через поверхность
за единицу времени.
представляет собой скалярную величину,
численно равную объему несжимаемой
жидкости, протекающей через поверхность
за единицу времени.
Если поверхность является замкнутой и ограничивает некоторый объем V, поток вектора записывают в виде
![]()
причем
за направление вектора
![]() принято брать направление внешней
нормали, тогда поток считается идущим
изнутри поверхности.
В этом случае величина потока K
через замкнутую поверхность выражает
разность между количеством жидкости,
вытекающей из области объема V
и втекающей в нее за единицу времени.
При этом, если
принято брать направление внешней
нормали, тогда поток считается идущим
изнутри поверхности.
В этом случае величина потока K
через замкнутую поверхность выражает
разность между количеством жидкости,
вытекающей из области объема V
и втекающей в нее за единицу времени.
При этом, если
![]() из областиV
вытекает больше жидкости, чем в нее
втекает, т. е.
внутри области имеются дополнительные
источники. При
из областиV
вытекает больше жидкости, чем в нее
втекает, т. е.
внутри области имеются дополнительные
источники. При
![]() внутри областиV
имеются стоки, поглощающие избыток
жидкости. Значение потока
внутри областиV
имеются стоки, поглощающие избыток
жидкости. Значение потока
![]() свидетельствует о том, что из областиV
вытекает столько же жидкости, сколько
и втекает в нее за единицу времени, т. е.
внутри рассматриваемой области либо
нет источников и стоков, либо их действие
взаимно компенсируется.
свидетельствует о том, что из областиV
вытекает столько же жидкости, сколько
и втекает в нее за единицу времени, т. е.
внутри рассматриваемой области либо
нет источников и стоков, либо их действие
взаимно компенсируется.
Для
описания распределения и интенсивности
источников и стоков векторного поля
применяют такую характеристику, как
дивергенция. Дивергенцией
векторного
поля
![]() в точкеM(x; y; z)
называется предел отношения потока
поля через замкнутую поверхность ,
окружающую точку M,
к объему V
тела, ограниченного этой поверхностью,
при стремлении диаметра этого тела
в точкеM(x; y; z)
называется предел отношения потока
поля через замкнутую поверхность ,
окружающую точку M,
к объему V
тела, ограниченного этой поверхностью,
при стремлении диаметра этого тела
![]() к нулю:
к нулю:
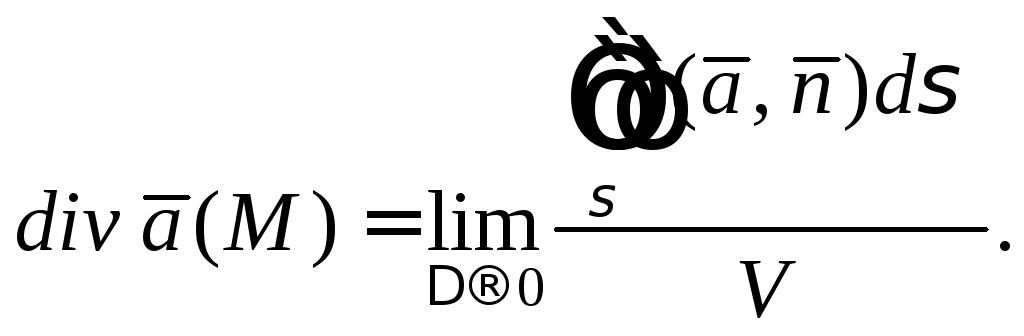
Если
векторное поле
![]() дифференцируемо в областиV,
то в любой точке M(x; y; z)
существует дивергенция поля, причем
дифференцируемо в областиV,
то в любой точке M(x; y; z)
существует дивергенция поля, причем
![]() (27.14)
(27.14)
Физический
смысл дивергенции состоит в том, что
абсолютная величина
![]() выражает интенсивность источника или
стока в токеM.
По знаку дивергенции можно судить о
наличии источника или стока векторного
поля в рассматриваемой точке M:
если
выражает интенсивность источника или
стока в токеM.
По знаку дивергенции можно судить о
наличии источника или стока векторного
поля в рассматриваемой точке M:
если ![]() то в точке M
находится источник; если
то в точке M
находится источник; если ![]() в точке M
– сток; при
в точке M
– сток; при ![]() источников и стоков в точке M
нет.
источников и стоков в точке M
нет.
Cвойства дивергенции:
если
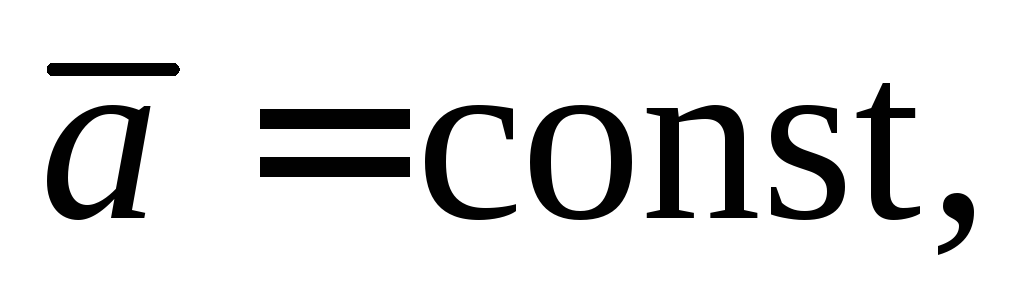 то
то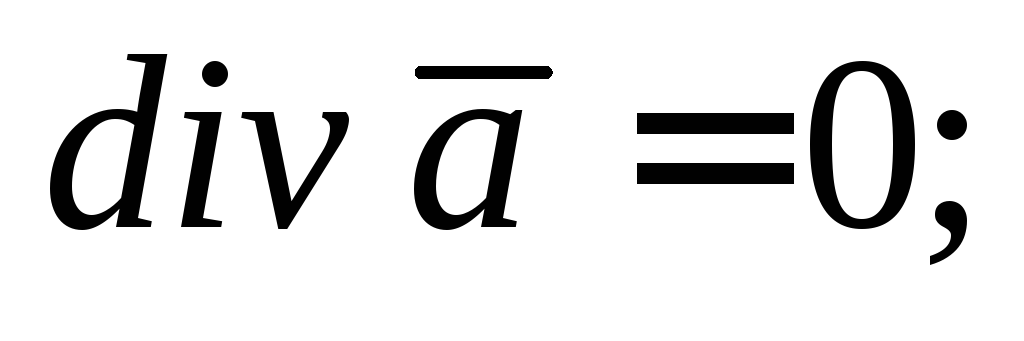
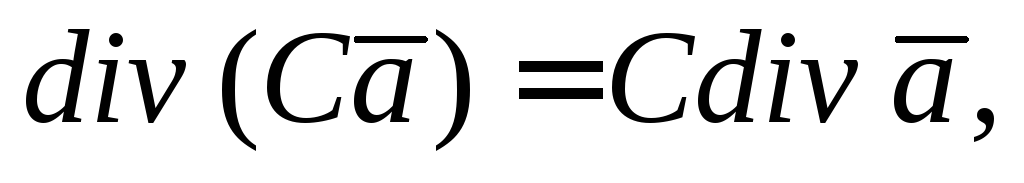 где
где
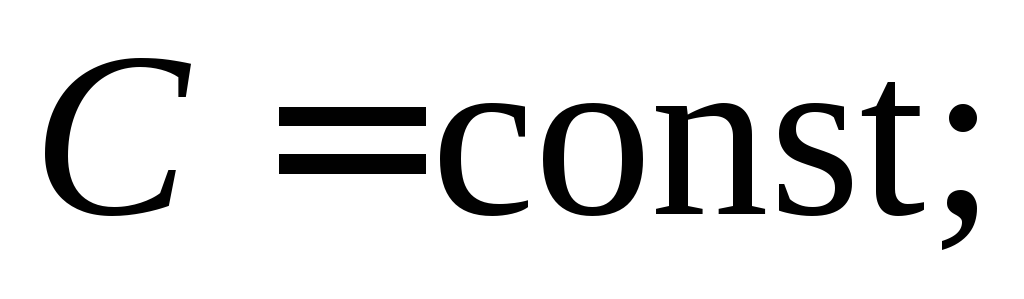
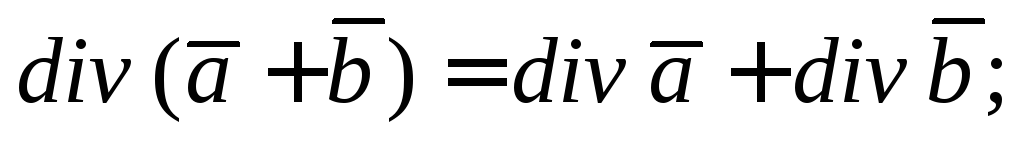
если u является скалярной функцией, то
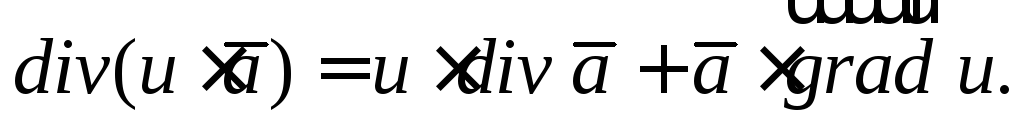
Формулу Остроградского–Гаусса (27.11) можно записать в векторном виде
![]()
Пусть
в области
![]() задано векторное поле (27.12) и гладкая
поверхность
задано векторное поле (27.12) и гладкая
поверхность![]() с границейL,
причем функции P(x; y; z),
Q(x; y; z)
и R(x; y; z)
являются непрерывно дифференцируемыми,
а обход контура – положительным.
с границейL,
причем функции P(x; y; z),
Q(x; y; z)
и R(x; y; z)
являются непрерывно дифференцируемыми,
а обход контура – положительным.
Циркуляцией
векторного поля
![]() вдоль контураL
называется криволинейный интеграл
вдоль контураL
называется криволинейный интеграл
![]() (27.15)
(27.15)
где
![]() – единичный вектор, направленный по
касательной к кривойL
в направлении ее обхода.
– единичный вектор, направленный по
касательной к кривойL
в направлении ее обхода.
Физический
смысл циркуляции состоит в том, что если
замкнутая кривая L
расположена в силовом поле
![]() то циркуляция равна работе силы
то циркуляция равна работе силы![]() при перемещении материальной точки
вдольL
(см. формулу (26.14)).
при перемещении материальной точки
вдольL
(см. формулу (26.14)).
Ротором
векторного поля
![]() в точкеM(x; y; z)
называется предел отношения при
стягивании контура L
в точку M:
в точкеM(x; y; z)
называется предел отношения при
стягивании контура L
в точку M:
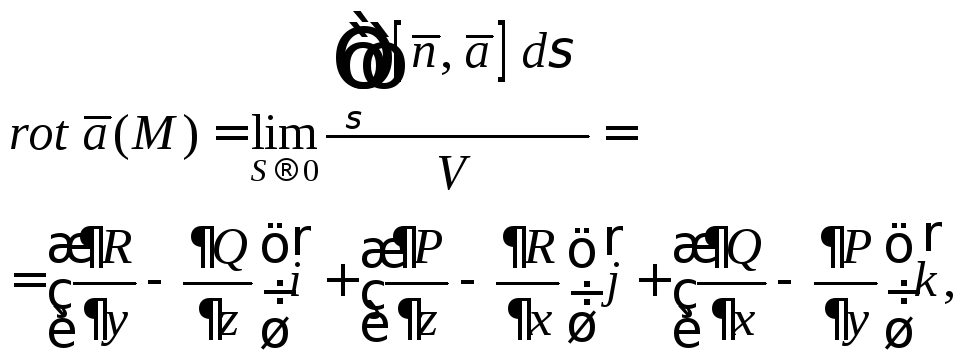 (27.16)
(27.16)
где
![]() – вектор нормали к замкнутой поверхности
– вектор нормали к замкнутой поверхности![]() в точкеM,
в точкеM,
V – объем области,
S – площадь поверхности интегрирования.
Свойства ротора:
если
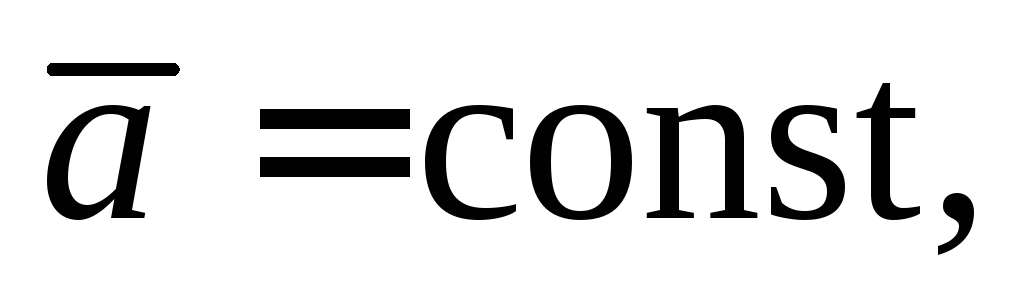 то
то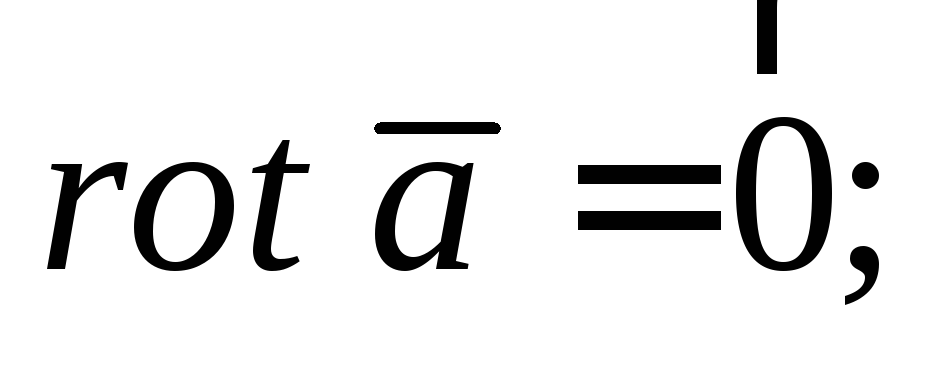
если
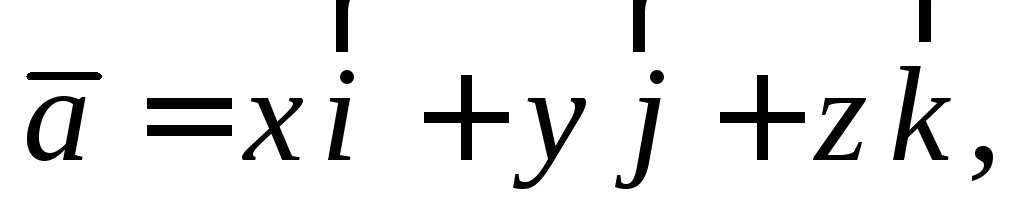 то
то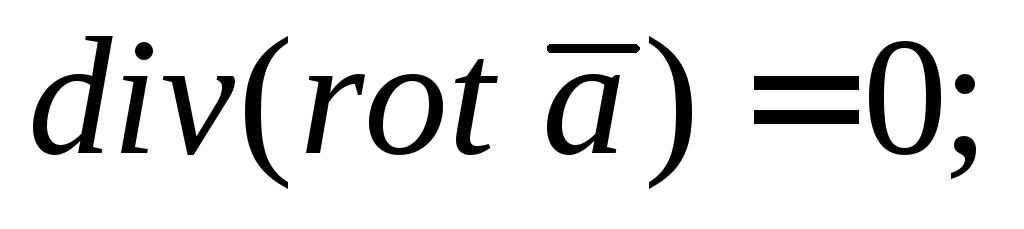
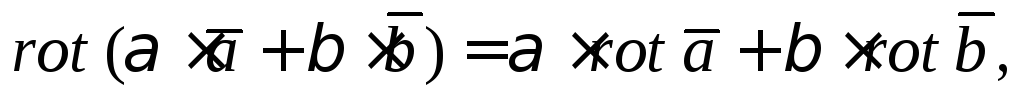 где
где
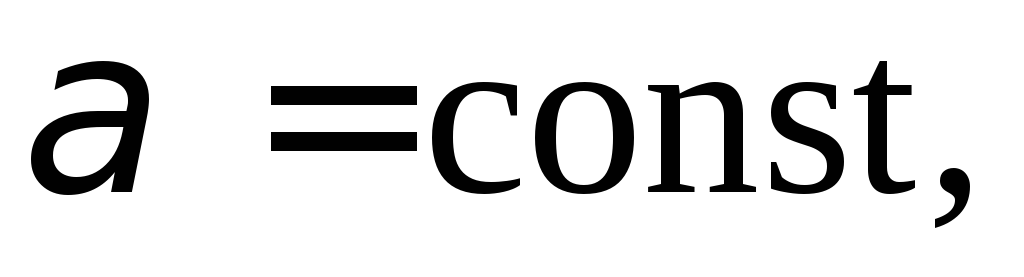
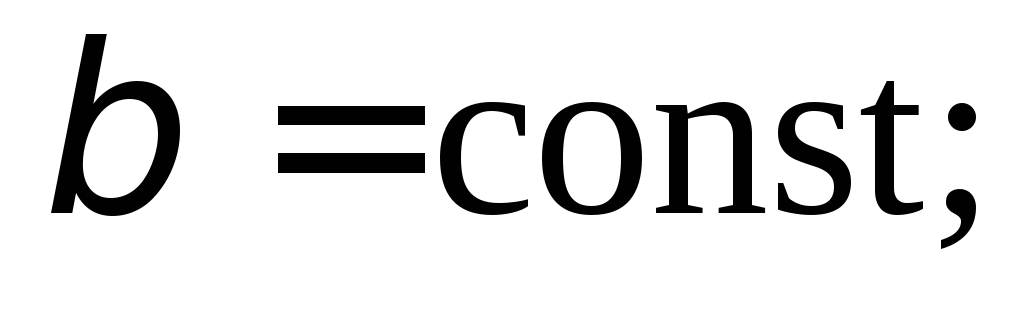
если u представляет собой скалярную функцию, то
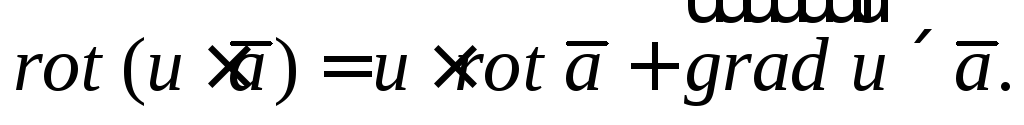
Формулу (27.16) можно записать в символической форме:
 (27.17)
(27.17)
С
физической точки зрения направление
ротора – это направление, вокруг которого
циркуляция имеет наибольшую плотность
по сравнению с циркуляцией вокруг любого
направления, не совпадающего с нормалью
к поверхности
![]()
Имеет место соотношение
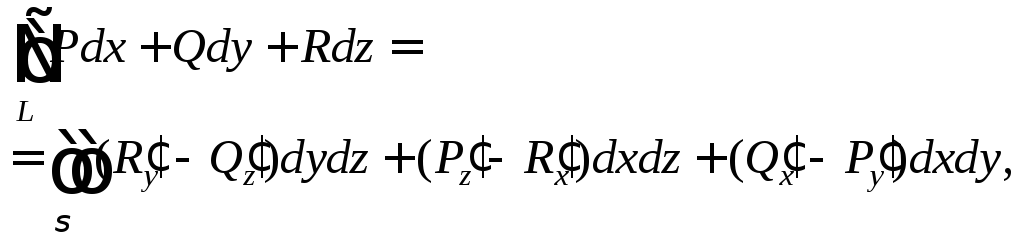
называемое формулой Стокса. Эта формула может быть записана в векторном виде
![]() (27.18)
(27.18)
где
левая часть соотношения представляет
собой циркуляцию вектора
![]() по контуруL,
а правая часть – поток вектора
по контуруL,
а правая часть – поток вектора
![]() через поверхность
через поверхность
![]() ограниченную контуром L.
Таким образом, формула Стокса (27.18)
показывает, что циркуляция вектора
ограниченную контуром L.
Таким образом, формула Стокса (27.18)
показывает, что циркуляция вектора
![]() вдоль замкнутого контураL
равна потоку ротора этого вектора
вдоль замкнутого контураL
равна потоку ротора этого вектора
![]() через поверхность, лежащую в этом
векторном поле и ограниченную контуромL.
через поверхность, лежащую в этом
векторном поле и ограниченную контуромL.
Векторное
поле, в каждой точке
![]() которого дивергенция поля равна нулю,
т. е.
которого дивергенция поля равна нулю,
т. е.
![]() называется
соленоидальным
в области V.
Для соленоидального поля в области V
характерно следующее:
называется
соленоидальным
в области V.
Для соленоидального поля в области V
характерно следующее:
нет источников и стоков;
для любой замкнутой поверхности
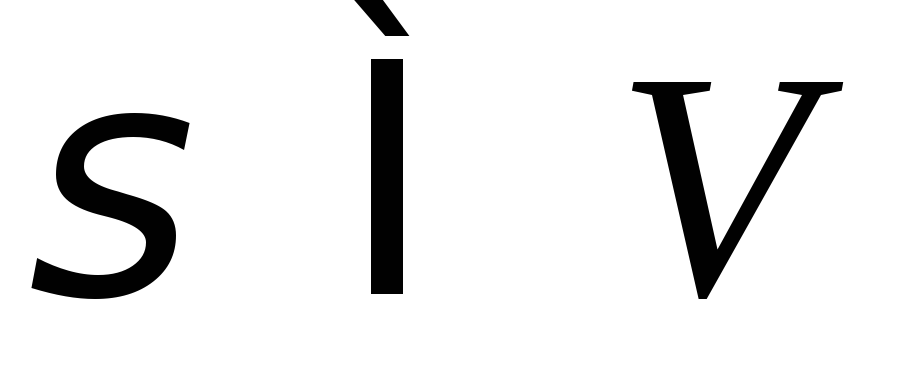 поток векторного поля через поверхность
поток векторного поля через поверхность
 равен нулю;
равен нулю; векторные линии поля являются замкнутыми или имеют концы на границе области V.
Если
в каждой точке векторного поля
![]()
![]() выполняется соотношение
выполняется соотношение![]() векторное
поле называется потенциальным
в области V
задания поля.
векторное
поле называется потенциальным
в области V
задания поля.
Согласно определению ротора (27.16), необходимым и достаточным условием потенциальности поля является справедливость равенств:
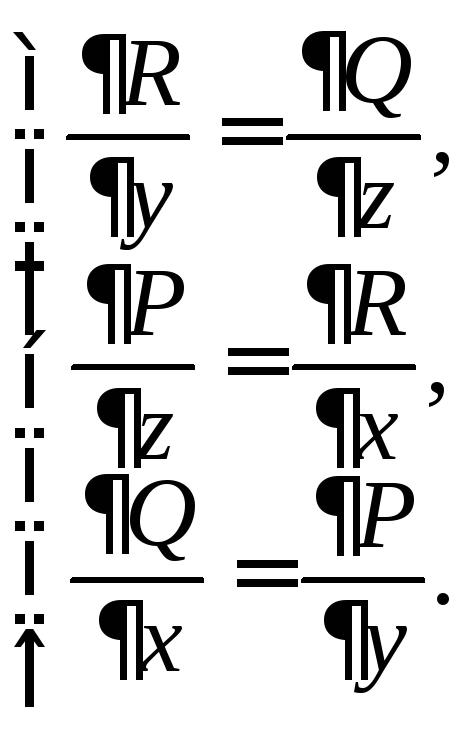 (27.19)
(27.19)
Для
того чтобы поле
![]() было потенциальным в областиV,
необходимо и достаточно, чтобы существовала
дважды непрерывно дифференцируемая
скалярная функция
было потенциальным в областиV,
необходимо и достаточно, чтобы существовала
дважды непрерывно дифференцируемая
скалярная функция
![]() такая, что
такая, что![]() Функцияu(M)
при этом называется потенциалом
поля
Функцияu(M)
при этом называется потенциалом
поля
![]()
При
выполнении условий (27.19) криволинейный
интеграл 2-го рода не зависит от линии
интегрирования, соединяющей точки
![]() иM.
Поэтому для нахождения потенциала
векторного поля
иM.
Поэтому для нахождения потенциала
векторного поля
![]() применяют формулу
применяют формулу
![]()
где
![]() – некоторая фиксированная точка,
– некоторая фиксированная точка,
![]() –произвольная
точка,
–произвольная
точка,
C – произвольная постоянная.
Векторное
поле
![]() называется гармоническим,
если выполняются следующие условия:
называется гармоническим,
если выполняются следующие условия:
![]()
Потенциал u(M) гармонического поля является решением уравнения Лапласа
![]() (27.20)
(27.20)
Функция
![]() удовлетворяющая уравнению Лапласа
(27.20), называетсягармонической.
удовлетворяющая уравнению Лапласа
(27.20), называетсягармонической.
Пример
1. Найти поток
векторного поля
![]() через верхнюю сторону части поверхности
через верхнюю сторону части поверхности![]() отсеченной плоскостью
отсеченной плоскостью![]()
Решение. Нахождение потока векторного поля сводится к вычислению поверхностного интеграла 2-го рода по формуле (27.13):
![]()
Спроектировав
поверхность параболоида
![]() на плоскостьxOy,
сведем вычисление поверхностного
интеграла к нахождению двойного интеграла
по области
на плоскостьxOy,
сведем вычисление поверхностного
интеграла к нахождению двойного интеграла
по области
![]() представляющей собой круг
представляющей собой круг![]() Применив формулу (27.9), получим:
Применив формулу (27.9), получим:
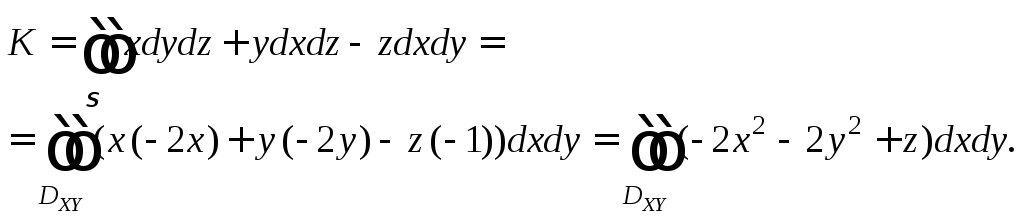
После
подстановки в подынтегральное выражение
![]() имеем интеграл
имеем интеграл![]() который вычислим, перейдя к полярным
координатам
который вычислим, перейдя к полярным
координатам![]()
![]() и с учетом того, что в повторном интеграле
и с учетом того, что в повторном интеграле![]()
![]()

Пример
2. Вычислить
дивергенцию векторного поля
![]() в точке
в точке![]()
Решение.
По условию
![]()
![]()
![]() Согласно формуле (27.14), имеем:
Согласно формуле (27.14), имеем:
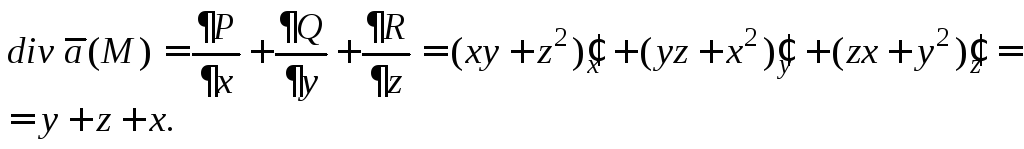
В
точке
![]() имеем:
имеем:
![]()
Так
как
![]() то точка
то точка![]() является стоком поля.
является стоком поля.
Пример
3. Вычислить
циркуляцию векторного поля
![]() вдоль замкнутого контураL:
вдоль замкнутого контураL:
![]()
![]()
![]() если
если![]()
Решение. Циркуляция векторного поля находится с помощью криволинейного интеграла 2-го рода по формуле (27.15), причем вычисление криволинейного интеграла 2-го рода производится с помощью соотношения (26.9), так как мы имеем дело с параметрическим заданием пространственной кривой. В нашем случае получим:
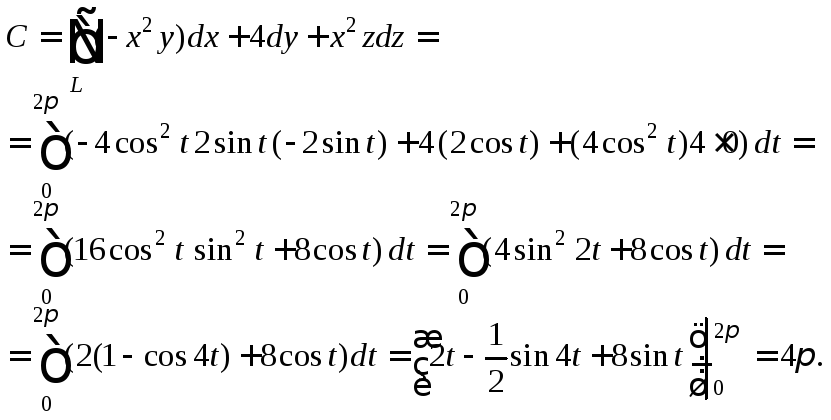
Пример
4. Найти ротор
векторного поля
![]() в точке
в точке
![]()
Решение.
По условию
![]()
![]()
![]() Согласно формуле (27.17), имеем:
Согласно формуле (27.17), имеем:

В
точке
![]() имеем:
имеем:
![]()
Пример
5. С помощью
формулы Стокса вычислить циркуляцию
векторного поля
![]() по контуру треугольника, полученного
в результате пересечения плоскости
по контуру треугольника, полученного
в результате пересечения плоскости![]() с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора![]() этой плоскости.
этой плоскости.
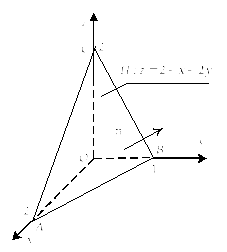
Решение. В результате пересечения плоскости с координатными плоскостями получим треугольник ABC. Укажем на нем положительное
|
Рис. 27.9 |
направление обхода контура ABC согласно условию задачи (рис. 27.9).
Так
как данный треугольник ABC
лежит в плоскости П,
то в качестве поверхности
Найдем
ротор векторного поля
|
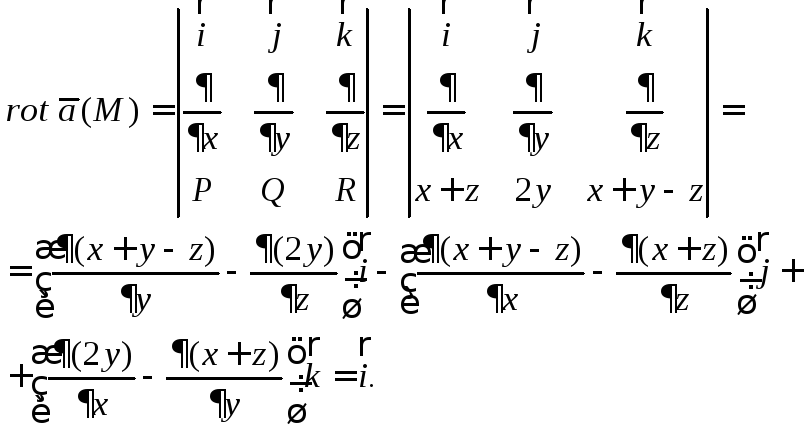
Согласно формуле Стокса (27.18),
![]()
Из
уравнения плоскости П
находим
![]() Поскольку поверхность
Поскольку поверхность![]() задана уравнением в явном виде, а
нормальный вектор
задана уравнением в явном виде, а
нормальный вектор![]() образует с осьюOz
острый угол
образует с осьюOz
острый угол
![]() то для вычисления последнего интеграла
используем формулу (27.9) со знаком «–».
Тогда
то для вычисления последнего интеграла
используем формулу (27.9) со знаком «–».
Тогда
![]()
где
![]() – площадь треугольникаAOB.
– площадь треугольникаAOB.
Задания