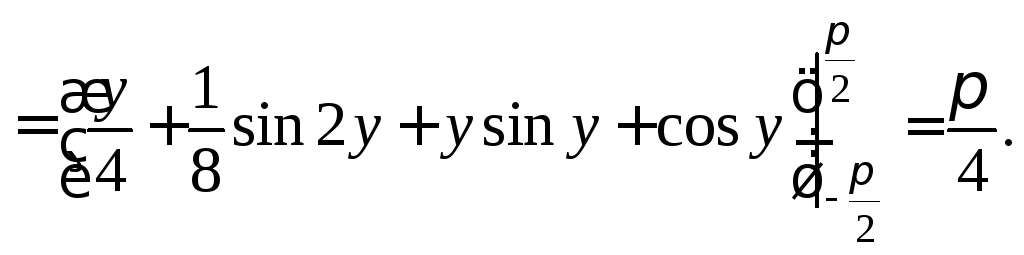24. Двойные интегралы

24.1. Понятие двойного интеграла, его свойства

и вычисление в декартовой системе координат

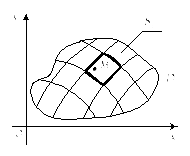
Пусть в замкнутой ограниченной области D плоскости xOy определена непрерывная функция Разобьем указанную область произвольным образом на элементарные плоские области(рис. 24.1), площади которых будем считать соответственно равными Внутри каждой элементарной области выберем произвольную точку

Рис. 24.1

Диаметром области назовем наибольшее из расстояний между любыми двумя точками границы области. Обозначим через диаметры элементарных областей а через– максимальный диаметр, т. е.Составим интегральную сумму функции

f(x; y) в области D:

Устремим так, чтобыЕсли существует предел интегральной суммы, который не зависит ни от способа разбиения областиD на элементарные области, ни от выбора точек внутри каждой из этих областей, то этот предел называетсядвойным интегралом от функции f(x; y) по области D:

При этом говорят, что функция f(x; y) интегрируема в области D, x и y называют переменными интегрирования.

Достаточное условие интегрируемости функции: если определенная в некоторой ограниченной замкнутой области функция непрерывна, то она интегрируема в этой области.

Если функции f(x; y), иинтегрируемы в областиD, то имеют место следующие свойства:

1) линейность:

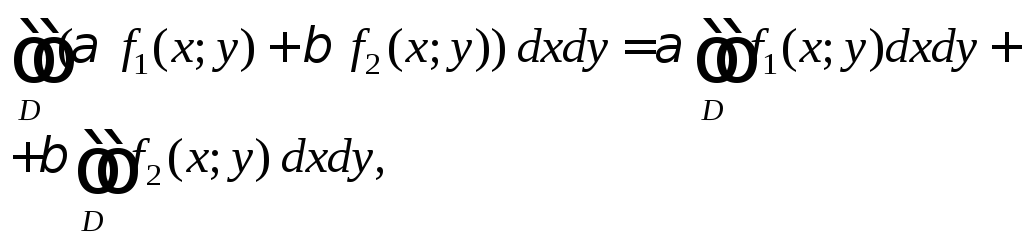
где

2) аддитивность:

причем области ине имеют общих внутренних точек;

3) если выполняется неравенство то

4) оценка модуля интеграла:

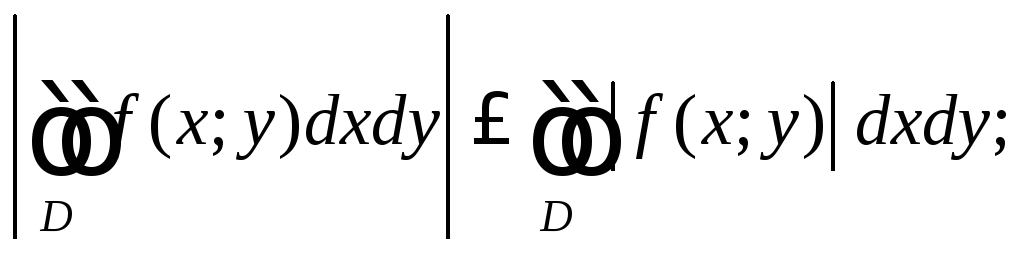
5) если то

где S – площадь области D.

Геометрический смысл двойного интеграла:

(24.1)

где S – площадь области D.

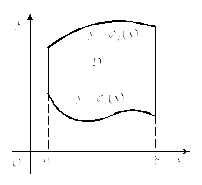
В основе вычисления двойного интеграла в декартовых координатах лежит понятие правильной области. Область D называют правильной в направлении оси Oy, если всякая прямая, проходящая через внутреннюю точку области параллельно оси Oy, пересекает только один раз (только одну) «линию входа» и только один раз (только одну) «линию выхода», которые ограничивают эту область. В частности, это выполняется, если область D имеет вид, приведенный на рис. 24.2.

Рис. 24.2

Рис. 24.3

В случае элементарной области D в направлении оси Oy верна формула

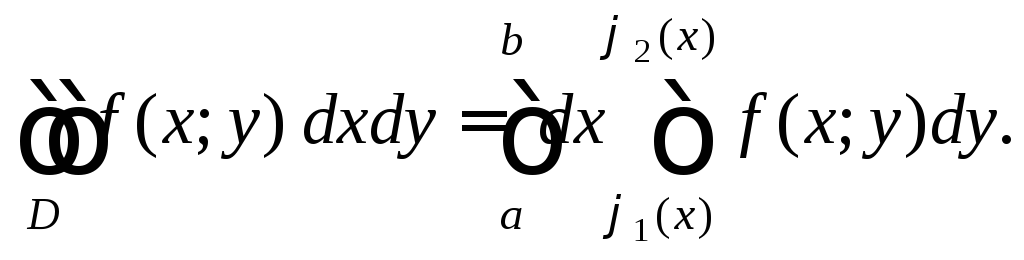(24.2)

Интеграл в правой части равенства (24.2) называется повторным интегралом от функции f(x; y) по области D с внешним интегрированием по x, а –внутренним интегралом по переменной y.

Область D называют правильной в направлении оси Ox, если всякая прямая, проходящая через внутреннюю точку области параллельно оси Ox, пересекает только один раз (только одну) «линию входа» и только один раз (только одну) «линию выхода», которые ограничивают эту область. В частности, это выполняется, если область D имеет вид, приведенный на рис. 24.3.

Тогда

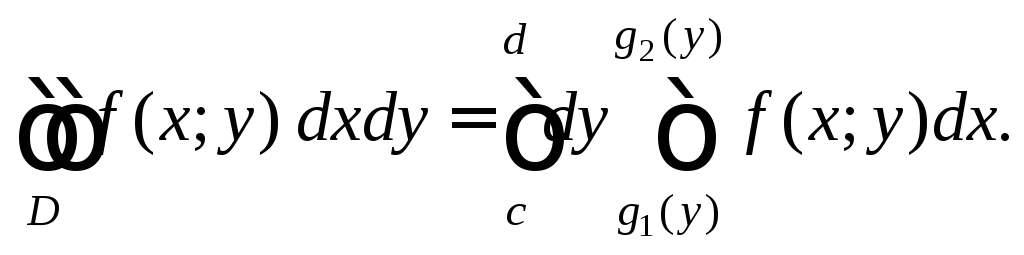(24.3)

Интеграл в правой части равенства (24.3) называется повторным интегралом от функции f(x; y) по области D с внешним интегрированием по y, а 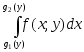–внутренним интегралом по переменной x.

Если область D является элементарной и в направлении оси Ox, и в направлении оси Oy, то для вычисления двойного интеграла можно использовать любую из формул (24.2) и (24.3).

Если область интегрирования D не является элементарной ни в направлении оси Ox, ни в направлении оси Oy, то необходимо произвести разбиение этой области D на конечное количество областей и воспользоваться свойством аддитивности двойных интегралов.

Пример 1. Изменить порядок интегрирования в двойном интеграле:

1) 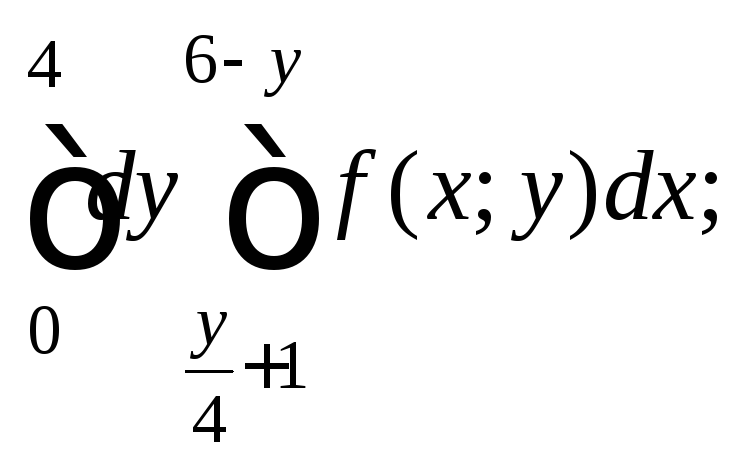2)

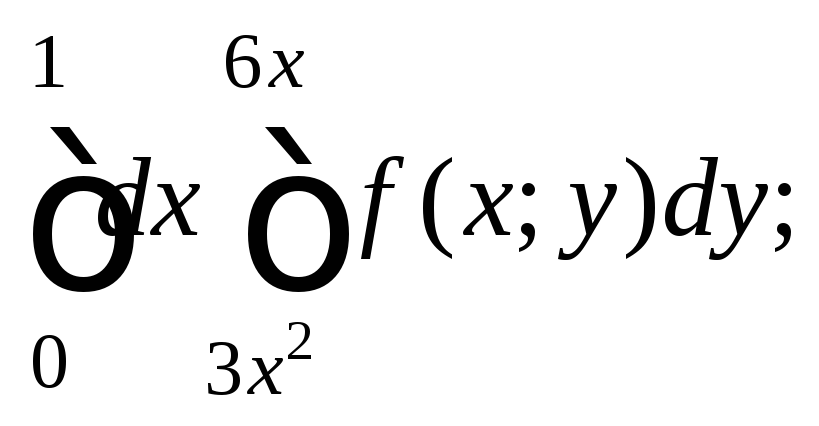3) 4)

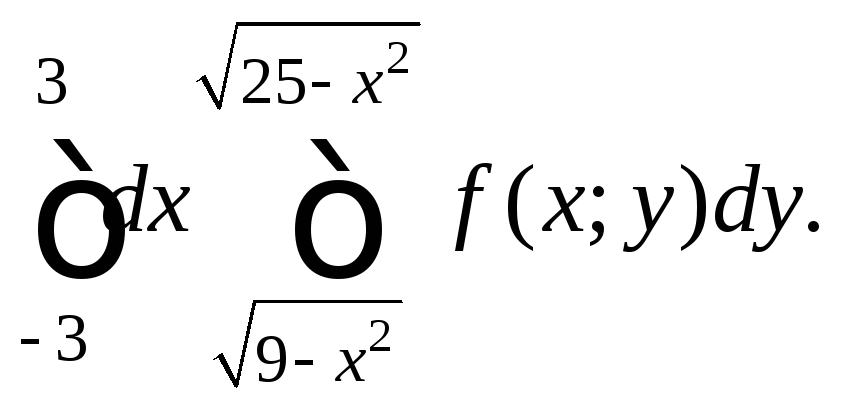
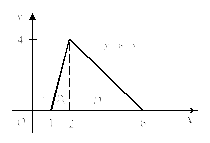
Решение. 1) Область интегрирования ограничена прямыми Изобразим ее (рис. 24.4).

Рис. 24.4

Область интегрирования является правильной в направлении оси Ox, но не в направлении оси Oy. Поэтому для перехода к повторному интегралу с внешним интегрированием по x сначала выразим через эту переменную x уравнения прямых, ограничивающих область D. В результате получим: и

Затем разобьем область на две подобласти и Для каждой из них определим границы изменения переменных x и y:

После применения формул (24.2) и (24.3) получим искомый результат:

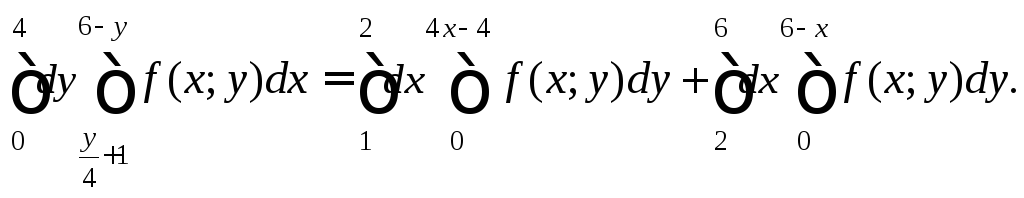
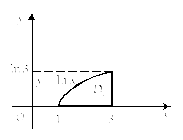
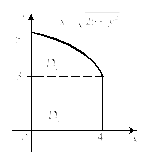
2) Линиями, ограничивающими область интегрирования D, являются координатные оси Ox и Oy, прямая и часть окружности лежащая в первой четверти. Изобразим эту область (рис. 24.5).

Рис. 24.5

Она является правильной в направлении оси Oy, но не в направлении оси Ox. Выразив через переменную y часть окружности, лежащую в первой координатной четверти, получим: Для того чтобы перейти к повторному интегралу с внешним интегрированием по y, разобьем область D на две подобласти и Определив для каждой из них границы изменения переменных x, y и применив формулы (24.2) и (24.3), получим:

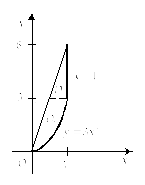
3) Изобразим область интегрирования D с учетом границ изменения переменных x и y. В нашем случае: (рис. 24.6).

Рис. 24.6

Выразим y через x в уравнениях линий, ограничивающих область интегрирования. У нас парабола и прямая Область не является правильной в направлении оси Ox. Поэтому ее необходимо разбить на две подобласти ии для каждой из них определить границы изменения переменныхx и y. С учетом вышесказанного мы имеем следующее:

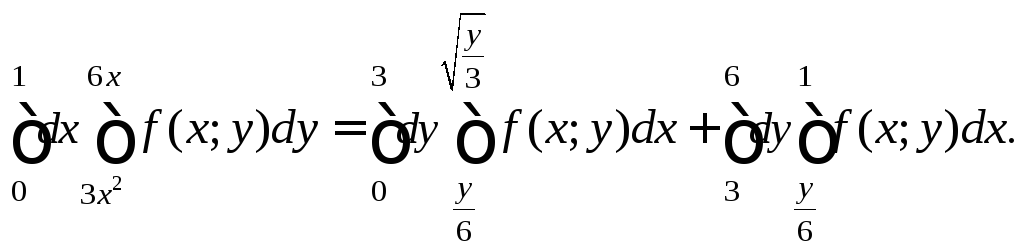
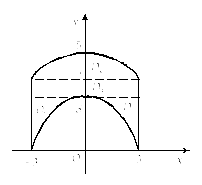
4) Изобразим область интегрирования D, ограниченную прямыми и верхними полуокружностями(рис. 24.7):

Рис. 24.7

Выразим x через y в уравнениях линий, ограничивающих область интегрирования. Одну из окружностей можно представить как объединение двух полуокружностейприиприАналогично, другая окружностьпредставляет собой объединение двух полуокружностей:

при ипри

Отметим, что область D не является правильной в направлении оси Ox. Поэтому чтобы перейти к повторному интегралу с внешним интегрированием по y, необходимо область интегрирования D разбить на четыре подобласти Для каждой из них определим границы изменения переменныхx и y:

Итак, искомый результат выглядит как сумма повторных интегралов по каждой из указанных областей интегрирования:

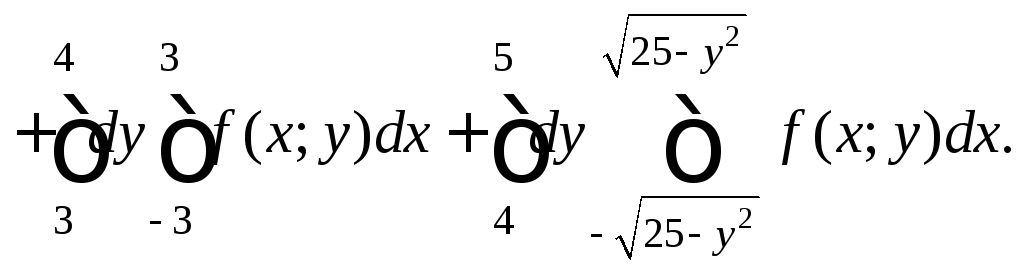
Пример 2. Вычислить двойной интеграл по указанному прямоугольнику:

1)

2)

3)

Решение. 1) Поскольку область – это прямоугольник, то она является правильной областью и в направленииOy, и в направлении Ox. Рассмотрим оба случая и покажем, что результат вычислений интеграла не зависит от порядка интегрирования.

1-й способ. При вычислении двойного интеграла перейдем к повторному интегралу, воспользовавшись формулой (24.2). Вычисляя внутренний интеграл по переменной y и понимая под x постоянную величину, получим:

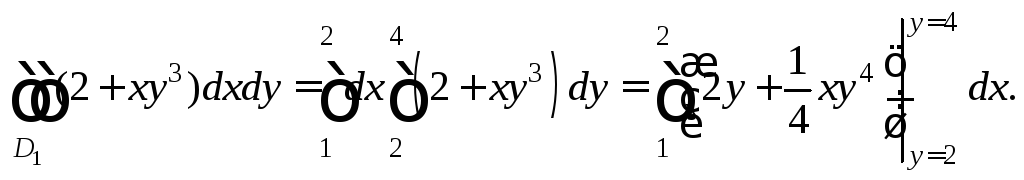
По аналогии с формулой Ньютона–Лейбница подставим вместо y вначале верхний предел интегрирования, а затем – нижний, и составим разность полученных выражений. В результате будем иметь дело с определенным интегралом по переменной x. Исходный интеграл будет равен следующему выражению:

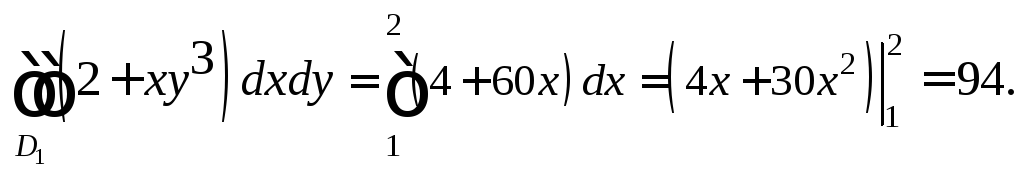
2-й способ. Изменив порядок интегрирования и применив формулу (24.3), получим:

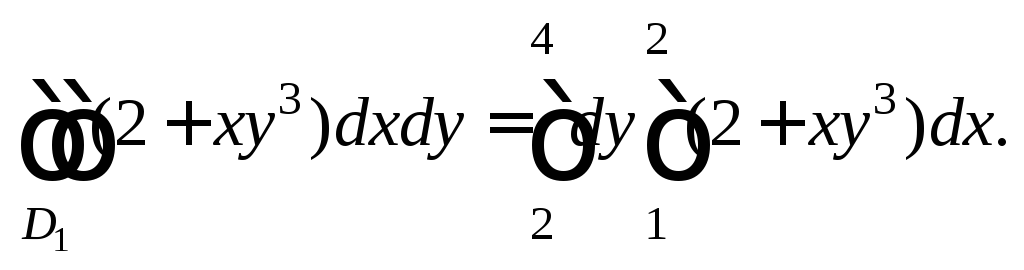
Вычислим внутренний интеграл по переменной x, считая y постоянной величиной, и применим формулу Ньютона–Лейбница. В результате придем к определенному интегралу по переменной y:

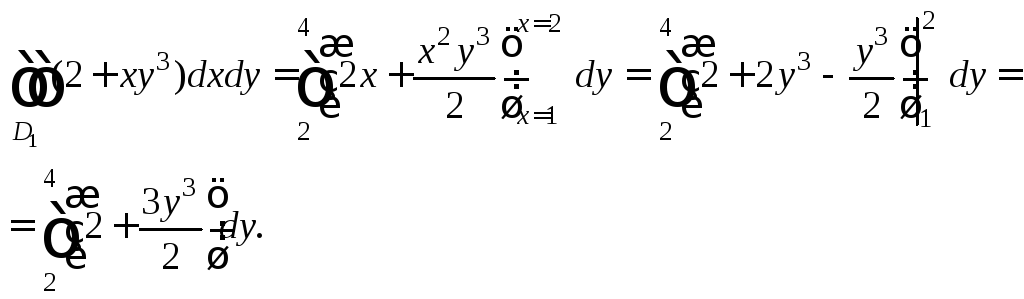
Найдем определенный интеграл:

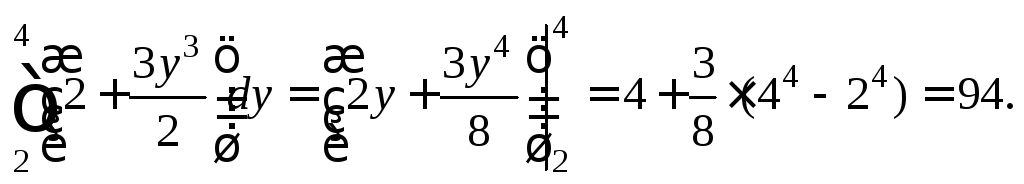
2) Так как и в направленииOy, и в направлении Ox является правильной областью, применим формулу (24.2). Вначале вычислим внутренний интеграл по переменной y, считая x постоянной величиной:

Вычислим полученный определенный интеграл по переменной x с помощью формулы Ньютона–Лейбница:

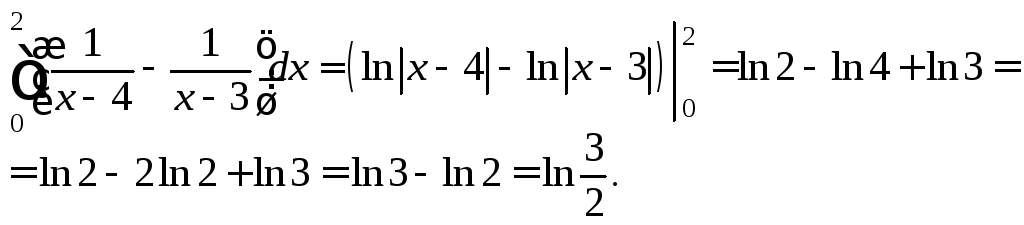
3) Так как прямоугольник – правильная область и в направленииOy, и в направлении Ox, при вычислении двойного интеграла применима как формула (24.2), так и формула (24.3). На основании свойства линейности получим:

Для вычисления первого интеграла более рационально считать область правильной в направлении осиOx и применить формулу (24.3). В случае второго интеграла будем рассматривать область как правильную в направлении осиOy, и применим формулу (24.2). Получим:

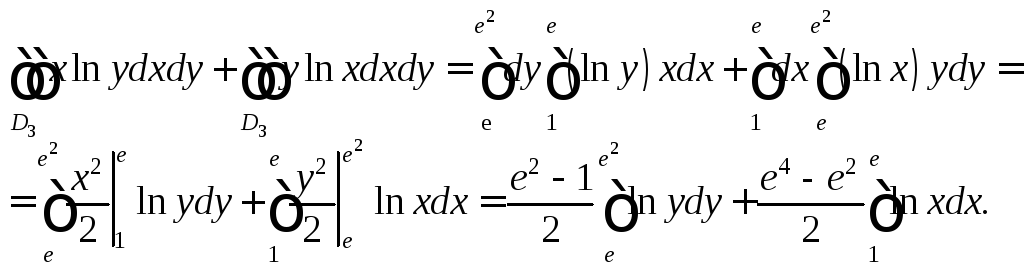
Для вычисления полученных определенных интегралов используем метод интегрирования по частям. Абстрагируясь от буквенного обозначения и вычислив сначала неопределенный интеграл получим следующее:

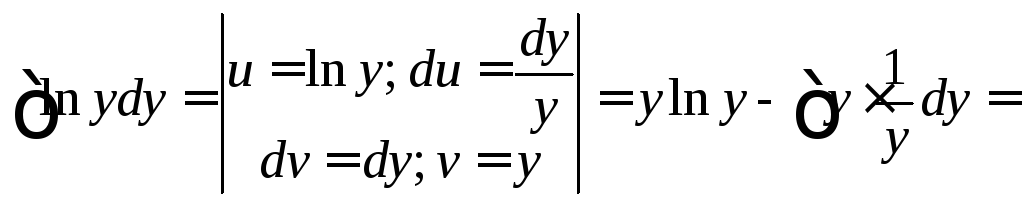
С учетом найденной первообразной после подстановки соответствующих пределов интегрирования получим:

Пример 3. Вычислить интеграл по области, ограниченной указанными линиями:

1)

2)

3)

4)

Решение. 1) Изобразим область интегрирования (рис. 24.8).

Рис. 24.8

Рассматриваемая область является правильной в направлении оси Oy. Поэтому для перехода к повторному интегралу рационально применить формулу (24.2). Предварительно расставим пределы интегрирования, используя изображение области: Перейдя к повторному интегралу с внешним интегрированием по x и вычислив его, получим:

2) Изобразим область интегрирования и убедимся, что она является правильной в направлении оси Ox (рис. 24.9).

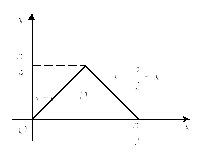
Рис. 24.9

Расставим пределы интегрирования, исходя из изображения области: Вычислим двойной интеграл, перейдя к повторному интегралу по формуле (24.3):

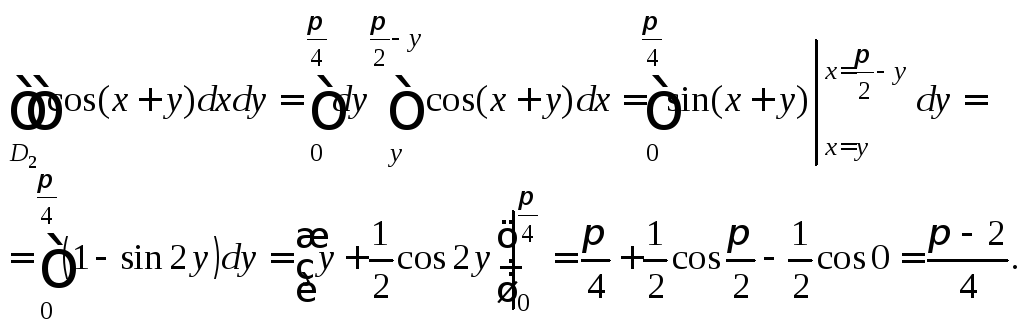
3) Изобразим область интегрирования (рис. 24.10). Она является правильной в направлении обеих осей, но будем считать ее правильной в направлении осиOx. С учетом этого расставим пределы интегрирования:

Вычислим двойной интеграл, перейдя к повторному интегралу по формуле (24.3):

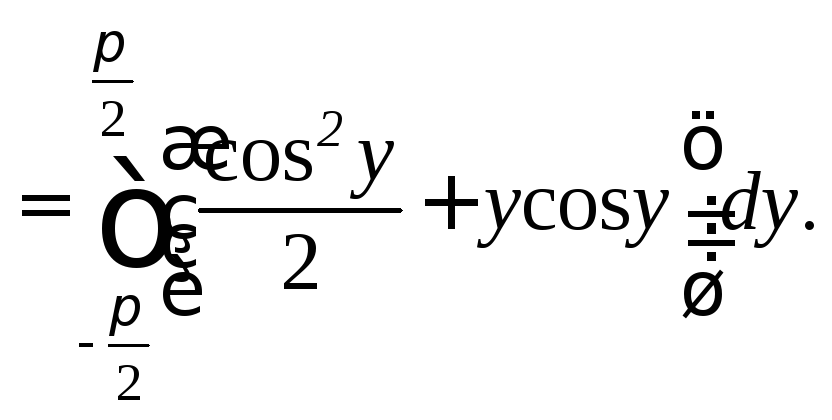
Рис. 24.10

Мы получили определенный интеграл по переменной y. Для вычисления интеграла от первого слагаемого применим формулу понижения степени второго слагаемого – формулу интегрирования по частям. Имеем:

4) Изобразим область интегрирования (рис. 24.11).

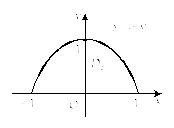
Рис. 24.11

Она является правильной в направлении оси Oy. Учитывая это, расставим пределы интегрирования:

Вычислим двойной интеграл, перейдя к повторному интегралу по формуле (24.2):

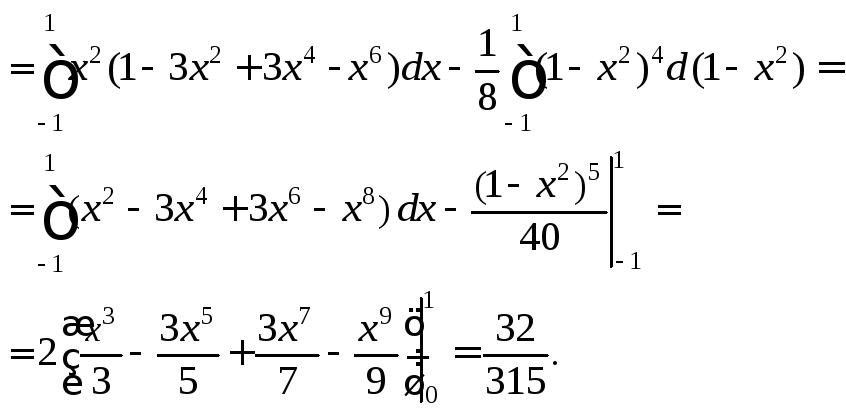
Задания