I уровень

1.1. Найдите нули функцииf(z) и определите их кратности:

1) 2)

3)

1.2. Найдите особые точки функции f(z) и определите характер каждой особой точки (в случае полюса определите его порядок):

1) 2) 3)

4) 5)

II уровень

2.1.Найдите нули функцииf(z) и определите их кратности:

1) 2)3)

4) 5)6)

2.2. Найдите особые точки функции f(z) и определите характер каждой особой точки (в случае полюса определите его порядок):

1) 2)3)

4) 5)6)

III уровень

3.1.При условии, что функцииf(z) иg(z) имеют в точкеполюсы порядкаmи порядкаnсоответственно, определите, является ли точкаособой для функции

1) 2)3)

Если точка aявляется особой точкой, установите ее тип.

3.2.Определите, является ли точкаособой для функцииf(z):

1) 2)

3) 4)

Если да, то каков ее характер?

29.9. Вычеты и их приложения

Вычетом функцииf(z)в особой точкеaназывается коэффициент при первой отрицательной степени ряда Лорана функцииf(z) в проколотой окрестности точкиa:

(29.41)

Вычет функции f(z) в особой точкеaможет быть найден по формуле:

(29.42)

где – положительно ориентированная окружность такая, что функция f(z) аналитична всюду на круге за исключением точки

Если a – устранимая особая точка функции f(z), то и, значит,где контурположительно ориентированная окружностьтакая, чтоf(z) аналитична всюду на круге

Если a– простой полюс функцииf(z), то

(29.43)

Если функцию f(z) можно записать в виде:

где аналитичны в точкеaит. е.a– простой полюс функцииf(z), то

(29.44)

Если a– полюсk-го порядка функцииf(z), то

(29.45)

Основная теорема о вычетах. Пусть функцияf(z) является аналитической во всех точках односвязной областиD, кроме конечного числа особых точек, и Г – замкнутая положительно ориентированная кривая, которая лежит вDи ограничивает область, содержащую особые точкиТогда

(29.46)

Вычетом функции f(z) в точке (– изолированная особая точка функцииf(z)) называется число, равное противоположному по знаку коэффициенту при первой отрицательной степени ряда Лорана функцииf(z) в окрестности точки

(29.47)

Вычет функции f(z) в точкеможет быть найден по формуле:

(29.48)

где – окружность достаточно большого радиуса, проходимая по часовой стрелке.

В устранимой особой точке вычет может быть и ненулевым (в отличие от конечной устранимой особой точки).

Теорема.Пусть функцияf(z) аналитична на плоскостиĈ, кроме конечного числа точек. Тогда сумма вычетов во всех особых точках, включая и точкуравна нулю.

Пусть функция f(z) аналитична всюду на полуплоскостикроме конечного числа особых точек, которые лежат сверху от действительной оси. Пусть также точкаявляется нулем кратности больше единицы функцииf(z). Тогда справедлива формула

(29.49)

где – особые точки функцииf(z), в которых

Пусть дробно-рациональная функция гдеявляется аналитической на действительной оси. Тогда

(29.50)

где – полюсы функциикоторые лежат в полуплоскости

Если – дробно-рациональная функция отто

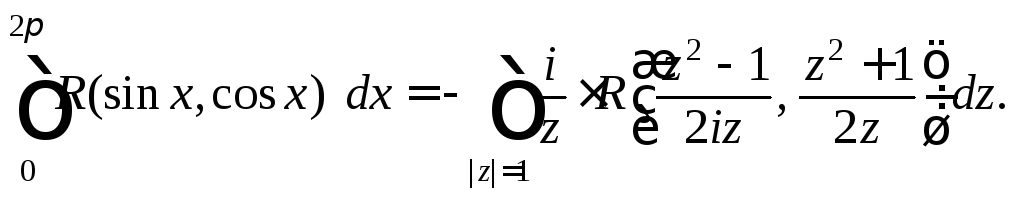
Пример 1. Вычислить вычет функции:

1) 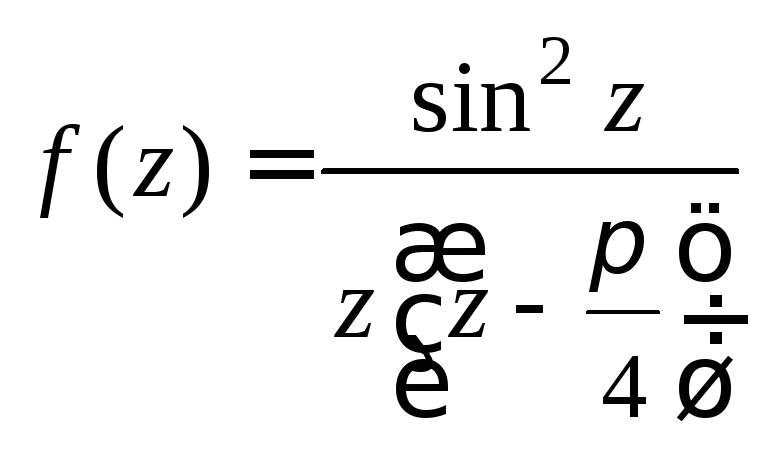в точке2)в точке

Решение. 1) Очевидно, что есть простой полюс функции. Найти вычет в этой точке можно двумя способами: согласно формулам (29.43) и (29.44). Покажем это.

Используя формулу (29.43), получаем:

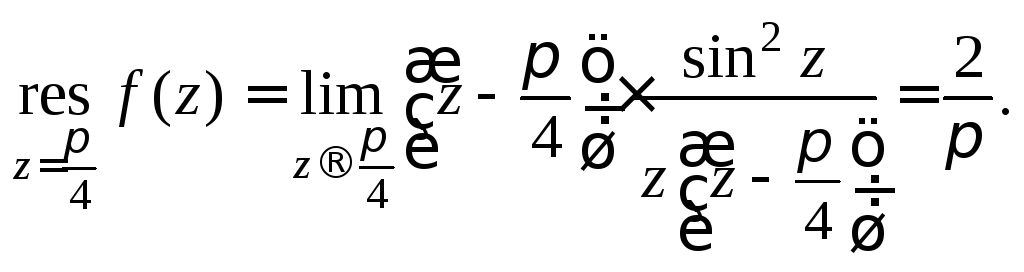
Заданная функция удовлетворяет всем условиям, при которых справедлива формула (29.44). Поэтому,

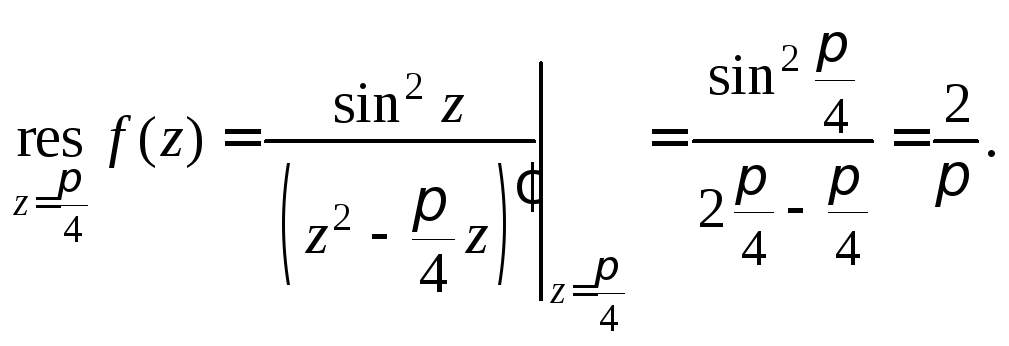
2) Поскольку, в соответствии с формулой Эйлера,

то числитель и знаменатель заданной функции зануляются в точке Для выяснения характера особой точкиразложим числитель в ряд Тейлора по степенямНайдем коэффициенты этого ряда:

Получаем

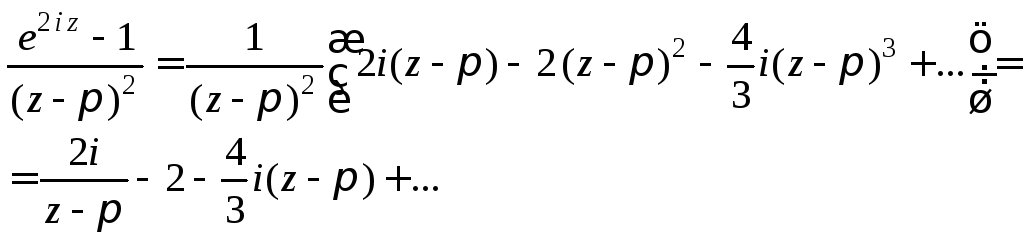
Видим, что – простой полюс данной функции. Однако использовать формулу (29.43) или (29.44) уже не надо. Из полученного разложения имеем:

Пример 2. Вычислить вычет в точке функции:

1) 2)3)

Решение. 1) Поскольку

то есть полюс третьего порядка заданной функции. Тогда согласно формуле (29.45), приимеем:

2) Запишем данную функцию в виде

(29.51)

Выражение (29.51) показывает, что точка есть нуль кратности три знаменателя. Однако в этой точке и числитель равен нулю, причем для негоесть простой нуль (это следует из разложения функциив ряд Маклорена – формула (29.29)). Значит, в отличие от первой функции, рассмотренной в этом примере, точкаесть полюс второго порядка. Для вычисления вычета в ней воспользуемся формулой (29.45) для

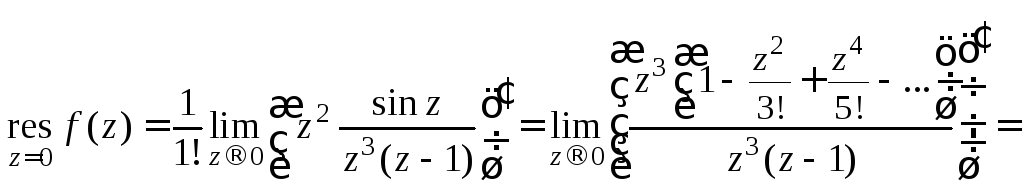
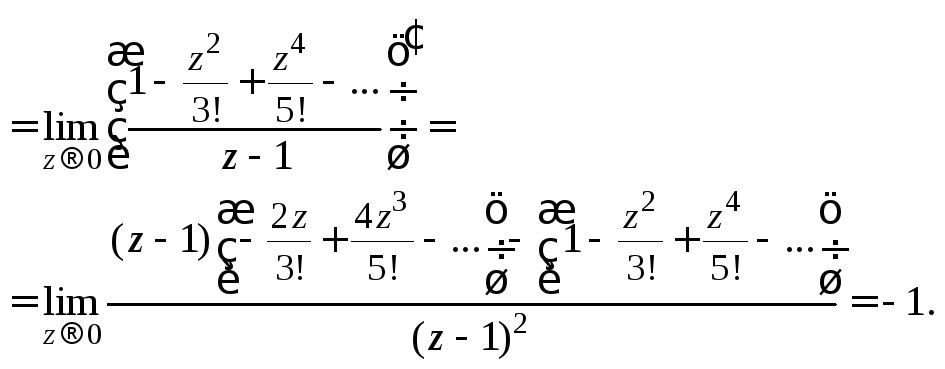
3) Чтобы определить характер особой точки для данной функции, лучше всего использовать разложение экспоненты в ряд Маклорена (29.29), заменив в немz на Тогда

Видим, что коэффициент равенЗначит,причем точкасущественно особая точка.

Пример 3. Вычислить интеграл от функции

по положительно ориентированной окружности:

1) 2)

Решение. Найдем особые точки подынтегральной функции и определим их тип. Нули знаменателя – точки (простой нуль);(двукратные нули);(простые нули). С учетом того, что– нуль кратности два числителя, приходим к заключению, что– простые полюсы;– полюс второго порядка,– устранимая особая точка. Вычислим интеграл от данной функции, основываясь на формуле (29.46).

1) Внутри линии находится только одна особая точка(при).

Используя формулы (29.46) и (29.43), получаем:

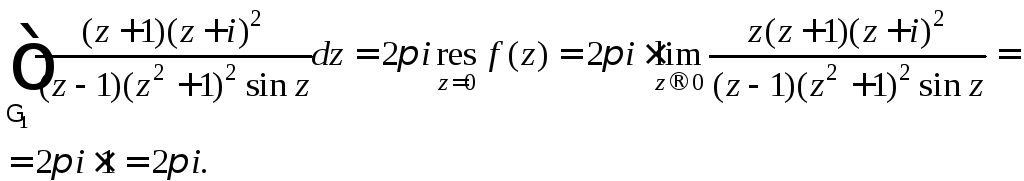
2) Линия имеет внутри четыре особые точки:Поэтому надо вычислить четыре вычета.

Поскольку – простой полюс, то по формуле (29.43) получаем:

Для вычисления вычета в полюсе второго порядка воспользуемся формулой (29.45):

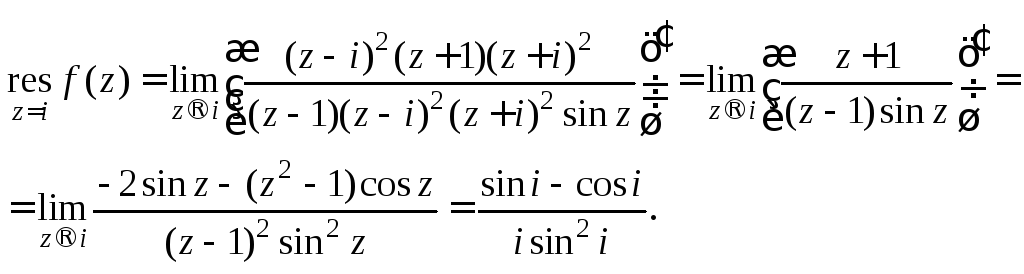
Поскольку – устранимая особая точка, то

Вычет в точке находим, используя формулу (29.43). Получаем

Воспользуемся теперь формулой (29.46) и полученными значениями вычетов:

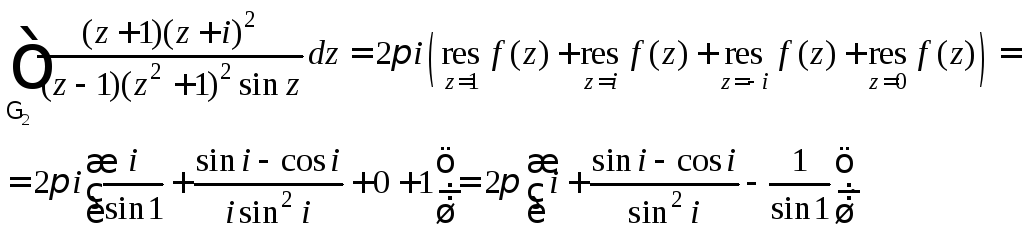
Пример 4. Вычислить

Решение. Преобразуем выражение, которое стоит под знаком вычета:

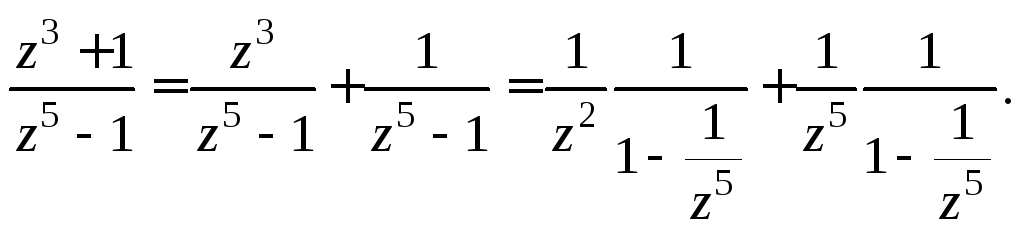
Теперь используем разложение (29.31):

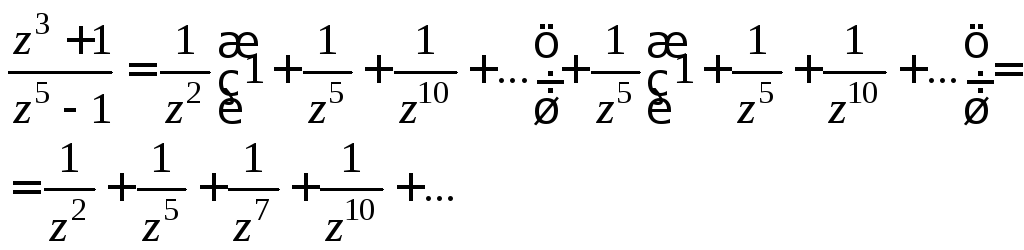
Видим, что т. е.

Пример 5. Вычислить

где Г – окружность

Решение. Внутри окружности лежат шесть полюсов третьего порядка, вне ее – простой полюси точкаОчевидно, что более рационально вычислять сумму вычетов в точкахиСогласно формуле (29.43), получаем:

Для определения вычета в точке найдем несколько слагаемых ряда Лорана. С этой целью сделаем замену переменнойТогда

где через обозначена аналитическая функция в окрестности точкиФункциюможно разложить в степенной ряд:

Возвращаясь к старой переменной, имеем:

Видим, что т. е.Получили следующее значение интеграла:

Пример 6. Вычислить

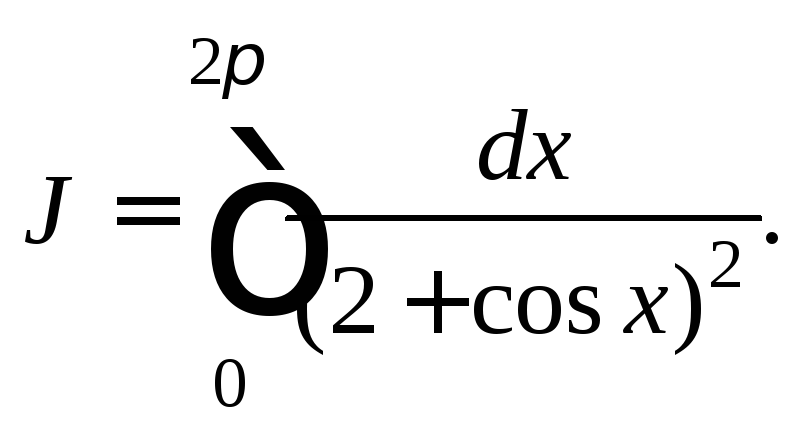
Решение. Сделаем замену переменной Тогда

Приходим к необходимости вычисления интеграла

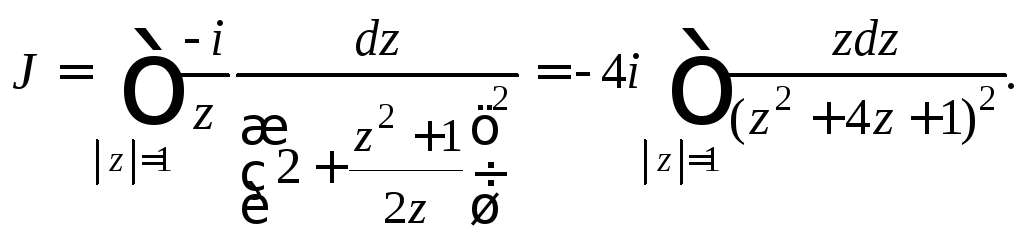
Найдем особые точки подынтегральной функции. Это те значения z, для которых т. е.

Внутри круга лежит только точкаДля подынтегральной функции она является полюсом второго порядка. Значит,

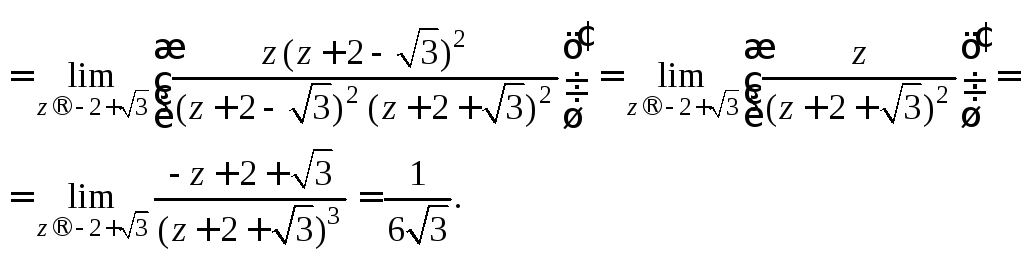
По формуле (29.46) получаем

Пример 7. Вычислить интеграл

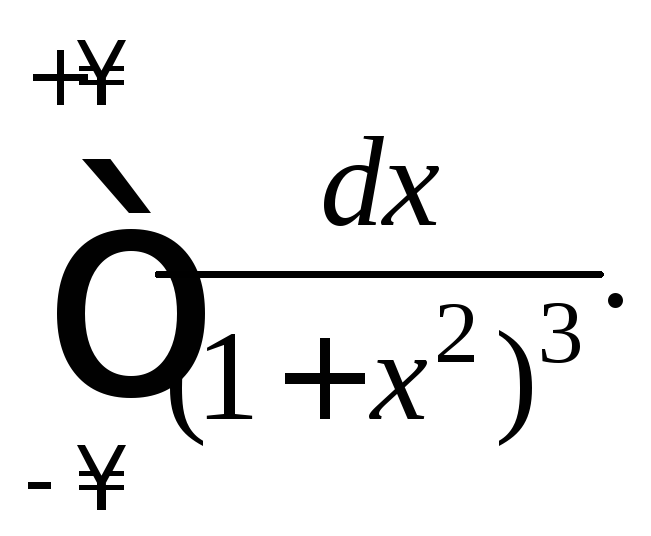
Решение. Функция которая является подынтегральной приудовлетворяет всем условиям, при которых справедлива формула (29.50). Ее особыми точками являются точкиЭто полюсы третьего порядка. В верхней полуплоскости лежит только полюса поэтому

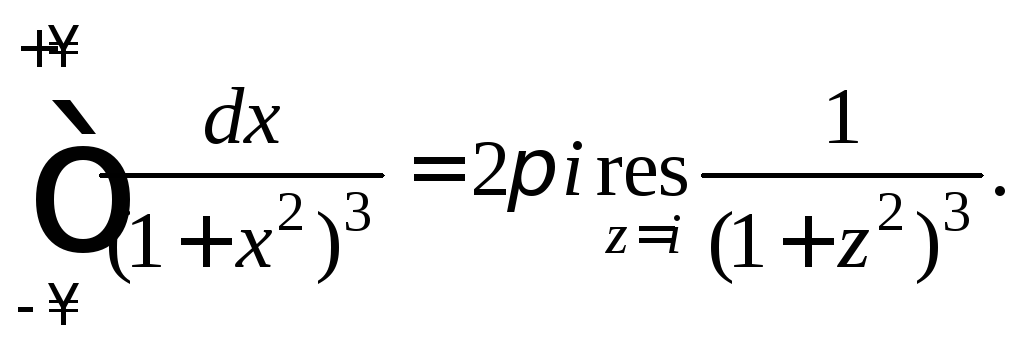
Находим

Получаем

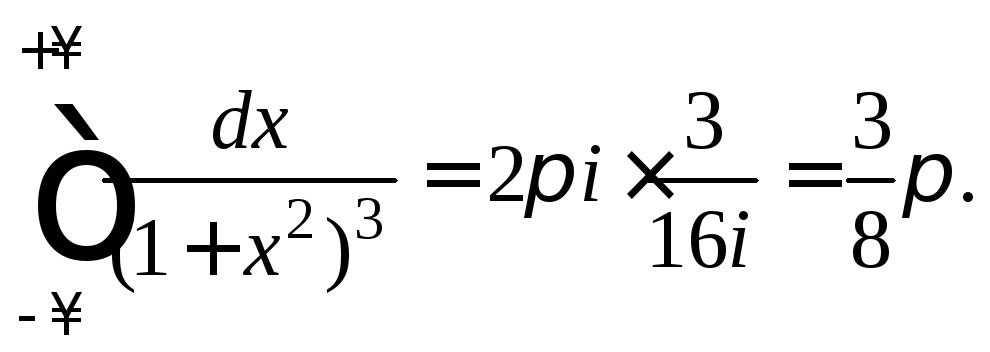
Задания