I уровень

1.1.Выясните, дифференцируема ли функция:

1) 2)

3) 4)

Если функция дифференцируема, то найдите ее производную.

1.2.Найдите коэффициент растяжения и угол поворота при отображениив точке

1) 2)

3) 4)

1.3.Найдите область аналитичности функции, если такая существует:

1) 2) 3)

II уровень

2.1.Найдите производную функцииf(z), еслиf(z) дифференцируема:

2.2.При каком значенииaфункцияf(z) является дифференцируемой:

1) 2)

2.3.Определите действительные функцииитак, чтобы фукнциябыла дифференцируемой.

III уровень

3.1.Восстановите аналитическую функциюf(z) по известной действительнойu(x, y)или мнимойv(x, y) части:

1) 2)

3) 4)

3.2.Зная, что в декартовой системе координат условия Д’Aламбера–Эйлера имеют вид

получите такие условия в полярной системе координат.

3.3.Пусть функцияопределена и аналитична в областиD. Определите, как выражается площадь областиG, являющейся образомD, при отображении

29.4. Однозначные элементарные функции

Определим основные однозначные элементарные функции.

1. Экспонента

Экспонентой комплексной переменной z называется функция, которая определяется равенством:

где

Кроме обозначения для этой функции используют и обозначение

Свойства экспоненты

1.Определена и непрерывна на плоскостиC.

2.Производная существует на всей плоскостиCи выполняется равенство

3.

4.Периодична с основным периодом

2. Тригонометрические функции

Функции косинус и синус комплексной переменнойопределяются равенствами:

(29.7)

Справедлива формула Эйлера

Свойства функций и

1.Определены и непрерывны на всей плоскостиC.

2.Аналитичны наCи выполняются равенства

3.Функцияявляется четной, т. е.а– нечетной, т. е.

4. Периодичны с основным периодом т. е. верны формулы:

З а м е ч а н и е. Может оказаться, что для некоторых значений z  C выполняется

Функции тангенс и котангенс комплексной переменной определяются формулами:

,

Функции тангенс и котангенс являются нечетными и периодическими с основным периодом

3. Гиперболические функции

Гиперболические косинус, синус, тангенс и котангенс комплексной переменной определяются соответственно равенствами:

Свойства гиперболических функций

1. Функции определены и непрерывны на плоскостиC.

2.Производные функцийсуществуют для любогои

3.Справедливы равенства:

(29.8)

4.Функцииthzиcthzопределены и непрерывны всюду на плоскостиC, кроме нулей знаменателей.

Пример 1. Доказать, что для функции справедлива формула

(29.9)

Решение. Пусть Используя свойства степени и формулу Эйлера, получим:

Далее, перемножая выражения в скобках и используя тригонометрические формулы для косинуса и синуса суммы двух аргументов, получаем:

Равенство (29.9) доказано.

Пример 2. Доказать равенство

Решение. Используем определение гиперболического синуса. Тогда

Заданное равенство доказано.

Пример 3. Доказать равенство

(29.10)

Решение. Преобразуем правую часть заданного равенства, используя формулы (29.7):

Выражения перемножаем и по формуле (29.7) получаем:

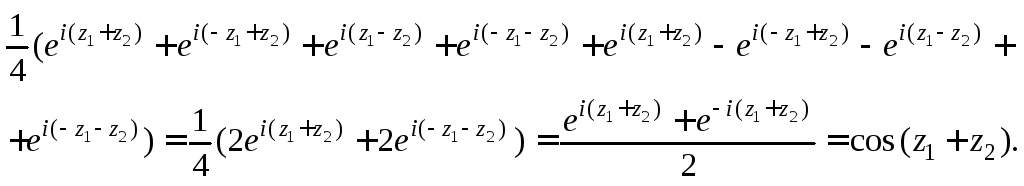
Равенство (29.10) доказано.

Пример 4. Найти действительную и мнимую части функции

Решение. Так как то

Используем далее формулу (29.8). Тогда

Значит, для будет

Пример 5. Выяснить, на какое множество точек плоскости функцияотображает прямую линию с плоскости

Решение. Рассмотрим три случая таких прямых.

1. Пусть z «пробегает» прямую, параллельную мнимой оси Oy: Тогдат. е. образом такой прямой является окружность радиуса с центром в начале системы координатOuv. При этом, когда точка z «пробегает» рассматриваемую прямую один раз (координата t непрерывно меняется от до), то образw «пробежит» (в положительном направлении) соответствующую окружность бесконечное количество раз.

2. Пусть z «пробегает» прямую, параллельную действительной оси Ox: Тогдат. е. множество образов лежит на луче, который выходит из начала системы координат и образует с осью Ou угол При этом, когда точкаz «пробегает» прямую один раз (абсцисса t непрерывно изменяется от до), то образw тоже один раз «пробегает» соответствующий луч (расстояние от начала системы координат до точки w непрерывно растет от 0 до ).

3. Пусть z «пробегает» прямую, которая не параллельна координатным осям. Уравнение такой прямой имеет вид гдеk – угловой коэффициент прямой; b – ордината при Тогда образом такой прямой является кривая

Для точки w, которая лежит на этой кривой (при условии, что ), имеем:Из второго равенства выразивt через и подставив в первое, получимгде

Это уравнение логарифмической спирали.

Пример 6. Выяснить, на какое множество точек функция

отображает полуполосу

Решение. Обозначим данную в условии полуполосу через d. Согласно восьмой формуле (29.8), для функции имеемНайдем сначала образ лучаОчевидно, что он отображается на множество точекПоскольку дляимеемто в плоскостиобразом лучабудет луч Г₁ Аналогично определим, что интервалотображается на множествокоторое является интервалом Г₁: И наконец, лучпреобразуется в множествокоторое является лучом Г₃: Выберем внутреннюю точкуполосыДля этой точки получаем следующие значения:–образ принадлежит четвертой координатной четверти. Это значит, что внутренние точки полосы d отображаются на внутренние точки множества D четвертой четверти, причем это взаимно-однозначное отображение.

Задания