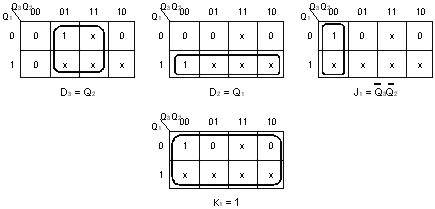1.2 Логические функции

Логическая переменная F называется логической функцией переменных а,в,с и т.д., если каждому набору значений переменных а,в,с и т.д. поставлено в соответствие одно из значений переменной f

F = f (а,в,с...).

Функции считаются различными, если значениеFотличается хотя бы для одного из наборов.

^{Если имеется} nпеременных, тогда число наборов, которые можно построить равно

_Кn=

^{Число функций будет равно} N_n=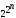

n=1N₁=4

n=2N₂=16

n=3N₃=256

Формы представления логических функции

1. Словесно.

2. Таблица истинности – таблица, содержащая все возможные комбинации всех входных переменных вместе с соответствующими значениями выходных переменных, т.е. значениями функциями.

3. Алгебраическая форма записи.

4. Графический способ записи с помощью карт Карно.

Переход от табличной формы к алгебраической форме записи функции

Чтобы перейти к алгебраической форме в таблице истинности каждому набору в соответствие ставится минтерм и суммируется.

Минтерм – это конъюнкция (логическое произведение), в которое входят все аргументы в прямой или инверсной форме.

Каждый минтерм соответствует одному из значений в таблице истинности. Если переменная в наборе 0, то в минтерм она включается в инверсной форме, если 1, то в прямой.

Пример:

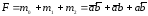
Такая форма представления называется совершенной дизъюнктивной нормальной формой (СДНФ).

1.3 Минимизация логических функций

Минимизацией называют преобразование заданной булевой функции с целью уменьшения общего числа переменных и операций. Процесс минимизации имеет важное значение при технической реализации дискретных устройств, так как при этом уменьшается общее количество элементов, увеличивается надежность и устройства становятся боле экономичными.

Степень минимизации оценивается по числу вхождений, в том числе и повторяющихся, логических переменных в запись логической функции (оценка (цена) по Квайну).

F = = =

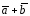Σ_кв=6 Σ_кв=2 Σ_кв=2

Минимизация может быть выполнена различными методами. Алгебраический метод. Алгебраический метод основан на применении законов булевой алгебры к заданной булевой функции. Причем функция может быть задана в произвольной форме.

1.3.1. Минимизация логических функций с помощью карт Карно

Для минимизации функций относительно небольшого числа переменных (k<6)наиболее простым и наглядным является графический метод, использующий карты Карно.При использовании этого метода исходная функция представляется на карте Карно. Минтермы, соответствующие двум соседним (в столбце или ряду) клеткам карты Карно, отличаются значениями только одной переменной. Поэтому дизъюнкция этих минтермов дает одну импликанту, в которой исключена переменная, имеющая взаимоинверсные значения.

Пример карт Карно для числа переменных 2 и 3:

n=2n=3

Чтобы выделить на карте Карно клетки, представляющие одну импликанту, их графически объединяют (обводят тонкой линией). Импликанта представляется на картах Карно двумя, четырьмя, восьмью объеди­ненными клетками. Такое объединение клеток на картах Карно эквивалентно выполнению операции склеивания минтермов и поз­воляет получать более простое выражение логической функции. Поэтому для минимизации логических выражений вместо их алге­браических преобразований можно выполнять соответствующее объединение клеток на картах Карно. Объединенные клетки будут соответствовать импликантам, дизъюнкция которых даст сокра­щенную ДНФ или МДНФ заданной функции. Чем больше клеток входит в объединение, тем меньше переменных входит в соответ­ствующую импликанту, т. е. проще получаемая ДНФ.

Таким образом, минимизацию логических выражений можно выполнять графическим объединением на карте Карно клеток, занятых 1, и последующим получением алгебраического выражения функции в виде сокращенной ДНФ, каждая импликанта которой соответствует объединению нескольких клеток (минтермов) или одной необъединенной клетке. Процесс получения алгебраического выражения функции, представленной на карте Карно, т. е. пере­ход от графического представления к алгебраическому, называется считыванием. При этом каждое объединение клеток считывается в виде импликанты, в которую входят переменные или их инверсии, общие для всех минтермов, соответствующих этим клеткам. Необъединенные клетки считываются в виде соответствующих минтер­мов.

Полученные на основании законов булевой алгебры правила минимизации путем объединения на картах Карно клеток, заня­тых 1, формулируются для функций 4переменных следующим образом.

1. Объединяются две соседние клетки в столбце или ряду, четыре соседние клетки, составляю­щие квадраты.

2. Объединяются клетки или па­ры клеток, крайние в столбцах или рядах.

3. Объединяются полные столбцы или ряды, пары рядом расположенных столбцов или рядов, а также крайние столбцы или ряды на карте.

Карты Карно функций пяти или шести переменных можно представить как две или четыре рядом размещенные карты для четырех переменных. В пределах каждой половины карты Карно пяти переменных и каждой четверти карты шести переменных клетки объединяются по тем же правилам, как и для функции четырех переменных. Объединение клеток, расположенных в разных половинах и четвертях, выполняется соответствии со следующим правилом (оно справедливо и для функций четырех и менее переменных).

4. Объединяются клетки, пары соседних клеток, квадраты, столбцы, ряды, пары соседних столбцов и рядов, расположенные симметрично относительно вертикальной или горизонтальной оси карты Карно.

Количество импликант в получаемой сокращенной ДНФ равно сумме числа объединений и необъединенных клеток. Для получения МДНФ следует включать в каждое объединение максимально возможное число клеток и выбирать такой вариант объединения клеток, чтобы общее число объединений и оставшихся необъедененых клеток было минимально. При этом одна и та же клетка может входить в несколько объединений

Используя различные варианты объединений для некоторых функций, можно получать несколько различных МДНФ, одно из которых выбирается для реализации в цифровом устройстве.

Если для заданной функции имеются безразличные наборы входных переменных, которые обозначаются знаком Хв соответ­ствующих клетках карты Карно, то можно доопределить функцию, чтобы получить более простую МДНФ. В этом случае при минимизации функции с помощью карт Карно в объединения включаются те клетки, отмеченные знакомX,кото­рые дают расширение объединений и уменьшение их количества.

Клетки карты Карно, не занятые 1, со­ответствуют минтермам, входящим в состав СДНФ инверсии заданной функции. Поэтому, объединяя клетки, не занятые 1, сог­ласно приведенным выше правилам можно получить МДНФ для инверсии функции.

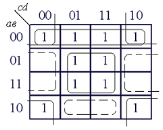
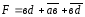
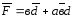
Примеры минимизации с помощью карт Карно: