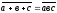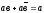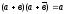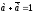Курс лекций по дисциплине: «цифровая электроника »

для студентов специальности,“ Промышленная электроника ”

Минск бгуир 2010 Введение

Интегральная микросхема (интегральная схема - ИС) - микроэлектронное изделие, выполняющее определенную функцию преобразования электрических сигналов, которое представляет собой совокупность электрических соединенных компонентов (транзисторов, диодов, резисторов и др.), изготавливаемых в едином технологическом цикле на общей диэлектрической или полупроводниковой основе (подложке).

Основной функцией интегральных микросхем является обработка (преобразование) информации, заданной в виде электрического сигнала: напряжения или тока. Электрические сигналы могут представлять информацию в непрерывной (аналоговой) или дискретной (цифровой) форме. Микросхемы, выполняющие обработку этой информации, называются аналоговыми или цифровыми соответственно.

Современные интегральные микросхемы являются сложными электронными устройствами, поэтому используются различные уровни их схемотехнического представления. Наиболее детальный уровень представления - электрическая схема в виде соединения отдельных компонентов. Следующий, более общий уровень - структурная схема, представляющая собой соединение отдельных логических элементов и триггеров (для цифровых схем) или аналоговых каскадов (для аналоговых схем). Эти элементы и каскады выполняют элементарные логические или аналоговые операции, с помощью которых можно реализовать любую цифровую, аналого-цифровую или аналоговую функцию. Они имеют относительно простую, электрическую схему, которая обычно содержит не более десяти - двадцати компонентов. Еще более высокий уровень используется для представления сложно-функциональных БИС и СБИС: микропроцессоров, микро-ЭВМ, аналого-цифровых и цифро-аналоговых преобразователей и др. Их структура представляется в виде соединения функциональных узлов и блоков. Такое представление называется функциональной схемой. Структура входящих в ее состав функциональных узлов и блоков может состоять из десятков и сотен простейших логических элементов и аналоговых каскадов.

На стыке микроэлектроники и цифровой техники развивается самостоятельная область науки и техники - цифровая электроника, предметом которой являются принципы и методы схемотехнического проектирования цифровых интегральных микросхем, которое включает разработку их структуры (функционально-логическое проектирование) и электрической схемы (схемное проектирование). Непрерывное повышение степени интеграции проектируемых микросхем, обеспечивающее реализацию на одном кристалле целых цифровых систем, требует от специалиста знания принципов работ базовых логических элементов, триггеров, комбинационных устройств и устройств последовательностного типа.

1. Математический аппарат цифровых систем

1.1 Основы булевой алгебры

1.1.1 Основные положения и законы булевой алгебры

Основным математическим аппаратом, используемым при анализе и синтезе дискретных элементов и устройств, является булева алгебра (алгебра логики, алгебра Буля). В булевой алгебре широко используется понятие “высказывание”. Высказыванием будем называть простое повествовательное положение, о котором можно сказать, что оно ложно или истинно, но не то и другое одновременно. Любое высказывание можно обозначить символом X и считать, что X=1, если высказывание истинно, а X=0, если высказывание ложно. Логическая (булева) переменная – такая переменная X, которая может принимать только два значения: X={0,1}. Из двух простых высказываний X1 и X2 можно образовать более сложные высказывания, используя операции “И”, “ИЛИ”, “НЕ”. Сложные высказывания также принимают значения “истинно” или “ложно”, т.е. 1 или 0. Смысл логических операций над простыми высказываниями X1 и X2 и значениями сложных высказываний можно представить в виде таблиц истинности: “ИЛИ”, “И”, “НЕ” соответственно

Таким образом, простые высказывания являются переменными, а более сложные высказывания – функциями. Причем как переменные, так и функции могут принимать только значения 0 или 1. Булева алгебра может быть определена как алгебра, содержащая 3 операции “И” (конъюнкция), “ИЛИ” (дизъюнкция), “НЕ” (отрицание) над множеством элементов, каждый из которых принимает два значения 0 или 1. Результаты выполнения операций над множеством элементов также принимают два значения 0 или 1.

Таблица 1.1

Определение логических операций