Примеры алгебраического метода доказательства теорем:

15. а+вс = а1 + вс = а(1 + в + с) + вс = а1 + ав + ас + вс = аа + ав + ас +вс = = а(а + в) + с(а + в) = (а + в)(а+с)

20.

Табличный метод доказательства теоремы де-Моргана

а	в	а+в
0 0 1 1	0 1 0 1	0 1 1 1	1 0 0 0	1 1 0 0	1 0 1 0	1 0 0 0

1.1.2 Формы представления функций булевой алгебры

Существует несколько способов задания функций булевой алгебры. Ранее был рассмотрен табличный способ, при котором каждому набору значений переменных в таблице истинности отмечается значение логической функции. Однако при анализе свойств функции такая запись является достаточно громоздкой. Проще выглядит аналитическая запись в виде формул.

Рассмотрим фиксированный набор переменных 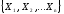на котором задана функция булевой алгебры. Так как любая переменная может принимать значения 0 или 1, то набор переменных может быть представлен двоичным числом, десятичный эквивалентiкоторого определяется отношением:

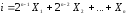
Пусть имеется функци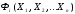я , которая представляет собой набор переменных, связанных через одну из логических операций (ИЛИ, И). Функция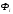называется термом, который имеет две разновидности: дизъюнктивный терм и конъюнктивный терм. Дизъюнктивный терм – набор переменных в прямой или инверсной форме, связанных между собой через операцию “ИЛИ”.

Аналитическое обозначение дизъюнктивного терма выглядит следующим образом:

Конъюнктивный терм – набор переменных в прямой или инверсной форме, связанных между собой через операцию “И”. Конъюнктивный терм обозначается следующим образом:

Ранг терма rопределяется количеством переменных, входящих в данный терм. Например: 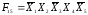,r=5, а для 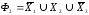,r=3.

Существуют две основные канонические формы аналитического представления функций булевой алгебры: дизъюнктивная и конъюнктивная. Это положение вытекает из следующих теорем.

Теорема 1. Любая таблично заданная функция булевой алгебры может быть представлена в виде дизъюнкции конъюнктивных термов

где i– номер наборов, при которых функция равна 1.

Теорема 2.Любая таблично заданная функция булевой алгебры может быть представлена в виде конъюнкции дизъюнктивных термов

,

где k– количество наборов переменных, для которыхФ=0.

Кроме того следует различать нормальную форму и совершенную нормальную форму представления функции булевой алгебры. Нормальные формы объединяют термы переменного ранга, а совершенные нормальные формы объединяют только термы одного ранга, который равен максимальному количеству переменных, на котором задана функция.

Таким образом, функции булевой алгебры могут существовать в дизъюнктивной нормальной форме (ДНФ) и в совершенной дизъюнктивной нормальной форме (СДНФ), а также в конъюнктивной нормальной форме (КНФ) и конъюнктивной совершенной нормальной форме (СКНФ).

Булевы функции от двух переменных. Полнота и базис булевых функций.

Общее число булевых функций от n переменных определяется соотношением .

Построим все возможные булевы функции от двух переменных. Общее количество функций будет равно 16, их значения представлены в виде таблицы.

Таблица 1.3

Функций двух переменных.

Представленные 16 функций называются элементарными. Функци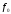и иявляются константами соответственно 0 и 1.

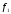- есть конъюнкция (логическое умножение)

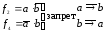
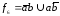альтернатива (сложение по модулю 2)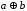

дизъюнкция

функция Вебба (ИЛИ-НЕ)

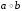
эквивалентность (равнозначность)

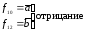
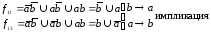
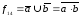функция Шеффера (И-НЕ)

Из булевых функций можно строить новые булевы функции путем подстановки вместо аргументов других функций.

Система булевых функций называется полной в классе 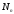, если любая функция в классеявляется суперпозицией этих функций. Под классомподразумеваются все возможные булевы функции от n переменных.

Другими словами полнота – это свойство, позволяющее из элементарных функций выразить любое сложное высказывание.

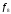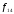С понятием полнота имеет тесную связь понятие базиса. Система является базисом, если теряется полнота при удалении хотя бы одной функции. В качестве базиса можно указать функции и. Например, любая булева функция может быть выражена в базисе И-НЕ (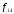):