23.2. Методы нахождения минимума функции одной переменной

Задача нахождения минимума функции одной переменной min/(x) не­редко возникает в практических приложениях. Кроме того, многие методы решения задачи минимизации функции многих переменных сводятся к мно­гократному поиску одномерного минимума. Поэтому разработка новых, бо­лее эффективных одномерных методов оптимизации продолжается и сейчас, несмотря на кажущуюся простоту задачи.

Примечание. В дальнейшем, если не будет особо оговорено, под мини­мумом функции будет подразумеваться локальный минимум.

Нахождение минимума функции осуществляется в два этапа:

1. Приближенное определение местоположения минимума.

2. Вычисление точки минимума x_min c заданной точностью s одним из нижеприведенных методов.

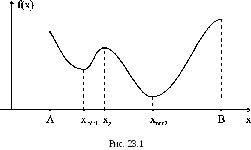
На первом этапе, задав некоторую начальную точку x °, спускаются с заданным шагом h в направлении уменьшения функции и устанавливают ин­тервал длиной 2h, на котором находится минимум, из условия f ( x_m - h ) < f ( x_m ) < f ( x_m + h ). Для функции, изображенной на рис. 23.1, если A < x ° < x _g , будет выделен интервал [a,b] с локальным минимумом x _{min 1}, а если x_g < x ° < B - с глобальным минимумом x _{min 2}, т. е. тот, в области «притяжения» кото­рого оказалась начальная точка x °.

Если на отрезке [a,b] функция f ( x ) унимодальна, т. е. она имеет на этом отрезке единственную точку минимума x _min и слева от этой точки явля­ется строго убывающей, а справа - строго возрастающей, то для вычисления точки минимума с заданной точностью могут использоваться нижеприведен­ные методы:

23.2.1. Метод деления отрезка пополам

Задаются a, b и погрешность s. Вычисляются две точки вблизи середи­ны интервала [a, b]:

1. x₁ = (a + b - s) / 2, x₂ = (a + b + s) / 2.

2. Если f ( x ₁ ) > f ( x ₂ ), то a = x ₁, иначе b = x ₂.

3. Если | b - a | > 2s, тогда повторяем с п.1.

^{4. Вычисляем x}min = ^(a + ^b)/2, JW = ^f(Xmm ^).

Этот метод прост в реализации, позволяет находить минимум разрыв­ной функции, однако требует большого числа вычислений функции для обес­печения заданной точности.

23.2.2. Метод золотого сечения

Золотое сечение - это такое деление отрезка [a, b] на две неравные час­ти при котором отношение большего отрезка ко всему интервалу равно от­ношению меньшего отрезка к большему. При этом имеет место следующее соотношение:

^{(b - x1)/(b - a) = (x1 - a)/(b - x1) = 1- £ = 0.618, £ = (3 - V5)/2 = 0.382.}

О точке, которая расположена на расстоянии £ длины от одного из кон­цов отрезка, говорят, что она осуществляет золотое сечение данного отрезка. Каждый отрезок имеет две такие точки, расположенные симметрично относи­тельно середины. Алгоритм поиска минимума аналогичен вышеописанному методу деления пополам и отличается тем, что вначале точки x₁ и x₂ выби-

У

раются так, чтобы они осуществляли золотое сечение отрезка, и вычисля­ются значения функции в этих точках. В последующем, после сокращения интервала путем отбрасывания небла­гоприятной крайней точки, на остав­шемся отрезке уже имеется точка, делящая его в золотом отношении, ( точка xj на рис. 23.2 ) известно и зна­чение функции в этой точке. Остается лишь выбрать ей симметричную и вычислить значение функции в этой точке для того, чтобы вновь решить, какую из крайних точек отбросить.

f(xi).

Алгоритм метода:

Задаются a, b и погрешность s.

1. Вычисляются две точки

^x1 = а + ^{£(b -} ci\ ^x2 = b ^-£(Ъ ^- ci\ ^yi = ^{f (х}Д ^y2 = ^f(x2^{) .}

2. Если yj > y2, то a = xj, xj = x2, yi = У2, x₂ = b - £ (b-a); У2 = f(x2), иначе b = x2, x2 = xj, y2 = yi, xj = a + £ (b-a),

3. Если | b - a\ > 2s, то повторить п.2.

4. Если yj > y2, то a = xj, иначе b = x2,

^{5. Вычисляется x}_mm = ^(a + ^{b)/2, y}_mm = ^{f (x}_min^).

^yj ⁼

За одно вычисление функции отрезок, на котором находится x_mi_n,

уменьшается в j-£ =0.62 раза, т.е. быстрее, чем метод деления пополам, в ко­тором за два вычисления функции отрезок уменьшается в 0,5 раза.

23.2.3. Метод Фибоначи

На практике количество вычислений значений функции часто бывает ограничено некоторым числом n ( тем самым ограничено и число шагов вы­числений по методу золотого сечения; оно не превышает n-1 ). Метод Фибо­наччи отличается от метода золотого сечения лишь выбором первых двух симметричных точек и формул их пересчета и гарантирует более точное при­ближение к точке x _min за n -1 шаг, чем метод золотого сечения за то же коли­чество шагов. Согласно методу Фибоначи, на нулевом шаге первые две сим­метричные точки вычисляют по формулам xi⁰ = ао + F n ( bo - ao ) / Fn+2 ,

X2⁰ = bo - F n ( bo - ao ) / Fn+2 = ao + F n + 1 ( bo - ao ) / Fn+2 ,

где F _n , F _n + ₁ , F _n + ₂ - числа Фибоначи , определяемые рекурентной формулой

F _k = F _k - 1 + F k - 2 , k=3, 4, ... ; F 1 = F 2 = 1 Запишем первые десять чисел Фибоначи :

F1 =1, F2 =1, F3 =2, F4 = 3, F5 =5, F6 =8, F₇ =13, F8 =21, F₉ =34, F10

=55.

В последующем, после сокращения интервала путем отбрасывания не­благоприятной крайней точки, одна из точек пересчитывается по одной из со­ответствующих формул

_k ^x1^{k = a}k ^{+ F} n - k ^{( b}0 ^{- a}0 ^{) / F}n + 2 ^{, x}2^{k = a}k ^{+ F} n + 1 - k ^{( b}0 ^{- a}0 ^{) / F}n + 2 ^,

Выполняется n - 2 шага, при k = 1, 2, ... , n - 2, после чего отбрасывается крайняя неблагоприятная точка и вычисляется точка минимума x _min = ( a _{n - 1} + b _{n - 1}) / 2. Погрешность вычисления точки минимума не превышает (b₀ - ao) / (2F _{n + 2}), т. е. за три вычисления функции получают точку минимума с по­грешностью не превышающей 1 / 10 первоначального интервала , пять вы­числений - 1 / 26, восемь - 1 / 110.

_Т lim F_n / F_n+2 = (3 -V5)/2, _б

Т.к. ^{n 2} то, при достаточно больших n, вычисле-

П — GO

ния по методу Фибоначи и золотого сечения начинаются практически из од­ной и той же пары симметричных точек.

Алгоритм метода:

Задаются a, b, число вычислений функции n.

1. Вычисляются d = ( b-a ) / F_n+₂ и две точки

^x1 = ^a + ^Fn^{d, x}2 = ^a + ^Fn+1^{d, J}1 = ^{f (x}1 X У2 = ^{f (x}2 ^{) .}

2. Если yi > y2 , то a = xi, xi = x2, У1 = У2, x2 = a + Fn - k d; У2 =f(x2), иначе b = x2, x2 = xi, У2 = У1, xi = a + Fn - k +1 d, yi =f(xi).

п.2 повторяется n-2 раза, при k = 1, 2, ... , n-2.

3. Если У1 > У2 , то a = xi, иначе b = x2

^{4. Вычисляется x}min = ^(a + ^b)/2, JW = ^{f (x}min^{) .}

23.2.4. Метод последовательного перебора

Этот метод не требует предварительного определения местоположения точки минимума. Идея метода состоит в том, что, спускаясь из точки x₀ с за­данным шагом h в направлении уменьшения функции, устанавливают интер­вал длиной 2h, на котором находится минимум, который затем последова­тельно уточняют, повторяя спуск с последней точки, уменьшив шаг и изме­нив его знак, пока не будет достигнута заданная точность. Алгоритм метода приведен ниже.

Задаются x₀, некоторый шаг h и погрешность s .

1. Вычисляем y_o = f (x_o)

2. Определяем направление убывания функции. Если f (x_o+sh) > y_o, то h = -h.

3. Из точки x₀ делается шаг x₁=x₀+h и вычисляются y₁ = f (x₁).

4. Если y₁ < y₀, то x₀ = x₁, y₀ = y₁, и повторить с п.3

5. h = - h / 4. В точке x₁ функция оказалась большей, чем в x₀, следова- тельно, мы перешагнули точку минимума и организуем спуск в обратном на- правлении.

6. Если | h | > s, тогда повторить с п.3

^{7. x}min = ^xo^{, f}min = ^f.

Скорость сходимости данного метода существенно зависит от удачного выбора начального приближения x₀ и шага h. Шаг h следует выбирать как по­ловину оценки расстояния от x₀ до предполагаемого минимума x_mf_n.

23.2.5. Метод квадратичной параболы

Для ускорения спуска к минимуму из некоторой точки x₀ используют локальные свойства функции вблизи этой точки. Так, скорость и направление убывания можно определить по величине и знаку первой производной. Вто­рая производная характеризует направление выпуклости: если f">0, то функ­ция имеет выпуклость вниз, иначе - вверх. Вблизи локального безусловного минимума дважды дифференцируемая функция всегда выпукла вниз. Поэто­му, если вблизи точки минимума функцию аппроксимировать квадратичной параболой, то она будет иметь минимум. Это свойство и используется в ме­тоде квадратичной параболы, суть которого в следующем.

Вблизи точки x0 выбираются три точки xj, x2, x3. Вычисляются значения y₁, y₂, y₃. Через эти точки проводится квадратичная парабола

p( x - x₃) + q( x - x₃) + r = pz + qz + r,

z — x x3, z1 — x1 x3, z2 — x2 x3, r — y 3, (23.1)

_p = ^(y1 ^{- y}3^{) z}2 ^{- (y}2 ^{- y}3^{) z}1 _q = ^(y1 ^{- y}3^{) z}2 ^{- (y}2 ^{- y}3^{) z}1²

^z1^z2^(z1^-z2^{) z}1^z2^(z2^-z1⁾

Если p>0, то парабола имеет минимум в точке z_m = -b/(2a). Следова­тельно, можно аппроксимировать положение минимума функции значением x_m1 = x₃ + z_m и, если точность не достигнута, следующий спуск производить, используя эту новую точку и две предыдущие. Получается последователь­ность x_m1, x_m2, x_m3, ... , сходящаяся к точке x_m.

Алгоритм метода можно записать следующим образом Задается x0, h и s.

1.Выбираем 3 точки: x₁=x_o-h,x₂=x_o-h,x₃=x_o+h, 2. Вычисляем y1 = f (x1), y2 = f (x2), y3 = f (. 3.Проверяем положительность знака второй производной:

h²f'' = y₁ - 2y₂ + y₃ > 0 (см. п. (4.7)), если нет, то начальное приближение

x0 выбрано неудачно (в x0 имеется выпуклость вверх) и следует закончить вы­числения с таким сообщением, если да, то переходим к п.4.

4. Вычисляем z, z₁, z₂, p, q, r, z_m по вышеприведенным формулам

(23.1).

5. Переименовываем точки, отбрасывая точку x₁:

6. Проверяем |z_m | < s, если нет, то повторяем с п.4.

^xm = ^x3 + ^zm^{, y}m = ^{f (x}m X ^конец.

Данный метод сходится очень быстро и является одним из наилучших методов спуска. Следует отметить, однако, что вблизи минимума расчет по приведенным здесь формулам для p и q приводит к накоплению погрешности из-за потери значащих цифр при вычитании близких чисел. Поэтому разные авторы предлагают свои эквивалентные формулы, счет по которым более ус­тойчив. Кроме того, в алгоритм вносятся некоторые поправки, позволяющие предусмотреть различные неприятные ситуации - переполнение, деление на 0, уход от корня.

23.2.6. Метод кубической параболы

Данный метод аналогичен предыдущему, но за счет использования ап­проксимации кубической параболой имеет более высокую сходимость, если функция допускает простое вычисление производной. При его использовании вблизи точки x0 выбираются две точки xi и x2 (обычно x₁ = x₀), вычисляются

значения функции y₁, y₂ и ее производной D₁ = f(x₁), D₂ = f'(x₂). Затем че­рез эти точки проводится кубическая парабола, коэффициенты которой опре­деляются таким образом, чтобы совпадали значения производных параболы и функции:

p(x - x₂) + q( x - x₂) + r (x - x₂) + s = pz + qz + rz + s = P( z),

z=x-x₂,z₁=x₁-x₂,

P(0) = У2, P(0) = D2, P(z1) = У1, P'(z1) = Д.

Как нетрудно убедиться, коэффициенты параболы вычисляются по сле­дующим формулам: s = У2, r = D2,

^p = ^(D1 ^{- D}2 ^{- 2(y}1 ^{- y}2 ^{- D}2 ■ ^z1^)/z1^{)z2, q} = ^(D2 ^{- D}1 + ^3(y1 ^{- y}2 ^{- D}2 ^ ^z1^)/z1^)/z1^.'

Поэтому приближенное положение минимума можно получить по фор­муле x_m1=x₂+z_m и, если точность не достигнута, следующий спуск произво-

Известно, что кубическая парабола имеет минимум в точке дить уже из точек x₂, x_m1 (точка x_j отбрасывается). Если подкоренное выра­жение окажется отрицательным, то спуск следует производить до точки пере­гиба параболы z_m1 = -q /3p . Следует также убедиться, что в начальной точке

a, D₂ - D _ функция вогнута вниз — -- > o.

Алгоритм метода можно записать следующим образом. Задаются начальное значение x₀, некоторый малый шаг h и s.

1. Вычисляем x₁ = x_o, D₁ = f'(x₁).

2. Если D₁ > o, то изменяем знак h (h=-h).

3. Вычисляем x₂ = x₁ + h, D₂ = f'(x₂).

4. Если (D₂ - D₁)/ h < o, функция вогнута вверх, тогда x₀ выбрана не­удачно и следует закончить вычисления с этим сообщением.

5. Вычисляем y = f (x1), y2 = f (.

6. Вычисляем zj, p, q, r, z_m по вышеприведенным формулам.

^{7. x}1 = ^x2^{, y}1 = ^y2^ ^D1 = ^D2^{, x}2 = ^x2 + ^zm^{, y}2 = ^{f (X}2^{), D}2 = ^f '^(x).

8. Проверяем |z_m| < s, если нет, тогда повторяем п.6.

^{9. x}m = ^x2 + ^Zm^{, y}m = ^{f (x}m ^ ^конец.

Следует отметить, что вблизи точки минимума расчет по приведенным здесь простейшим формулам для p, q не всегда устойчив из-за ошибок округ­ления, поэтому различные авторы рекомендуют использовать несколько пре­образованные формулы.

ЛЕКЦИЯ 24. РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ