КР1

Проанализируем зависимости между представленными переменными на основе корреляционной матрицы (рис.1)

Рис.1 построение корреляционно матрицы

Полученные результаты представлены на рсунке 2.

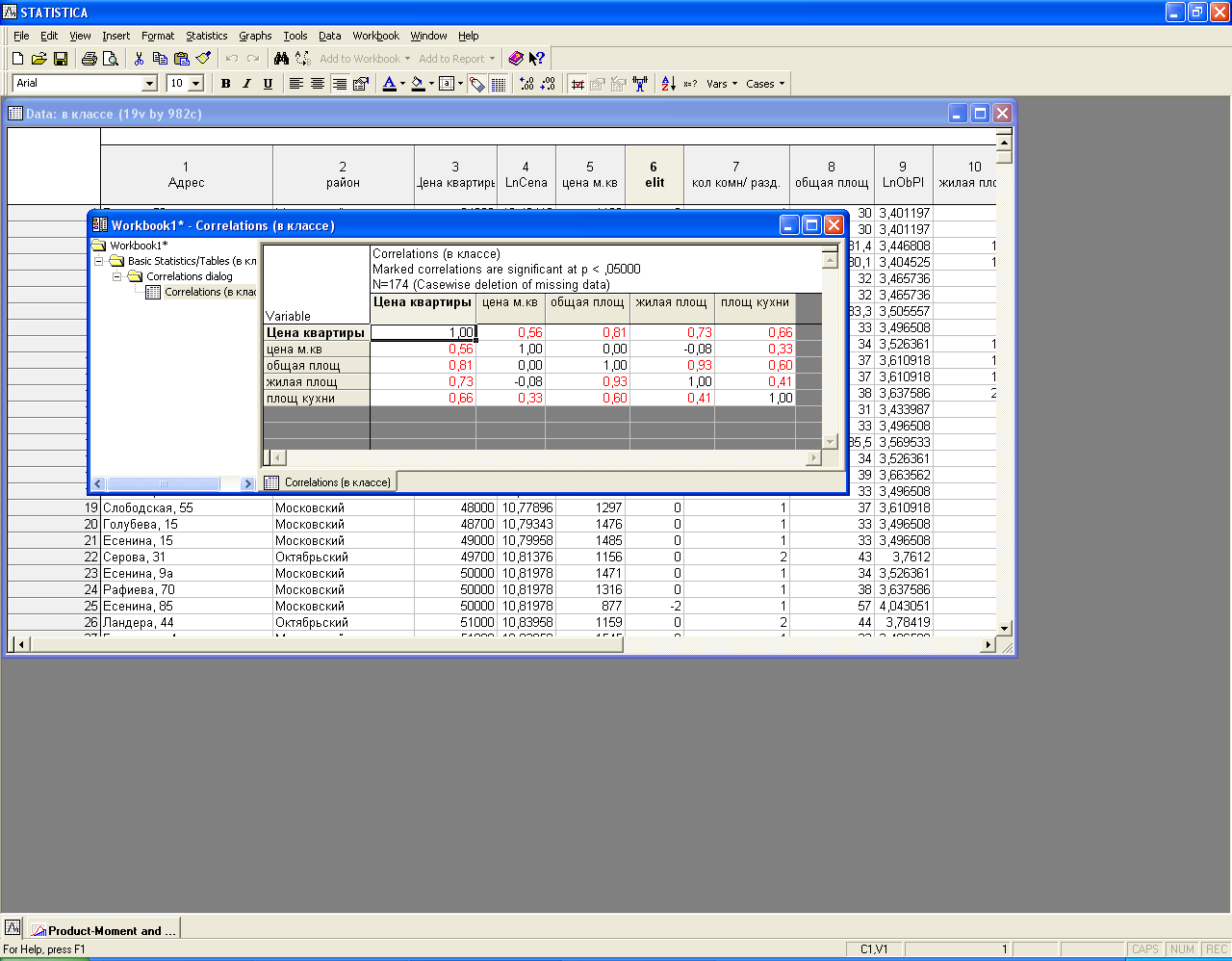
Рис.2 Корреляционная матрица

Как видно, существует достоверная статистическая связь между величиной «Цена квартиры» и остальными (результаты представлены в первой строке). Однако наблюдается тесная связь между «Площадь кухни» и остальными величинами, что в дальнейшем может быть причиной ухудшения качества модели за счет присутствия мльтиколлинеарности.

Построим корреляционное поле между фактором «Цена квартиры» и факторами, характеризующими площади (рис. 2).

Рис.2 Коррелияцонное поле

Как видно из рис.2 с ростом площадей разброс цены квартиры увеличивается. ****** Рассчитаем логарифмы указанных факторов и повторим построение графиков. Как видно на рис. 3 такая форма зависимости будет более предпочтительной и обоснованной с экономической точки зрения.

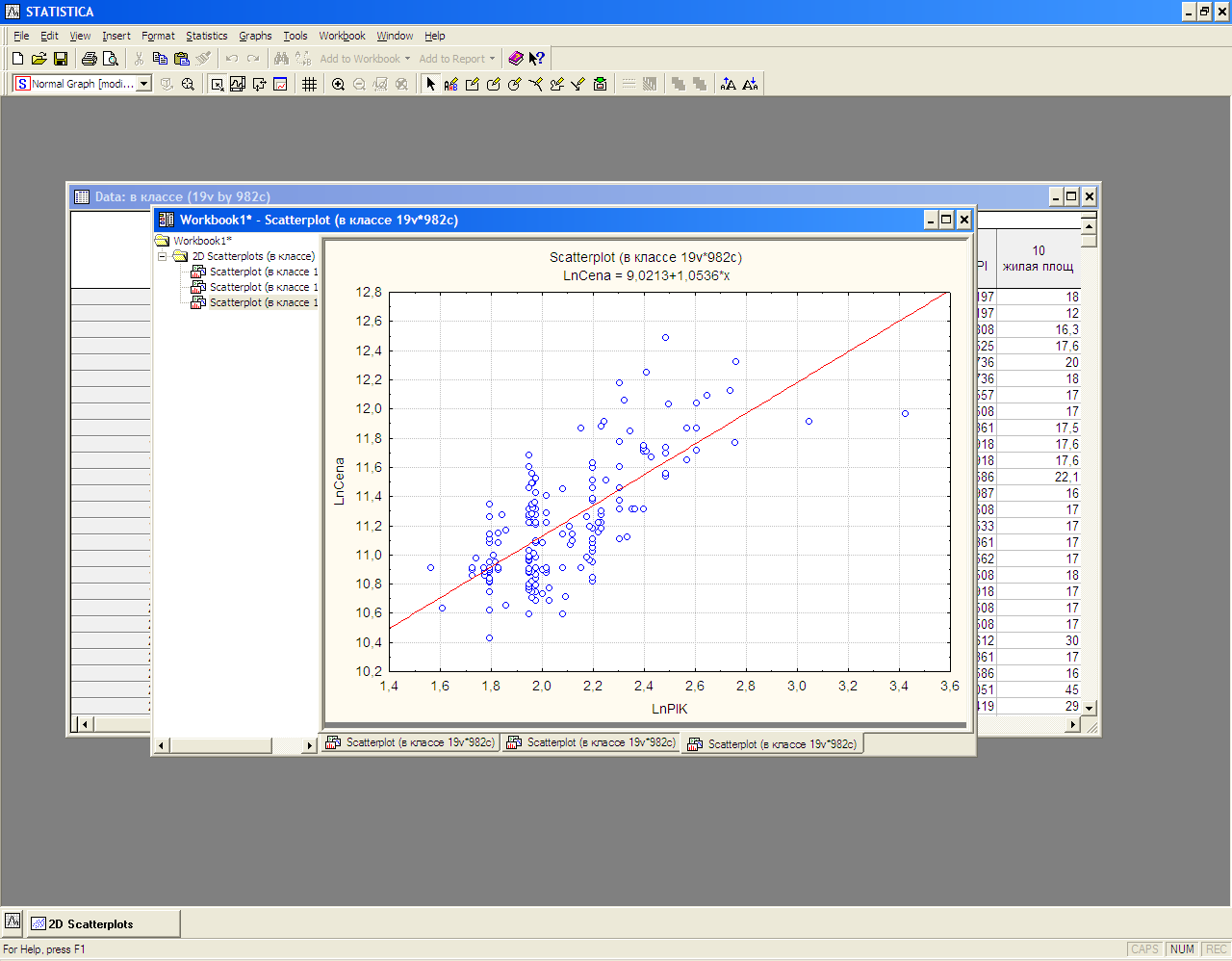
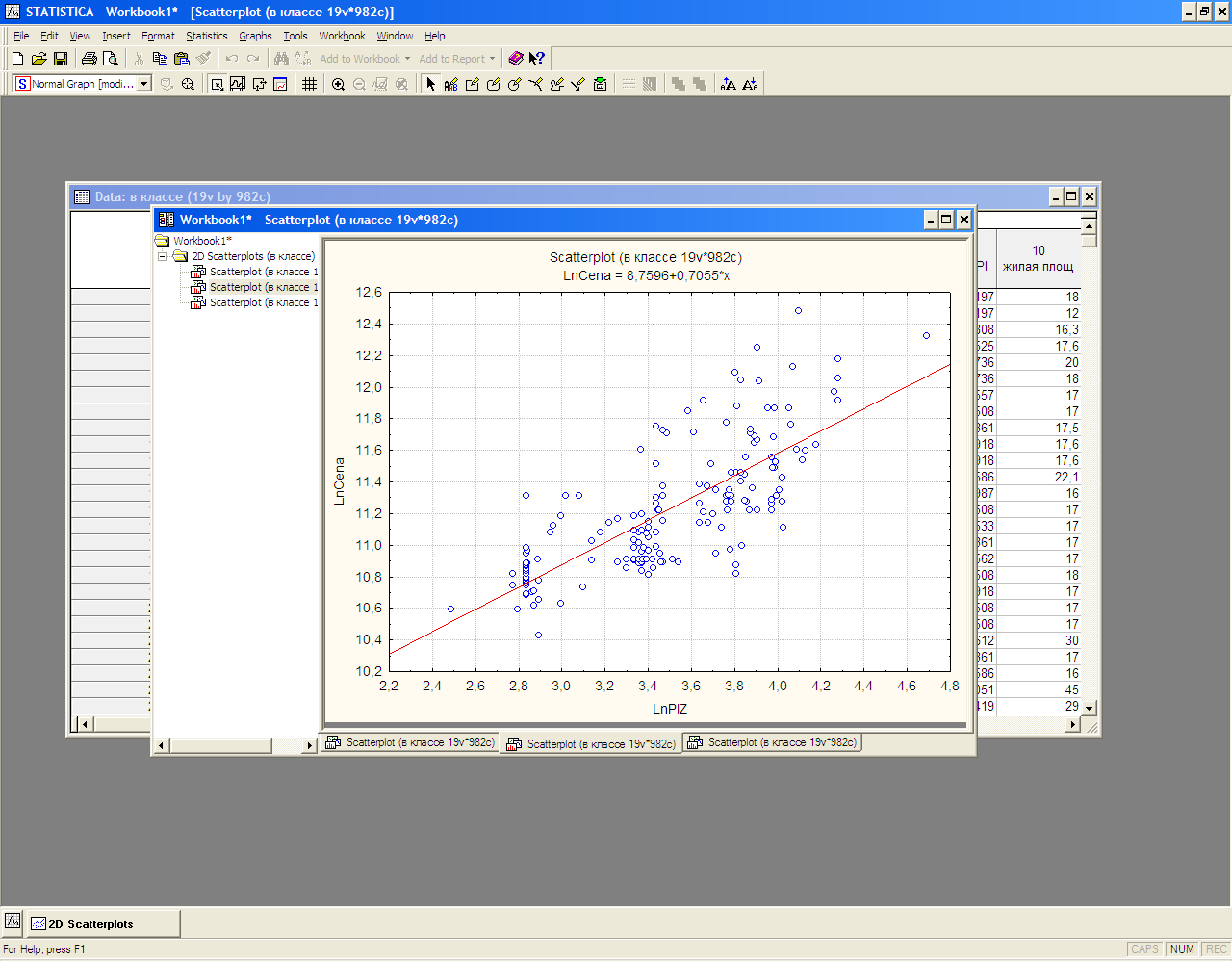
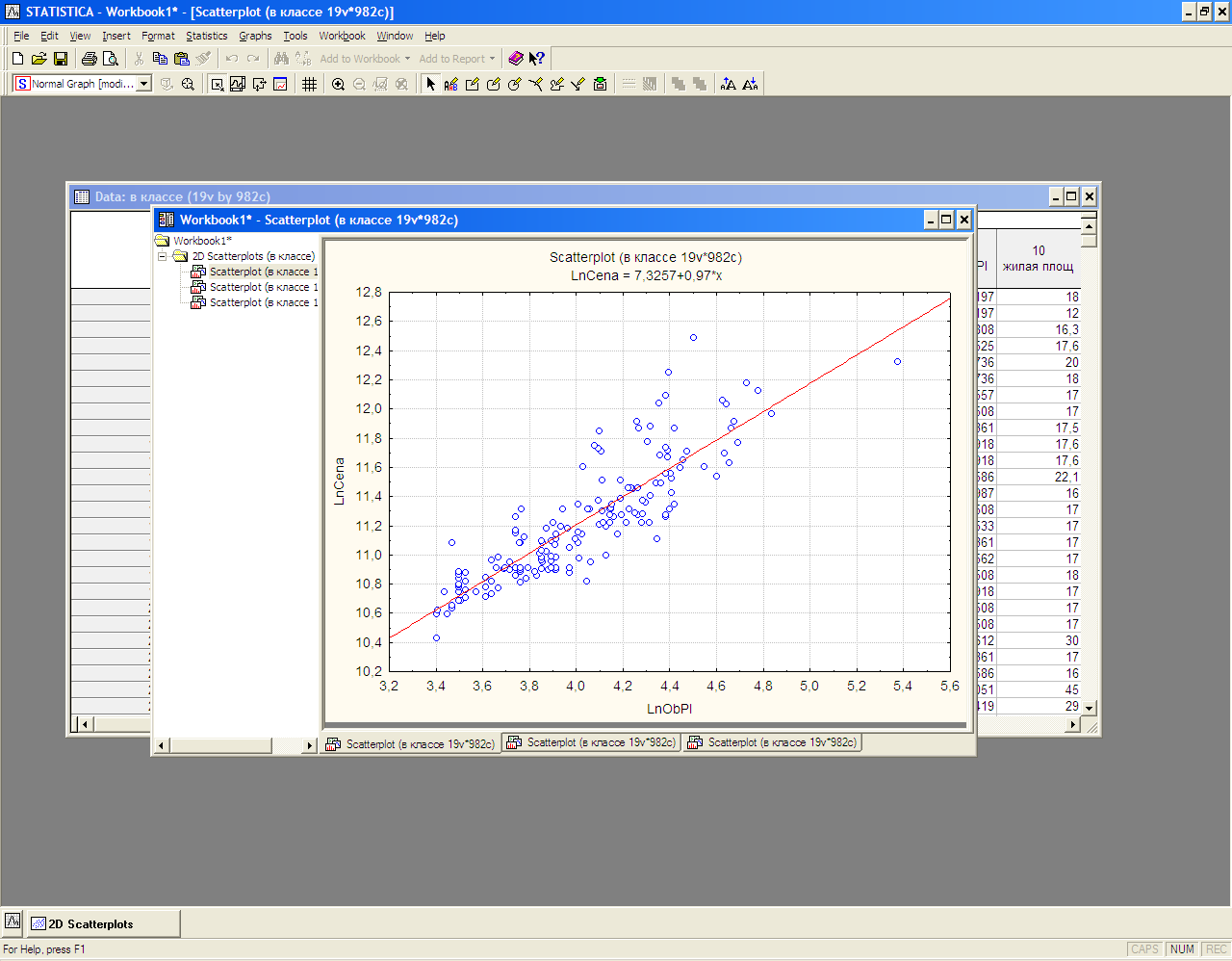
Рис. 3.

Будем строить модель в логарифмической форме. Для этого следует выполнить следующую последовательность команд: Statistics/Multiple regression и в открывшемся диалоговом окне определить эндогенную и экзогенные переменные (рис.4).

Рис.4 Выбор переменных модели

В качестве эндогенной переменной определена переменная LnCena, в качестве экзогенных: LnPlZ (логарифм жилой площади), LnPlK (логариф площади кухни) и фиктивные переменные: дом (1 – если дом кирпичный, 0 - иначе), этаж (1, если квартира расположена на крайних этажах, 0 - иначе), elit. Последняя переменная имеет несколько категорий и определяется вами самостоятельно. В данном примере она принимает следующие значения. Если стоимость квадратного метра квартиры много меньше средней стоимости квадратного метра по выборке, то переменной присваиваются значения -1 или -2 в зависимости от этой разницы, если же квадратный метр больше среднего значения по выборке – то 1 или 2. Во всех остальных случаях значение переменной полагается равным 0. По своему содержанию эта переменная несет такую смысловую нагрузку, как состояние квартиры, отраженное в цене квадратного метра.

Получены следующие результаты (после нажатия OK следует перейти на вкладку Advanced/Summury:Regression Results ):

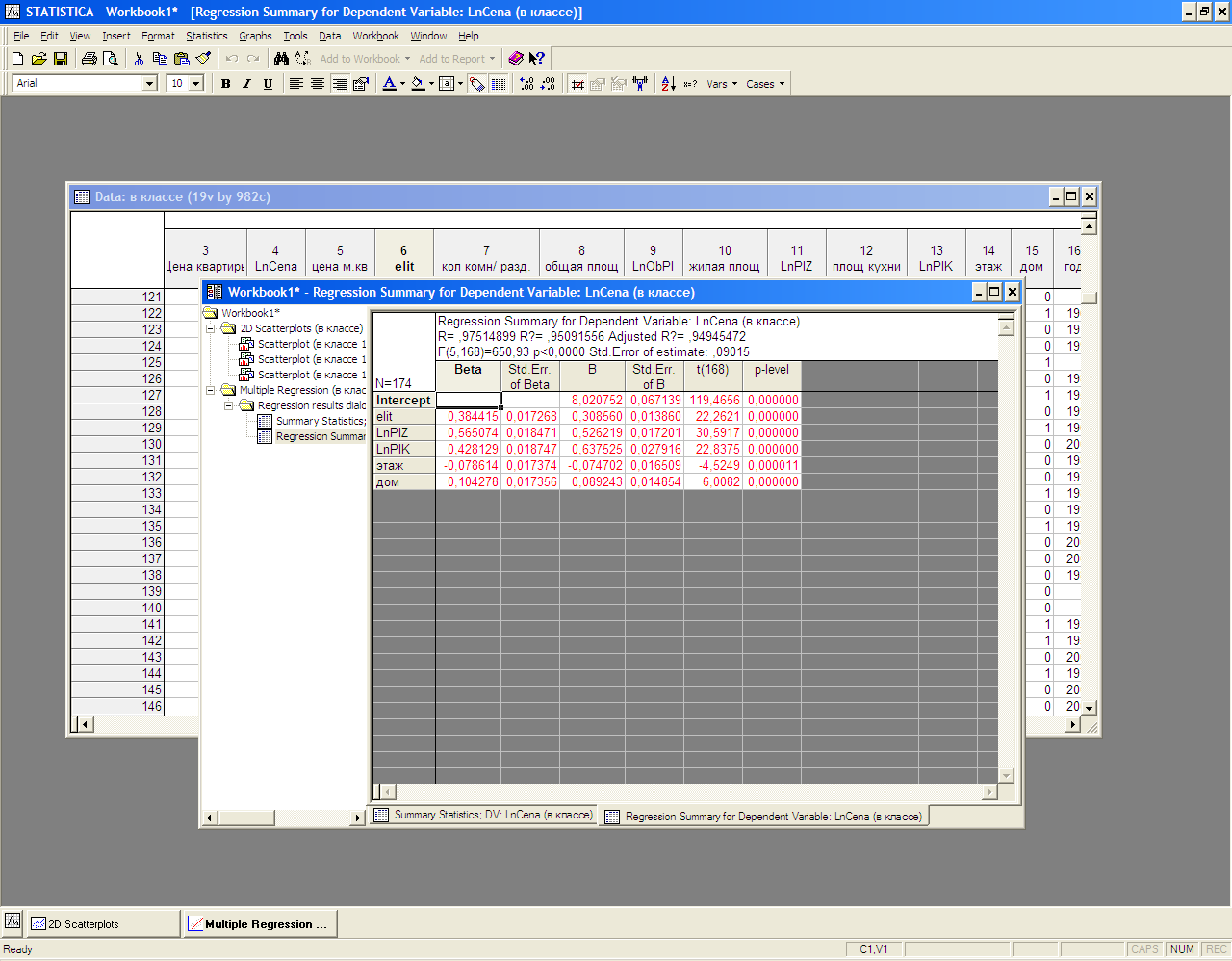
В заголовки таблицы результатов представлены множественный коэффициент корреляции R=0.975, коэффициент детерминации R²=0,950 и скорректированный коэффициент детерминации adjusted R²=0,949.

Третий столбец содержит оценки коэффициентов регрессии, второй – стандартная ошибка коэффициентов, далее значение t-статистики и p-значение.

Как видно из таблицы результатов все коэффициенты являются статистически значимыми на 5% уровне, о чем свидетельствуют высокие значения t-статистики и p-level<0,05. в целом модель является адекватной: соответствующая F- статистика = 650,93, p-level<0,05/ высокие значение коэффициента детерминации (0,95) и скорректированного коэффициента детерминации (0,94) также свидетельствуют в пользу об удовлетворительном качестве модели.

Проанализируем остатки модели. Целью данного анализа является проверка выполнимости модельных предположений: отсутствие автокорреляции и гетероскедастичности в остатках и соответствие распределения остатков нормальному закону. проверка автокорреляции выполняется на основе критерия Дарбина-Уотсона. Для этого в окне «Multiple Regression Results» рис. следует перейти на вкладку «Residual/Assumption/Prediction» и выполнить команду «Perform residual analysis».

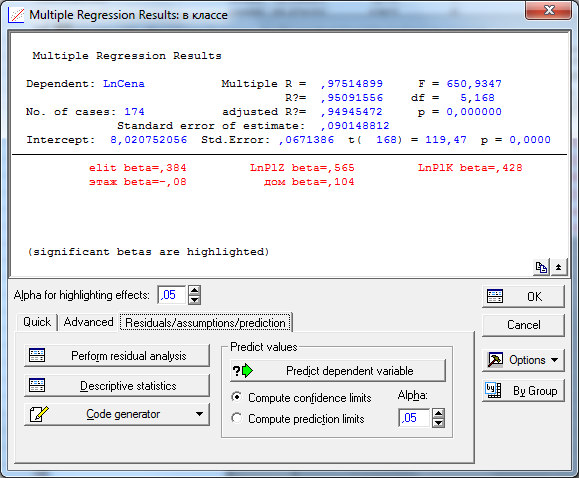
В новом окне «Residual Analysis» на вкладке «Advanced» выполнить «Darbin-Watson statistic» (рис.).