22.2.2. Метод Ньютона

Этот метод является модификацией метода простой итерации и часто называется методом касательных. Если f(x) имеет непрерывную производную, тогда, выбрав в (22.3) у/(x) = 1/ f (x), получаем эквивалентное уравнение

x = x - f (x)/ f'(x) = (p(x), в котором q = (?'(x*) = 0. Поэтому скорость сходи­мости рекуррентной последовательности метода Ньютона

x_k = x_k-1 - = (( x_k-1) (22.6)

^{f (x}k-1⁾

вблизи корня очень большая, погрешность очередного приближения примерно равна квадрату погрешности предыдущего.

Из (22.6) видно, что этот метод одношаговый (m=1) и для начала вы­числений требуется задать одно начальное приближение x₀ из области схо­димости, определяемой неравенством

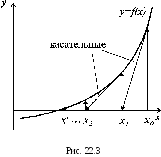
f ■ f"|/(f 'f < 1. Метод Ньютона полу­чил также второе название метод касательных благодаря геометрической иллюстрации его сходимости, представленной на рис. 22.3. Этот метод позво­ляет находить как простые, так и кратные корни. Основной его недостаток -малая область сходимости и необходимость вычисления производной f(x).

22.2.3. Метод секущих

Данный метод является модификацией метода Ньютона, позволяющей избавиться от явного вычисления производной путем ее замены приближен­ной формулой (22.2). Это эквивалентно тому, что вместо касательной на рис. 22.3 проводится секущая. Тогда вместо процесса (22.6) получаем

xk = xk-1 - _f( {^-(^ _h) = Ф(xk-1) (22.7)

здесь h - некоторый малый параметр метода, который подбирается из условия наиболее точного вычисления производной. Метод одношаговый (m=1), и его условие сходимости при правильном выборе h такое же, как у метода Ньютона.

22.2.4. Метод Вегстейна

Этот метод является модификацией предыдущего метода секущих. В нем предлагается при расчете приближенного значения производной по раз­ностной формуле использовать вместо точки x_k-1 - h в (22.7) точку x_k-2 , по­лученную на предыдущей итерации. Расчетная формула метода Вегстейна:

x_k = x_k-1 - ^f((X;^{-xk-1 -xk-})⁾ = ф(x_k_ 1,x_k-) (22.8)

Метод является двухшаговым (m=2), и для начала вычислений требу­ется задать два начальных приближения x₀, x₁. Лучше всего x₀ = а, x₁ = )

(см. рис. 22.1). Метод Вегстейна сходится медленнее метода секущих, одна­ко, требует в два раза меньшего числа вычислений f(x) и за счет этого оказы­вается более эффективным. Этот метод иногда называется улучшенным ме­тодом простой итерации и в применении к записи уравнения в форме (22.2) имеет вид

к-i

i ­

^xk-1 -Я>^{( x}k-i)

(Р^(хк-i^{) -}(Р^(хк-2⁾

(22.9)

x

x

к-1

к-2

22.2.5. Метод парабол

Предыдущие три метода (Ньютона, секущих, Вегстейна) фактически основаны на том, что исходная функция f(x) аппроксимируется линейной за­висимостью вблизи корня и в качестве следующего приближения выбирается точка пересечения аппроксимирующей прямой с осью абсцисс. Ясно, что ап­проксимация будет лучше, если вместо линейной зависимости использовать квадратичную. На этом и основан один из самых эффективных методов - ме­тод парабол. Суть его в следующем: задаются три начальные точки x₀, x₁, x₂

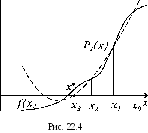
(обычно x₀ =а, x₂ = в, x₁ ^{= а}~2 ^в), в этих точках рассчитываются три зна­чения функции y = f (x), y₀, y₁, y₂ и строится интерполяционный многочлен второго порядка (рис. 22.4), который удобно записать в форме

_/t

P₂ = a( x - x₂) + b( x - x₂) + c = az + bz + c. (22.10)

Коэффициенты этого многочлена вычисляются по формулам:

z=x-x2; zo=xo-x2; zi=xi-x2; c=y2;

^{a = (y0 - y2)z1 - (y1 - y2)z0 . b = (y0 - y2)zf - (y1 - y2)z02 (22 11)}

^z0^z1^(z0^-z1^{) z}0^z1^(z1^-z0⁾

Полином (22.10) имеет два корня

_{= -b±4b2 -4ac}

^Z1,2 = Z ^,

из которых выбирается наименьший по модулю z_m и рассчитывается следующая точка x₃ = x₂ + z_m, в результате получается рекуррентная формула метода парабол:

^Xk = ^Xk-1 + ^Zm ^(Xk-ь ^Xk-2^{, X}k-3⁾ = <P^(Xk-1^{, X}k^Xk-3^{) . (22.12)}

Метод трехшаговый (m=3). Скорость сходимости его больше, чем у ме­тода Вегстейна, однако, не лучше, чем у метода Ньютона вблизи корня.

22.2.6. Метод деления отрезка пополам

Все вышеописанные методы могут работать, если функция/(x) является непрерывной и дифференцируемой вблизи искомого корня. В противном слу­чае они не гарантируют получение решения. Для разрывных функций, а так­же. если не требуется быстрая сходимость, для нахождения простого корня на интервале (а, в) применяют надежный метод деления отрезка пополам. Его алгоритм основан на построении рекуррентной последовательности по следующему закону: в качестве начального приближения выбираются грани­цы интервала, на котором точно имеется один простой корень

x₀ = а, x₁ = в, далее находится его середина x₂ = ^X° + ^X1; очередная точка x₃

выбирается как середина того из смежных с x₂ интервалов [x°, x₂ ] или [x₂, x₁ ] , на котором находится корень. В результате получается следующий алгоритм метода деления отрезка пополам:

1. Вычисляем y° = /(x°), y = /(.

2. Вычисляем x₂ = (x° + x₁)/2, y₂ = /(x₂).

3. Если y° ■ У2 > °, то x° = X2, y° = У2, иначе X1 = X2, У1 = У2.

4. Если x₁ - x° > s, тогда повторять с п.2.

5. Вычисляем x* = (x° + x₁)/2.

6. Конец.

За одно вычисление функции погрешность уменьшается вдвое, то есть скорость сходимости невелика, однако метод устойчив к ошибкам округления и всегда сходится.

ЛЕКЦИЯ 23. МЕТОДЫ ОПТИМИЗАЦИИ