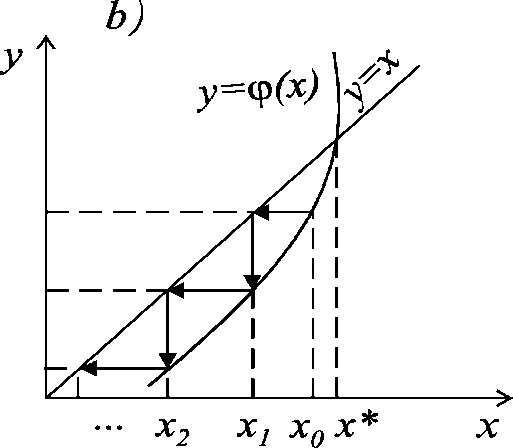- •Работает
- •1.1. История создания эвм.
- •1.3. Размещение данных и программ в памяти пэвм.
- •1.4.Файловая система хранения информации
- •1.5.Операционная система.
- •Лекция 2. Как составляются и выполняются программы в системе delphi
- •2.1. Понятие алгоритма и способы его записи
- •2.2. Общая характеристика языка Паскаль
- •2.3. Как составляется программа в системе Delphi
- •2.4. Наша первая программа реализует линейный алгоритм
- •3.1. Данные и их типы.
- •3.2. Операции над переменными основных скалярных типов
- •Алгоритмов
- •4.1. Понятие разветвляющегося алгоритма
- •4.2. Оператор условия if
- •4.3. Оператор выбора Case
- •4.4. Некоторые возможности, предоставляемые Delphi для организации разветвлений
- •Лекция 5. Составление и програмирование циклических алгоритмов
- •5.1. Понятие цикла
- •5.2. Оператор Repeat...Until
- •5.3. Оператор While...Do
- •5.4. Оператор For...Do
- •5.5. Вложенные циклы
- •5.6. Примеры некоторых часто встречающихся циклических алгоритмов Вычисление заданного члена рекуррентной последовательности
- •Вычисления сумм с использованием рекуррентной последовательности
- •6.1. Ошибки на этапе компиляции
- •6.4. Защищенные блоки
- •6.5. Некоторые стандартные типы исключительных ситуаций
- •6.6. Инициирование собственных исключительных ситуаций
- •6.7. Примеры фрагментов программ
- •Лекция 7. Составление программ с использованием массивов
- •7.1. Понятие массива
- •7.2. Некоторые возможности ввода-вывода в Delphi
- •7.3. Примеры часто встречающихся алгоритмов работы с массивами Сумма n элементов одномерного массива:
- •Произведение диагональных элементов квадратной матрицы:
- •Нахождение максимального элемента одномерного массива:
- •8.1. Статическое и динамическое распределение оперативной памяти
- •8.2. Понятие указателя
- •8.3. Наложение переменных
- •8.4. Динамическое распределение памяти
- •8.5. Организация динамических массивов
- •9.1. Понятие подпрограммы
- •9.2. Описание подпрограмм
- •9.3. Передача данных между подпрограммой и вызывающей ее программой
- •9.4. Оформление подпрограмм в библиотечный модуль
- •9.5. Примеры подпрограмм, оформленных в отдельные библиотечные модули
- •Пример программы, использующей модуль RabMas:
- •Множества
- •10.1. Понятие множества
- •10.2. Операции над множествами
- •10.3. Примеры работы с множествами
- •Interface
- •11.1. Зачем нужны строки
- •11.2. Описание переменных строкового типа «Короткие строки»
- •11.3. Основные операции над переменными строкового типа
- •11.4. Некоторые процедуры и функции обработки строк
- •11.5. Примеры алгоритмов обработки строк
- •Лекция 12. Программирование с использованием записей
- •12.1. Понятие записи
- •12.2. Операции над записями
- •12.3. Использование записей для работы с комплексными числами
- •13.1. Понятие файла
- •13.2. Операции над файлами
- •13.2.1. Типизированные файлы
- •13.2.2. Текстовые файлы
- •13.3. Подпрограммы работы с файлами
- •13.4. Компоненты tOpenDialog и tSaveDialog
- •Лекция 14. Программирование с отображением графической информации
- •14.1. Как рисуются изображения
- •14.2. Построение графиков с помощью компонента tChart
- •Лекция 15. Программирование с использованием рекурсии
- •15.1. Понятие рекурсии
- •15.2. Примеры рекурсивных вычислений
- •16.1. Организация работы с базами данных
- •16.2. Поиск в массиве записей
- •16.3. Сортировка массивов
- •16.3.1. Метод пузырька
- •16.3.2. Метод прямого выбора
- •16.3.3. Метод Шелла
- •16.3.4. Метод Хоара (Hoare)
- •17.1. Работа со списками
- •17.2. Добавление нового элемента в список на заданную позицию
- •17.3. Удаления элемента с заданным номером
- •17.4. Пример программы
- •Лекция 18. Связанные списки на основе рекурсивных данных
- •18.1. Что такое стек и очередь
- •18.2. Понятие рекурсивных данных и однонаправленные списки
- •18.3. Процедуры для работы со стеками
- •18.4. Процедуры для работы с односвязными очередями
- •18.5. Работа с двухсвязными очередями
- •18.6. Процедуры для работы с двусвязными очередями
- •19.1. Основные понятия и определения
- •19.2. Прямые методы решения слау
- •19.3. Итерационные методы решения слау
- •20.1. Зачем нужна аппроксимация функций?
- •20.3. Какие бывают многочлены и способы интерполяции?
- •20.4. Что такое среднеквадратичная аппроксимация?
- •20.5. Метод наименьших квадратов (мнк)
- •21.1. Формулы численного дифференцирования
- •21.2. Формулы численного интегрирования
- •22.1. Как решаются нелинейные уравнения
- •22.2. Итерационные методы уточнения корней
- •22.2.2. Метод Ньютона
- •23.1. Постановка задач оптимизации, их классификация
- •23.2. Методы нахождения минимума функции одной переменной
- •24.1. Задачи для обыкновенных дифференциальных уравнений
- •24.2. Основные положения метода сеток для решения задачи Коши
- •24.3. Многошаговые схемы Адамса
- •Литература
22.1. Как решаются нелинейные уравнения
Математической моделью многих физических процессов является функциональная зависимость y=f(x). Поэтому задачи исследования различ- ных свойств функции f(x) часто возникают в инженерных расчетах. Одной из таких задач является нахождение значений x, при которых функция f(x) обра- щается в нуль, т.е. решение уравнения f(x) =0. (22.1)
Точное решение удается получить в исключительных случаях, и обычно для нахождения корней уравнения применяются численные методы. Решение уравнения (22.1) при этом осуществляется в два этапа:
Приближенное определение местоположения, характер и выбор интересующего нас корня.
Вычисление выбранного корня с заданной точностью s.
Первая задача решается графическим методом: на заданном отрезке [a, f] вычисляется таблица значений функции с некоторым шагом h, строится ее график, например, с помощью компонента Chart и определяются интервалы (ai, Д) длиной h, на которых находятся корни.
На рис. 22.1 представлены три наиболее часто встречающиеся ситуации:
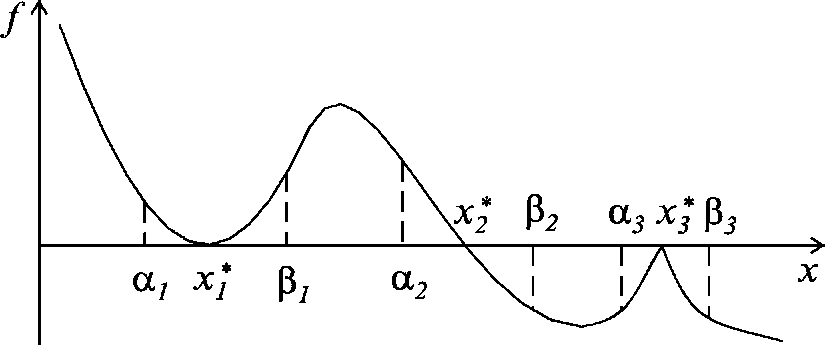
Рис.22.1
а) кратный корень: f'(x*) = 0, f (а1) ■ f (Д) > 0;
б) простой корень: f'(x*) ф 0, f(а2) ■ f(Д2) < 0;
в) вырожденный корень: f'(x*) не существует, f (а3) ■ f (Д3) > 0.
Как видно из рис. 22.1, в случаях а) и в) значение корня совпадает с точкой экстремума функции и для нахождения таких корней рекомендуется использовать методы поиска минимума функции, описанные в лекции 2з.
На втором этапе вычисление значения корня с заданной точностью осуществляется одним из итерационных методов. При этом, в соответствии с общей методологией m-шагового итерационного метода, на интервале (а, в), где находится интересующий нас корень x , выбирается m начальных значений x0, x1, xm-1 (обычно x0=a, x1=)), после чего последовательно находятся члены (xm, xm+1, xn-, xn) рекуррентной последовательности порядка m по правилу xk = ф(xk-1, xk-m) до тех пор, пока |xn -xn-1| <s. Последнее
*
xn выбирается в качестве приближенного значения корня (x *xn).
Многообразие методов определяется возможностью большого выбора законов ф. Наиболее часто используемые на практике описаны ниже.
22.2. Итерационные методы уточнения корней
22.2.1. Метод простой итерации
Очень часто в практике вычислений встречается ситуация, когда уравнение (22.1) записано в виде разрешенном, относительно x:
x = < (x). (22.2)
Заметим, что переход от записи уравнения (22.1) к эквивалентной запи- си (22.2) можно сделать многими способами, например, положив <(x) = x + у/( x) f (x), (22.3)
где ц/(x) - произвольная, непрерывная, знакопостоянная функция (часто достаточно выбрать \\i=consi). В этом случае корни уравнения (22.2) являются также корнями (22.1), и наоборот. Исходя из записи (22.2) члены рекуррентной последовательности в методе простой итерации вычисляются по закону
xk = ф(xk-1), k = 1,2,... . (22.4)
Метод является одношаговым, так как последовательность имеет первый порядок (m=1) и для начала вычислений достаточно знать одно начальное приближение x0 = а илиx0 = ) или x0 = (а + ))/2.
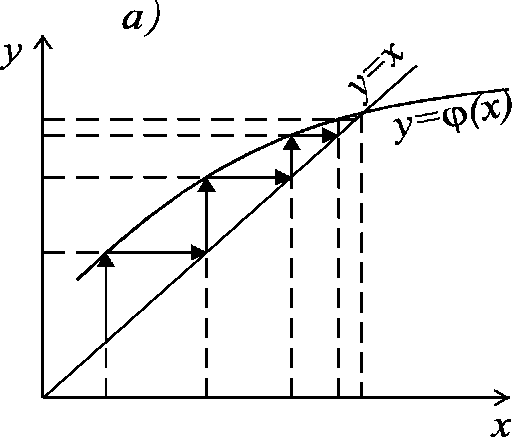
Геометрическая иллюстрация сходимости и расходимости метода простой итерации представлена на рис. 22.2, a), b), из которого видно, что метод не всегда сходится к точному решению.
Условием сходимости метода простой итерации, если ф(x) дифференцируема, как показывает анализ графиков, является выполнение неравенства
|ф'(%)| < 1, для любого % = (а, )), x* е (а, )). (22.5)
Максимальный интервал (а, )), для которого выполняется неравенство (22.5), называется областью сходимости. При выполнении условия (22.5) метод сходится, если начальное приближение x0 выбрано из области сходимо-
сти. При этом скорость сходимости погрешности
x
x
к нулю
вблизи корня приблизительно такая же, как у геометрической прогрессии sk « sk-1q со знаменателем q = |(?'(x*)|, т.е. чем меньше q, тем быстрее сходимость, и наоборот. Поэтому при переходе от (22.1) к (22.2) функцию ц/(x) в (5.3) выбирают так, чтобы выполнялось условие сходимости (22.5) для как можно большей области (а, Д) и с наименьшим q. Удачный выбор этих условий гарантирует эффективность расчетов. Часто положительные результаты дает применение релаксации.