Основы термодинамики.

Число степеней свободы– это количество независимых переменных (координат), с помощью которых можно однозначно задать положение механической системы в пространстве. Число степеней свободы также равно числу независимых движений, которые может совершать механическая система. Для одноатомной молекулы газа число степеней свободыi=3, для двухатомной молекулы с жёсткой связьюi=5,для многоатомного газаi=6.

Внутренняя энергия многоатомного газаU представляет собой суммарную кинетической энергии теплового движения всех ее молекул и их потенциальной энергии взаимодействия.

Средняя энергия теплового движения молекул

Внутренняя энергия многоатомного идеального газа равна

Внутренняя энергия макросистемы зависит только от термодинамического состояния этой системы. Внутренняя энергия является однозначной функцией состояния термодинамической системы и не зависит от способа перехода этой системы в данное состояние.

Количество теплоты Q (теплота)–энергия, переданная макросистеме путем теплообмена, т.е. в результате процесса передачи энергии от одного тела другому без совершения работы. Единица количества теплоты – джоуль (Дж).

Теплоёмкостью С системы называется величина, равная отношению сообщённого системе количества тепла δQк изменению температуры системыdT

Удельная теплоёмкость с– теплоёмкость единицы массы вещества

Молярная теплоёмкость С– теплоёмкость одного моля.

С=Мс

Зная удельную или молярную теплоёмкость системы, можно определить количество теплоты, полученной системой.

Элементарная работа δА сил давления газа при малом изменении dV его объема равна

δА=рdV

где p – давление газа.

Полную работу А, совершаемую газом при изменении его объёма от V₁ доV₂ , найдём с помощью интегрирования

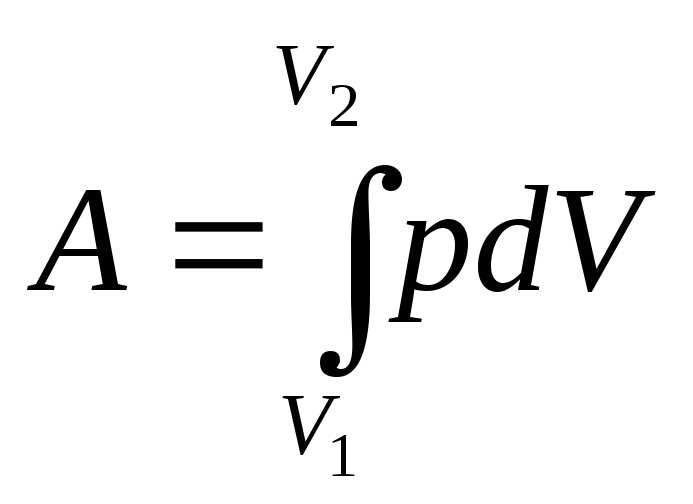
Графически работа определяется по площади заштрихованной фигуры (рис. 8)

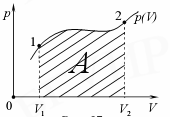
Рис. 8.

Работа зависит от процессов, протекающих в газе.

• При изохорном процессе (V= const) А=0.

• При изобарном расширении (p= const) A = p(V₂-V₁).

• При изотермическом расширении (T= const).

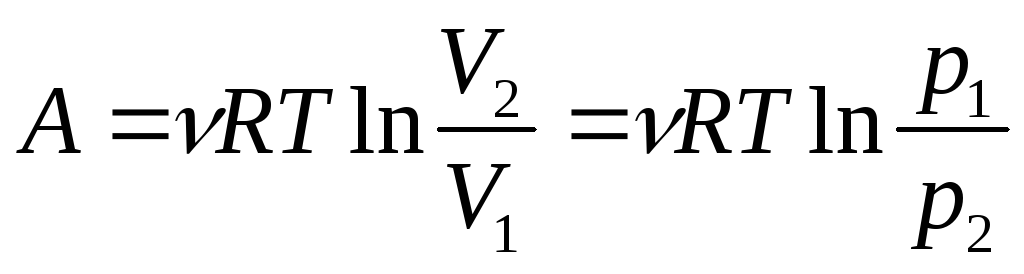В основу термодинамики положены законы, являющиеся обобщением опытных фактов. Их называют начала термодинамики.

Первое началотермодинамики – закон сохранения энергии применительно к тепловым процессам. Количество теплоты Q, переданное макросистеме, идет на изменение ее внутренней энергииdU и на совершение работы A над внешними телами.

Математическое выражение I начала термодинамики в дифференциальной форме (для элементарного термодинамического процесса) имеет вид:

δQ= dU + δA.

Применение первого начала к изопроцессам.

• Изохорный процесс. Количество теплоты, переданное газу идёт только на приращение его внутренней энергии Q=ΔU=C_vdT, гдеC_v- молярная теплоёмкость газа при постоянном объёме..

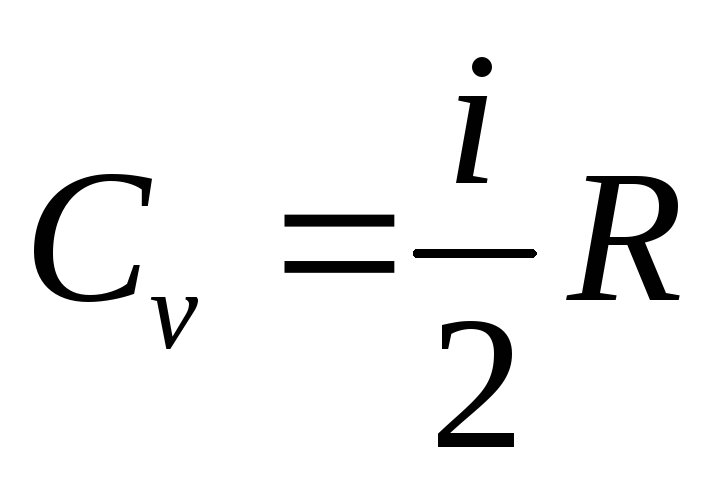• Изобарный процесс. Количество теплоты Q, переданное газу при изобарном процессе, идет на приращение внутренней энергии ΔUгаза и на совершение работы A его силами давления: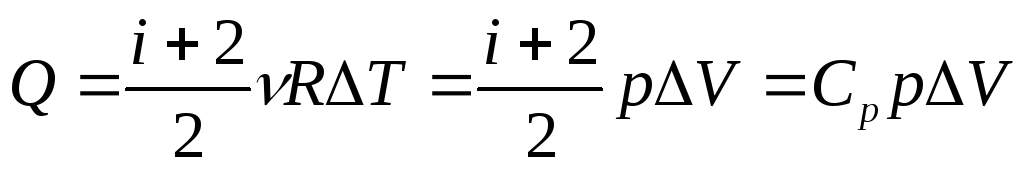, гдеС_p– теплоёмкость при постоянном давлении.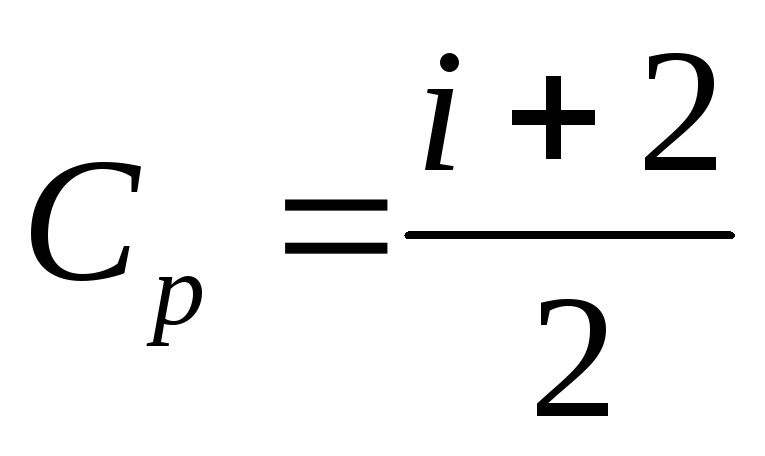. РазностьС_p-C_v=Rназывают уравнением Майера.

• Изотермический процесс. Количество теплоты Q, переданное газу при изотермическом процессе, идет только на совершение работы A силами давления этого газа: A= Q .

• Адиабатический (адиабатный) процесс. Это - процесс, протекающий без обмена с окружающей средой. Уравнение адиабатного процесса (уравнение Пуассона):

где -адиабатическая постоянная или коэффициент Пуассона.

Адиабата (рис.9, кривая 2) на координатной плоскости pVидет круче изотермы ( кривая 1).

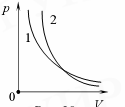
Рис. 9.

Первое начало термодинамики имеет вид: А = - ΔU, т.е. работа системы совершается за счёт уменьшения внутренней энергии.

Круговым процессом (или циклом)называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние. На рV -диаграмме цикл (рис.10) изображается замкнутой кривой, где участок 1→2 соответствует расширению, а 2→1– сжатию газа.

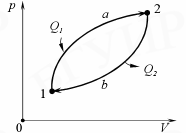
Рис. 10.

Тепловой двигатель(машина) – периодически действующее устройство, преобразующее теплоту в механическую работу. Любой тепловой двигатель

работает по круговому процессу (циклу).

Карно показал, что наиболее экономичным является двигатель, работающий по обратимому круговому циклу, состоящему из двух изотерм и двух адиабат (рис.11).

Рис. 11.

1→2 – газ изотермически (T₁=const ) расширяется, получая от нагревателя с температурой T₁количество тепла Q₁,

2→3 – газ адиабатически расширяется, охлаждаясь до температуры Т₂,

3→4 – газ изотермически (T₂=const) сжимается, отдавая холодильнику количество во теплоты Q₂;

4→1 - газ адиабатически сжимается, при этом его температура увеличивается до Т₂.

Теоремы Карно.

1.КПД цикла Карно с идеальным газом η зависит только от температуры нагревателя и температуры холодильника.

2.КПД любого теплового двигателя η₁не может превышать КПД теплового двигателя, работающего по циклу Карно в том же интервале температур:

η₁ ≤η

КПД любого теплового двигателя можно также определить, как величину, равную отношению работы А, совершённой системой, к количеству тепла, полученному от нагревателя.

II начало термодинамикиопределяет направление процессов, происходящих в природе и связанных с превращением энергии

II начало термодинамики (формулировка Р. Клаузиуса, 1850 г.): невозможен процесс, единственным конечным результатом которого был бы переход теплоты от менее нагретого тела к телу более нагретому.

II начало термодинамики (формулировка У.Томсона (Кельвина), 1851 г.):

невозможны круговые процессы, единственным и конечным результатом кото-

рых было бы превращение всего полученного тепла целиком в работу.

Энтропия системы S.Это величина, которая является функцией состояния системы. Энтропия характеризует направление протекания самопроизвольных процессов в замкнутой термодинамической системе. Дифференциал этой величины .

При переходе системы из состояния 1 в состояние 2

.

В замкнутой системе для обратимых процессов =0, для необратимых -›0.

Изменение энтропии в процессах идеального газа:

• Изохорный (V=const) ;

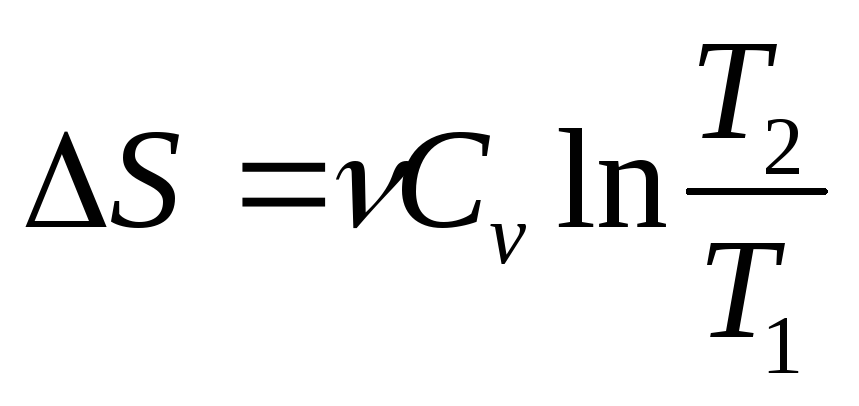• Изобарный (р=const);

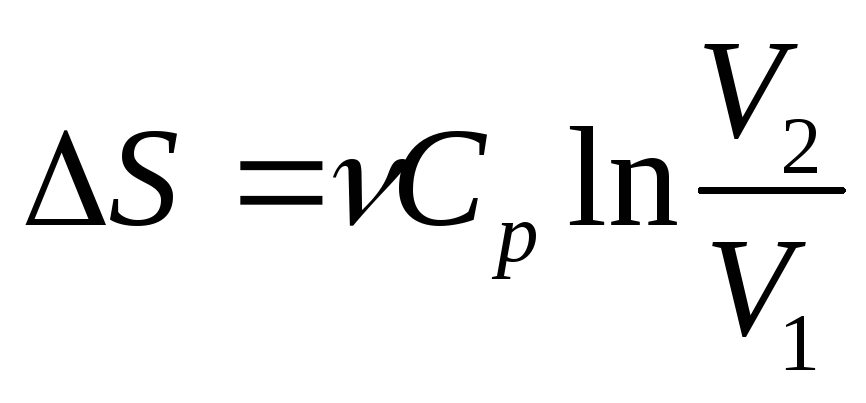• Изотермический (Т= const);

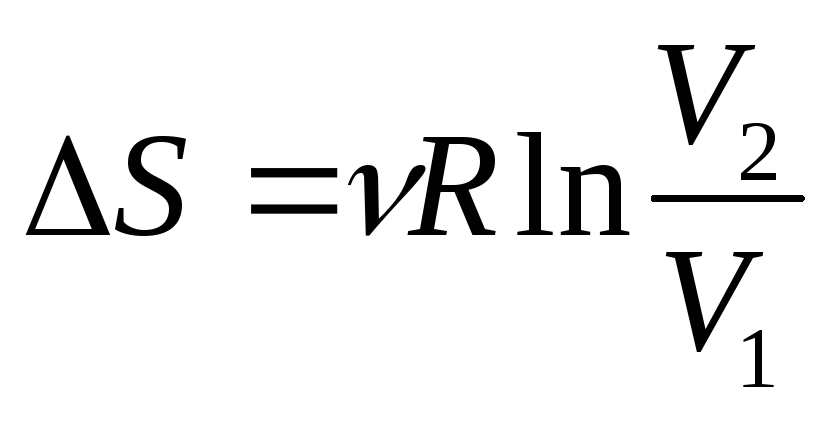• Адиабатический ΔS = 0.

Статистическое толкование энтропии. Число способов, которыми может быть реализовано данное термодинамическое состояние называетсятермодинамической вероятностью W. Как показал Больцман, энтропия пропорциональна натуральному логарифму W:

,

где k-постоянная Больцмана.

Принцип возрастания энтропии. Любой необратимый процесс в замкнутой системе протекает так, что энтропия системы возрастает.

Третье начало термодинамики.Энтропия всех систем в состоянии равновесия стремится к нулю при приближении температуры системы к абсолютному нулю.

Это утверждение носит название теоремы Нернста-Планка.