Основы молекулярной физики и термодинамики

Задача 1. Двухатомный идеальный газ с молярной массой М находится при температуре .Используя функцию распределения молекул идеального газа по относительным скоростям :, где,скорость теплового движения молекул,наиболее вероятная скорость молекул,определите (в процентах) вероятность того, что молекулы идеального газа имеют скорости теплового движения в интервале от до.

Дано:,,.

Определить:.

Решение. Число молекул, относительные скорости которых находятся в пределах отдо, определяется выражением,

где число молекул в объеме газа,– функция распределения,–заданный малый интервал скоростей. Искомая вероятность будет равна.

Учитывая малость интервала относительных скоростей, можно считать, что мы ищем величину , где,, поэтому . Подставляя числовые значения исходных величин, получим;.

Ответ: При заданных значениях М и вероятность обнаружить молекулы идеального газа со скоростями, находящимися в интервале от доравна .

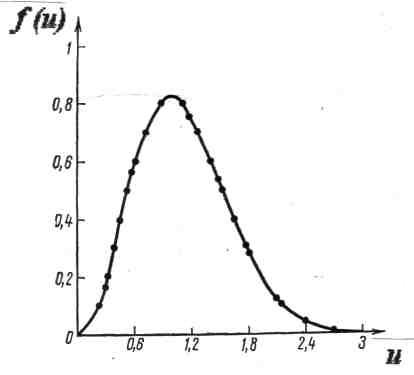
Примечание. Таким же методом можно определить вероятность того, что молекулы идеального газа имеют скорости теплового движения в любом конечном интервале относительных скоростей от до. Для этого необходимо разбить этот интервална некоторое числоинтервалов, т.е. принять, чтои провести вычисления вышеизложенным методом, т.е. найти вероятности. Искомая вероятность.

З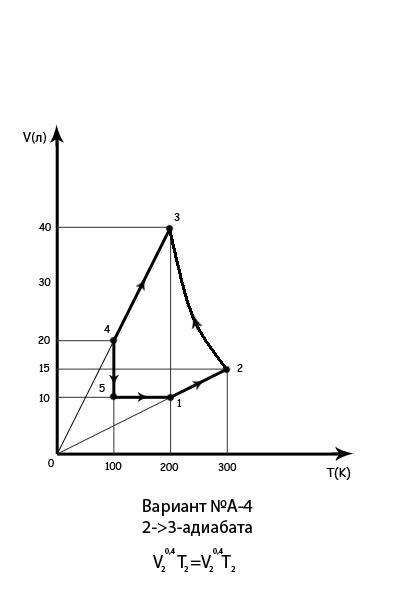адача 2. Идеальный двухатомный газ (молекулы с жесткой связью, находится в состоянии 1, параметры которого показаны на графике (см. рис.). Путем последовательного применения изопроцессов:газ переводится в исходное состояние (совершает цикл – круговой замкнутый процесс). Укажите, как называется каждый из этих изопроцессов. Для каждого из указанных процессов определите:

изменение внутренней энергии совершенную работупереданное количество теплотыизменение энтропии; а так же работу, совершенную газомза весь цикл, и КПД цикла

Дано:

Определить: и(для каждого процесса);и

Решение.

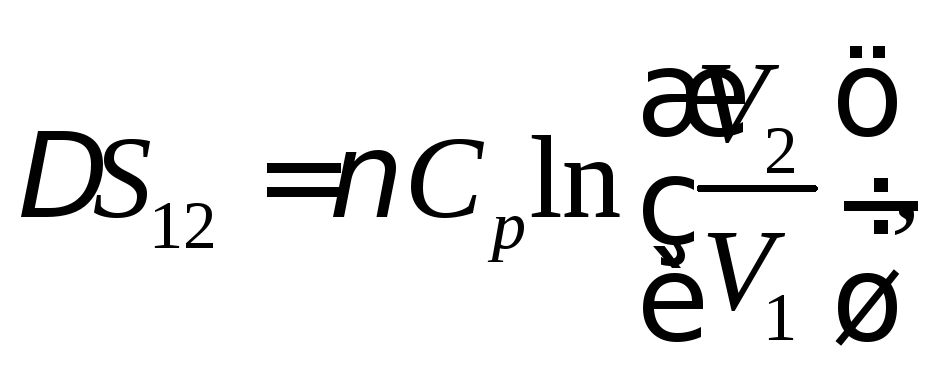1)Процесс – изобарный, из уравнения Менделеева – Клапейрона, гдеколичество вещества,молярная газовая постоянная, находимНа основании первого закона термодинамики:гдеколичество теплоты полученное газом,– изменение внутренней энергии газа,– работа газа при изобарном расширении. Изменение энтропии газа в изобарном процессе определяется выражением: гдеизобарная теплоемкость газа,– число степеней свободы (двухатомный газ). Подставив числовые значения, найдем:

,

2) Процесс – адиабатный, поэтомуиРабота расширения газа в адиабатном процессегдеизохорная теплоемкость газа, а изменение внутренней энергии газа

Подставив числовые значения, найдем:

4. Процесс изобарный.

3) Процесс изобарный. Из уравнения Менделеева – Клапейрона, находимАналогично пункту [1] определим в этом процессе изменение внутренней энергии, работу газаи изменение энтропии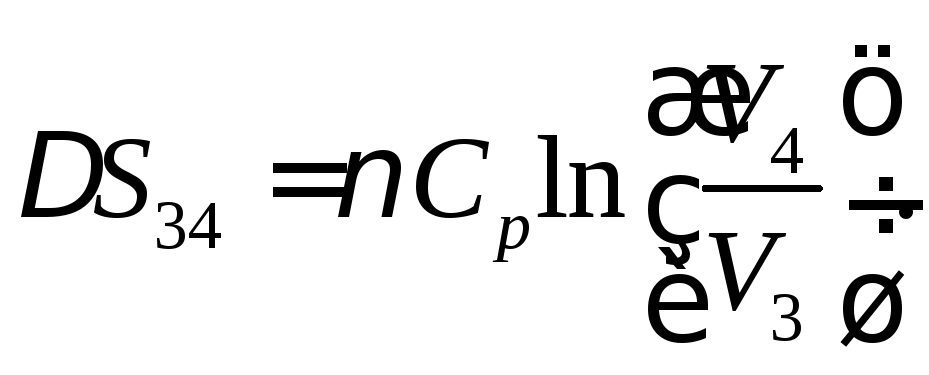Подставив числовые значения, найдем:

,

4) Процесс изотермический, поэтому изменение внутренней энергии в этом процессеколичество теплоты и работа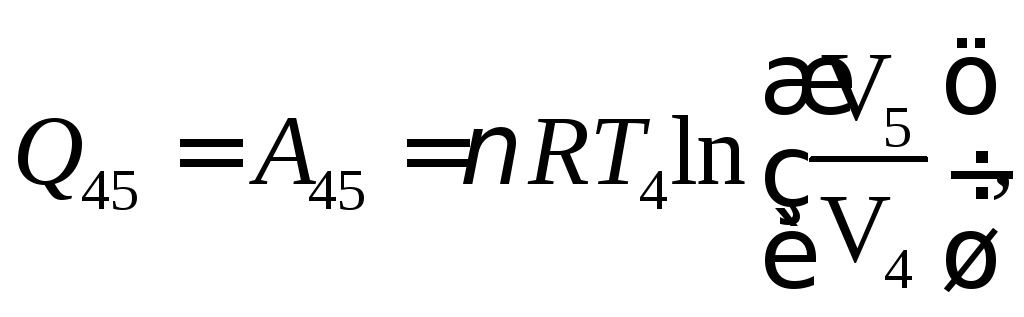а изменение энтропии

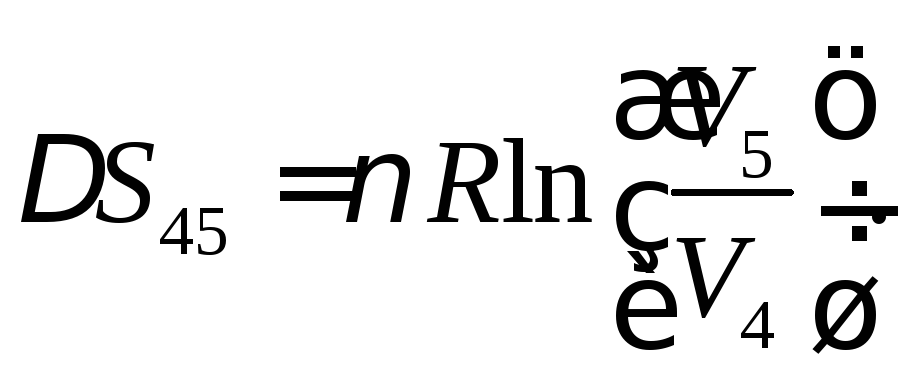Подставив числовые значения, найдем: ,

5) Процесс изохорный, поэтому работа газаколичество теплоты и изменение внутренней энергииа изменение энтропии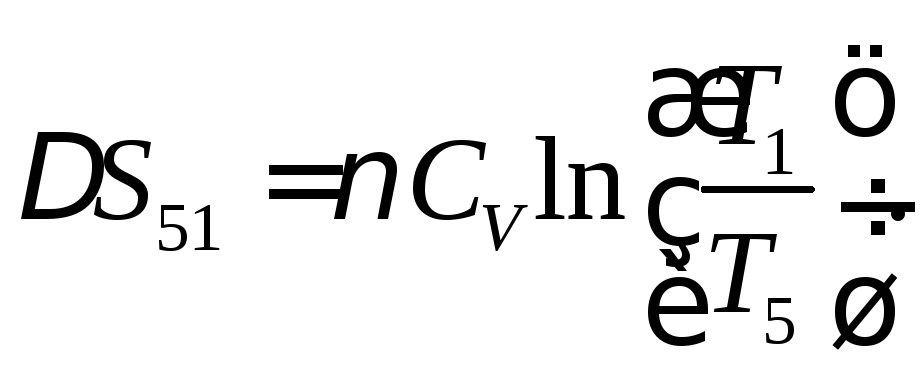Подставив числовые значения, найдем:

Работа цикла

КПД цикла или

Подставив числовые значения, можно убедиться, что для всего цикла и

Задача 3. Найти среднюю кинетическую энергию поступательного движения одной молекулы кислорода при температуре , а также кинетическую энергию поступательного движения всех молекул, содержащих кислорода.

Решение. Средняя кинетическая энергия поступательного движения одной молекулы любого газа равна

,

где – постоянная Больцмана. Подставляя в значенияk и температуры, находим

.

Кинетическую энергию поступательного движения всех молекул найдём, если умножим среднюю энергию одной молекулы на число N молекул, которое можно определить из соотношения

,

где – число Авогадро,– молярная масса кислорода. Таким образом,

,

где – универсальная газовая постоянная. Подставляя в числовые значения, находим

.

Ответ: ;.

Задача 4. Вычислить удельные теплоёмкости при постоянном объёме и при постоянном давлениинеона и водорода, принимая эти газы за идеальные.

Решение. Удельные теплоёмкости идеальных газов выражаются формулами:

, ,

где i – число степеней свободы молекулы газа;

M – молярная масса.

Для неона (одноатомный газ) и молярная масса.

Произведём вычисления:

,

.

Для водорода (двухатомный газ) и молярная масса. Тогда

,

.

Ответ: Для неона ,;

для водорода ,.

Задача 5. Разрядная трубка гелий-неонового лазера объёмом заполняется смесью гелия и неона с парциальными давлениями и, соответственно. Определить внутреннюю энергию газов.

Решение. Внутреннюю энергию идеального газа можно определить из соотношения

,

где – удельная теплоёмкость газа при постоянном объёме,T – температура газа, m – масса газа. Так как внутренняя энергия является аддитивной величиной, то для смеси газов она равна

,

где ,– массы гелия и неона,,– их удельные теплоёмкости.

Для удельной теплоёмкости идеального газа имеем формулу

,

где – молярная газовая постоянная, i – число степеней свободы молекулы газа. Так как газы гелий и неон являются одноатомными, то для них . Поэтому их удельные теплоёмкости равны

,

.

Подставляя выражение в выражение для внутренней энергии , находим

,

откуда

, .

Парциальные давления каждого газа в смеси газов удовлетворяют уравнению Клапейрона-Менделеева, т.е.

, .

Подставляя правые части уравнений в уравнения , получаем

, .

Произведём вычисления:

, .

Внутренняя энергия смеси газов равна

.

Ответ: ;;.

Задача 6. Двухатомный газ занимает объём и находится под давлением . Газ сжимается адиабатически до некоторого объёма и давления . Затем он охлаждается при до первоначальной температуры, причём его давление становится равным. Построить график этого процесса. Найти объём и давление .

Р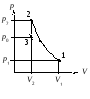ешение. Исходя из данных условия задачи, построим график процесса, который изображён на рисунке.

Запишем уравнение Клапейрона-Менделеева для газа в состояниях 1, 2 и 3:

, , ,

где m – масса газа;

 – молярная масса газа.

По условию задачи состояния 1 и 2 связаны соотношением

,

а для состояний 2 и 3 имеют место условия

, ,.

Постоянная адиабаты определяется как

,

где – удельная теплоёмкость газа при постоянном объёме;

–удельная теплоёмкость газа при постоянном давлении;

i – число степеней свободы молекулы газа.

Молекула двухатомного газа имеет 5 степеней свободы, . Следовательно, постоянная адиабаты для такого газа равна

.

Так как в уравнениях и , то левые части первого и третьего уравнений равны, т.е.

,

откуда находим объём :

.

Давление найдём из уравнения адиабаты

.

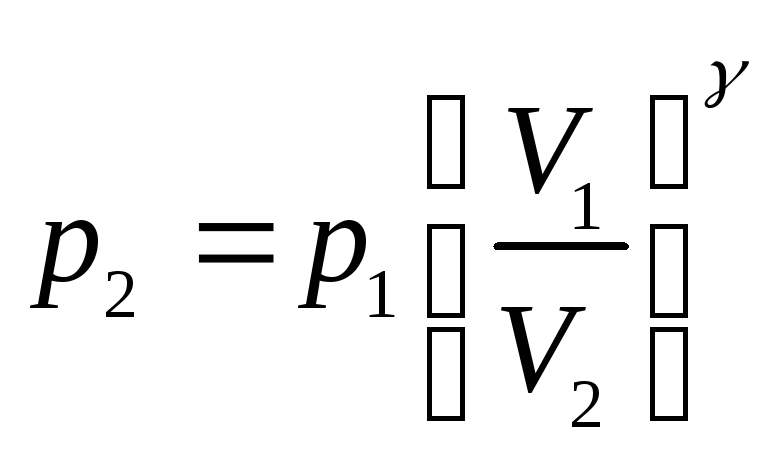Произведём вычисления:

.

Ответ: ;, где для двухатомного газа.

Задача 7. Газ, совершая цикл Карно, к.п.д. которого , при изотермическом расширении производит работу . Какова работа, совершаемая газом при изотермическом сжатии?

Решение. КПД цикла Карно определяется по формуле

,

где – теплота, полученная от теплоотдатчика, равная работе, совершаемой газом при расширении,– количество тепла, отданное газом холодильнику, равное работе, совершаемой над газом при его сжатии. Поэтому работа газа при его сжатии будет отрицательной и равной. Таким образом, из получаем

.

Ответ: .