Механические колебания.

Колебания– это процессы движения или изменения состояния, повторяющиеся в той или иной степени во времени. В процессе колебаний происходит превращение одного вида энергии в другой. Физическая природа колебаний может быть разной, различают механические, электромагнитные, электромеханические, термодинамические и т.д. Колебания различной физической природы обладают общностью закономерностей и свойств. Поэтому часто любые колебательные системы называют осцилляторами.

По характеру внешнего воздействия колебания делятся на: - свободные (собственные) колебания, возникающие в результате кратковременного внешнего воздействия. В свою очередь различают свободные незатухающие колебания и свободные затухающие колебания;

Вынужденныминазываются колебания, при которых для поддержания незатухающих колебаний к системе непрерывно или периодически подводится энергия от внешнего источника. В зависимости от способа поддержания незатухающих колебаний различают: вынужденные колебания под действием периодической силы,автоколебания, параметрические колебания и т. д.

По промежуткам времени, через которые состояние колебательной системы повторяется, колебания делятся на периодические и непериодические. Периодическими называют колебания, при которых состояние колебательной системы повторяется через одинаковые промежутки времени, т.е. значения всех величин, определяющих состояние колебательной системы, повторяются через равные промежутки времени.

Свободные незатухающие колебания.

Отклонение xколебательной системы от положения равновесия при малых колебаниях удовлетворяет уравнению свободных гармонических колебаний

,

решением которого является гармоническая функция

,

где А– амплитуда колебаний;

φ₀ – начальная фаза;

ω₀ - циклическая частота колебаний.

Период колебаний Т – промежуток времени, в течение которого колебательная система совершает одно полное колебание, т.е. приходит в начальное состояние:

,

где N–полное число колебаний за промежуток времени Δt,ν– линейная частота.

Скорость v и ускорение aматериальной точки, совершающей гармонические колебания (гармонического осциллятора):

,

Пружинный маятник – идеальная колебательная система, состоящая из тела, рассматриваемого в виде материальной точки, закрепленного на одном конце легкой пружины, другой конец которой неподвижен в некоторой инерциальной системе отсчета.

.

Период колебаний пружинного маятника массы mс жёсткостьюk, равен

.

Математический маятник – идеальная колебательная система, состоящая из легкой нерастяжимой нити длины l, один конец которой фиксирован (точка подвеса), а на другом ее конце закреплено тело, рассматриваемое в виде материальной точки.

Период колебаний математического маятника равен

.

Физический маятник – идеальная колебательная система в виде абсолютно твердого тела, насаженного на горизонтальную неподвижную ось, не проходящей через центр тяжести этого тела. (Рис. 2). Сила трения в оси подвеса (Oz,) тела отсутствует.

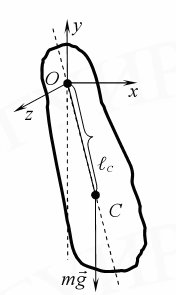
Рис.2.

Период колебаний физического маятника равен

,

где I– момент инерции маятника относительно оси, проходящей через точку подвеса маятника и перпендикулярной плоскости колебаний;

l – расстояниеOC от точки подвеса до центра масс маятника.

Приведённая длина физического маятника:. Используя приведенную длину, формуле периода колебаний физического маятника можно придать вид, аналогичный периоду математического маятника:

.

Кинетическая энергия гармонического осциллятора:

.

Потенциальная энергия гармонического осциллятора:

.

Полная энергия гармонического осциллятора:

.

Средние значения кинетической и потенциальной энергий гармонического осциллятора:

.

Результатом сложения гармонических колебаний, происходящих с одинаковой частотой в одном направлении, является также гармоническое колебание с амплитудой

и начальной фазой

,

где A₁,A₂,φ₁, φ₂– амплитуды и начальные фазы складывающихся колебаний.

Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях

,

имеет вид:

а) прямой , если разность фаз;

б) прямой , если разность фаз;

в) эллипса , если разность фаз;

г) окружности , если разность фази амплитуды равны:;

Свободные затухающие колебания.

Уравнение затухающих колебаний имеет вид

,

решением которого является функция

,

где – амплитуда затухающих колебаний;

А₀– начальная амплитуда колебаний (в момент);

φ₀ – начальная фаза;

β– коэффициент затухания.

–циклическая частота затухающих колебаний.

ω₀– циклическая частота свободных колебаний без трения.

Время релаксации системы, совершающей затухающие колебания:

.

Логарифмический декремент затухания:

,

где – период затухающих колебаний;

N_e– число колебаний за времяτ, в течение которого амплитуда уменьшается вeраз.

Добротность затухающей колебательной системы:

.

Вынужденные колебания.

Происходят под действием вынуждающей силы, изменяющейся по гармоническому закону f=f_ocosωt.

Уравнение вынужденных колебаний:

,

решением которого является функция

,

где ω– частота вынуждающей силы;

ω ₀– частота свободных колебаний без трения;

– амплитуда вынужденных колебаний;

– смещение по фазе от вынуждающей силы.

При приближении частоты вынуждающей силы ω к собственной частоте колебаний системы ω₀наблюдается явление резкого возрастания амплитуды колебаний, которое называетсярезонансом (рис. 3 )

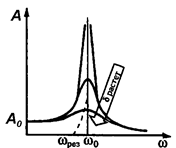
Рис.3

Резонансная частота

.

Резонансная амплитуда

.

Волны.

Волновое уравнение

,

где – отклонение точек среды от положения равновесия;

v– фазовая скорость распространения волны (колебаний среды).

Любая функция вида

является решением волнового уравнения и представляет суперпозицию двух волн, распространяющихся в направлении оси X(u₁) и в противоположном направлении (u₂).

Плоская гармоническая бегущая волна:

,

где u(x,t) – смещение точки среды, характеризуемой радиус-векторомxв момент времениt;

A₀– амплитуда волны;

–циклическая частота волны;

k– волновой вектор;

φ₀– начальная фаза волны.

Сферическая гармоническая волна:

,

где – волновое число;

λ– длина волны.

Длина волны λ фазовая скорость распространения волны vи частота волны ν связаны соотношением

.

Связь разности фаз колебаний с расстоянием Δxмежду точками среды, отсчитанным в направлении распространения колебаний:

.

Групповая скорость:

.

Скорость продольных волн в упругой среде:

,

где E– модуль продольной упругости (модуль Юнга) среды;

ρ– плотность среды.

Скорость поперечных волн в упругой среде:

,

где G– модуль сдвига среды.

Скорость звуковых волн в газообразной среде:

,

где p– давление газа;

ρ– плотность газа;

γ– показатель адиабаты.

Частота ωзвуковой волны, воспринимаемая движущимся наблюдателем (эффект Допплера):

,

где ω₀– частота звуковой волны, воспринимаемая покоящимся относительно источника наблюдателем;

v– скорость звуковой волны в неподвижной среде;

u_н– скорость движения наблюдателя относительно среды;

u_и– скорость движения источника волн относительно среды;

–единичный вектор, направленный от источника к наблюдателю;

k– волновой вектор;

θ_н– угол между векторамиu_ниk;

θ_и– угол между векторамиu_ииk.

Частота ωэлектромагнитной волны, воспринимаемая наблюдателем, движущимся вдоль направления распространения волны со скоростьюv(продольный оптический эффект Допплера):

,

где ω₀– частота электромагнитной волны, воспринимаемая покоящимся относительно источника наблюдателем;

c– скорость электромагнитных волн (света).

Частота ωэлектромагнитной волны, воспринимаемая наблюдателем, движущимся перпендикулярно направлению распространения волны со скоростьюv(поперечный эффект Допплера):

.