Краткие теоретические сведения и основные формулы Физические основы классической механики

Механика– раздел физики, изучающий простейшую форму движения материи – механическое движение. Механическое движение – изменение положения тела или его частей в пространстве относительно других тел во времени.

Материальная точка(частица) – это тело, размерами которого в условиях данной задачи можно пренебречь. Любое протяженное тело или систему таких тел можно рассматривать как систему материальных точек. Система тел – это совокупность тел, выбранная для исследования в данной задаче.

Абсолютно твердое тело– это тело, деформацией которого в условиях данной задачи можно пренебречь.

Основная задача механики– выявление общих законов и закономерностей механического движения, на основе которых можно предсказать характер движения механической системы и определить ее состояние (указать положение в пространстве и скорость всех ее частиц) в любой момент времени.

Механику в зависимости от того интересуют нас или нет причины изменения движения тела, условно делят на два раздела:

– кинематика – раздел механики, изучающий механическое движение тел без учета причин, обусловивших данное движение.

– динамика – раздел механики, изучающий механическое движение с учетом причин, обусловивших это движение. Часть динамики, изучающую условия равновесия, называют статикой. Движение твердого тела, при котором любая прямая, жестко связанная с

этим телом, движется параллельно самой себе, называется поступательным. При поступательном движении тело не изменяет свою ориентацию в пространстве.

Вращательнымдвижением вокруг оси называют такое движение твердого тела, при котором все его точки описывают окружности, плоскости которых параллельны между собой и перпендикулярны неподвижной прямой, содержащей центры данных окружностей. Эту прямую называют осью вращения.

Кинематика частицы и абсолютно твердого тела

Движение материальной точки по произвольной траектории на малом участке может рассматриваться как равномерное и прямолинейное. Мгновенная скорость vи мгновенное ускорениеaматериальной точки определяются как:

, ,

где R– радиус-вектор материальной точки M в рассматриваемой системе координат.

Скорость vвсегда направлена по касательной к траектории движения.

Величина средней скорости на малом участке:

,

где – путь, пройденный точкой за времяt,

–перемещение радиус-вектора Rза это же время.

Величина среднего ускорения определяется аналогично:

.

Если известна зависимость ускорения от времени, то скорость вычисляется по формуле

,

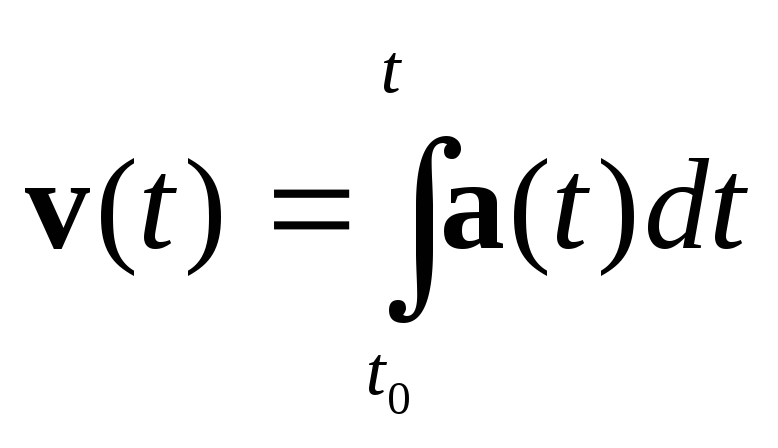а радиус-вектор материальной точки по аналогичной формуле

.

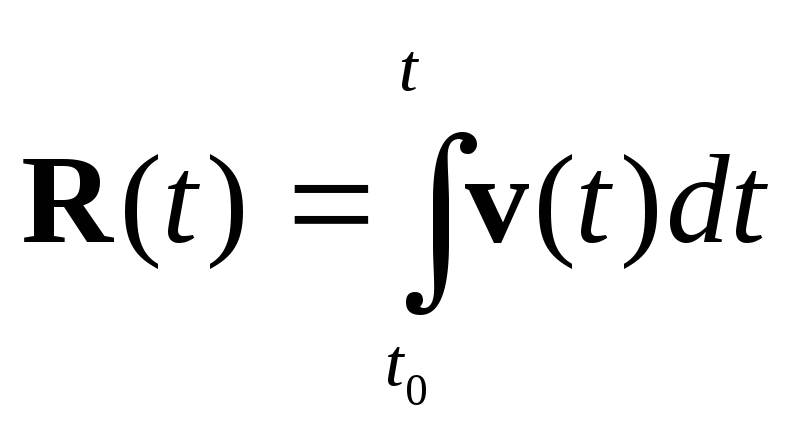Полное ускорение при движении точки по произвольной траектории разлагается на сумму тангенциального ускорения a_вдоль касательной к траектории в данной точке и нормального ускоренияa_n, перпендикулярного этой касательной:

.

Движение материальной точки по окружности радиуса Rхарактеризуется угловой скоростьюи угловым ускорением:

,

Если известна зависимость углового ускорения от времени, то угловая скорость вычисляется по формуле

,

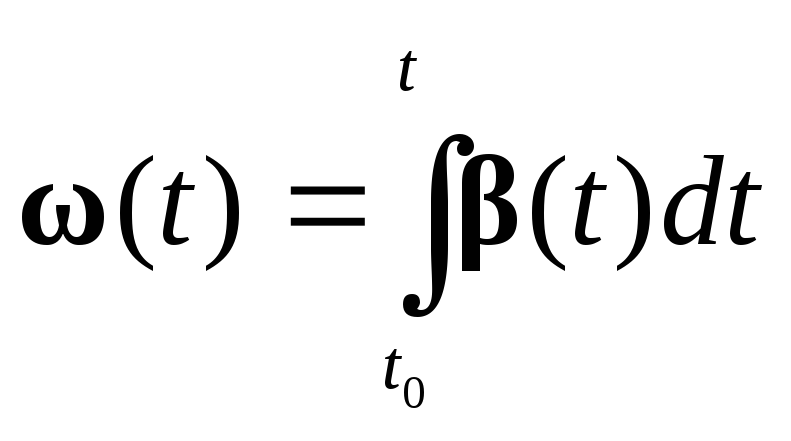а угол, на который повернётся материальная точка от начального положения, – по аналогичной формуле

.

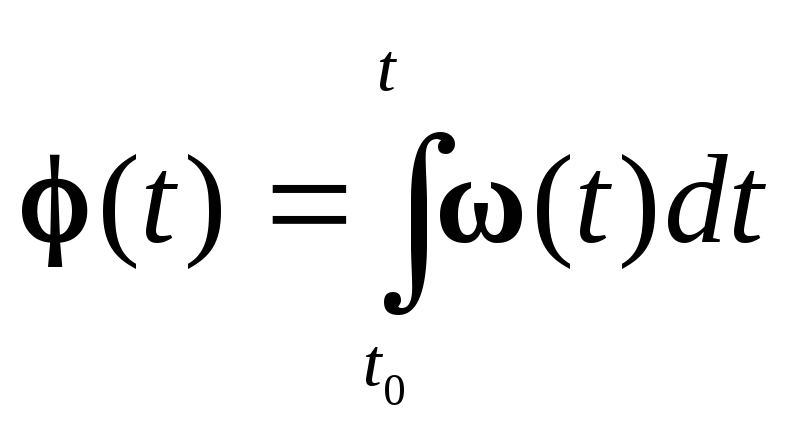Угловая скорость указывает направление вращательного движения по окружности, соответствующее закручиванию правого винта. При движении по окружности связь между линейными и угловыми скоростями и ускорениями задаётся соотношениями

; ,

где – тангенциальное ускорение,;

–нормальное ускорение, .

Величина полного ускорения:

.

Углы _nмежду полным и нормальным ускорением и_между полным и тангенциальным ускорением задаются соотношениями

;

.

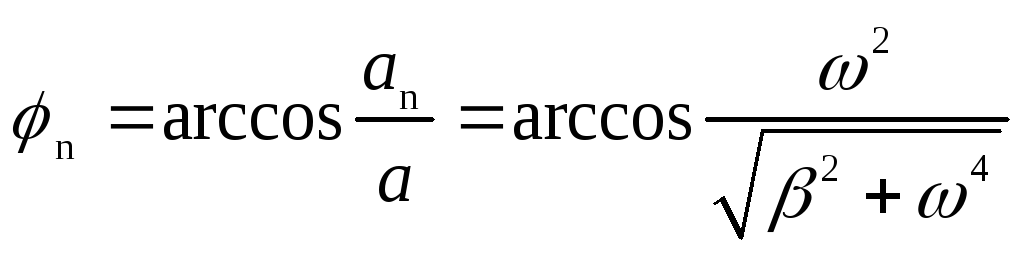Движение абсолютно твёрдого тела представляется как сумма поступательного и вращательного движений. Поступательное движение может быть представлено движением любой точки тела. Чаще всего такой точкой является центр масс. При вращательном движении тела вокруг какой-либо оси все точки тела движутся по окружностям с одинаковыми угловыми скоростями и ускорениями. Основными формулами являются формулы, описывающие движение материальной точки.

Быстрота движения материальной точки по окружности или вращения тела вокруг оси характеризуется частотой вращения n– числом оборотов в единицу времени. Связь величины угловой скоростис частотой вращенияnзадаётся соотношением

Период обращения:

.