Колебания и волны.

Пример 1. Точка совершает гармонические колебания с частотой . В момент, принятый за начальный, точка имела максимальное смещение. Написать уравнение колебаний точки и начертить график.

Решение. Уравнение колебаний точки можно записать в виде

,

где A – амплитуда колебаний;

 – циклическая частота;

t – время;

₀– начальная фаза колебаний.

По определению амплитуда колебаний

.

Циклическая частота связана с частотой n соотношением

.

В момент времени формула принимает вид

,

откуда начальная фаза равна

,

где .

Изменение фазы на 2 не изменяет состояния колебательного движения. Поэтому можно принять

.

С учётом равенств - уравнение колебаний примет вид

,

где ,,.

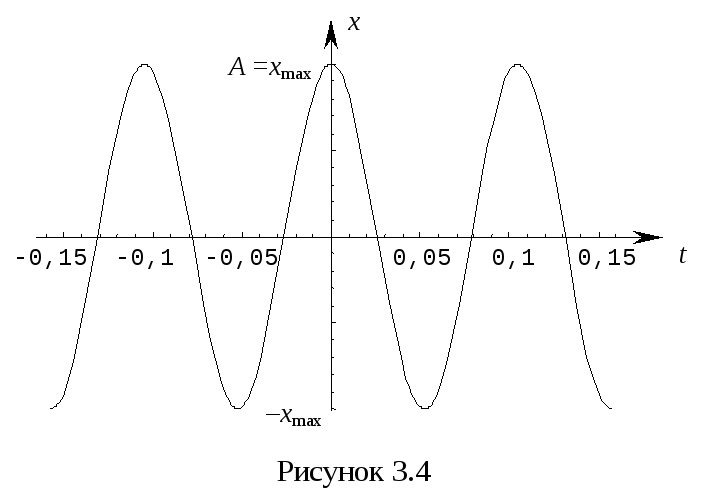
График соответствующего гармонического колебания приведен на рисунке 3.4.

Пример 2. Частица массы совершает гармонические колебания с периодом. Полная энергия колеблющейся частицы. Определить амплитудуA колебаний и наибольшее значение силы F_max, действующей на частицу.

Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы

.

Отсюда амплитуда равна

.

Так как частица совершает гармонические колебания, то сила, действующая на неё, является квазиупругой и, следовательно, может быть выражена соотношением

,

где k – коэффициент квазиупругой силы;

x – смещение колеблющейся точки.

Максимальной сила будет при максимальном смещении x_max, равном амплитуде

.

Коэффициент k выразим через период колебаний:

.

Подставив выражения и в и произведя упрощения, получим

.

Произведём вычисления

;

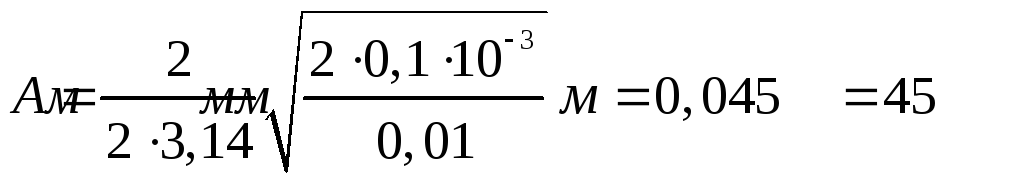Ответ: ;.

Пример 3. Складываются два колебания одинакового направления, выраженные уравнениями

где ;;;;. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Решение. Для построения векторной диаграммы сложения двух колебаний одного направления нужно зафиксировать какой-либо момент времени. Обычно векторную диаграмму строят для момента времени . Преобразовав оба уравнения к канонической форме , увидим, что оба складывающихся гармонических колебания имеют одинаковую циклическую частоту

,

а начальные фазы первого и второго колебаний равны

, .

Произведём вычисления:

;

; .

Изобразим векторы и(рисунок 5). Для этого сложим отрезки длиной и под углами и к оси OX. Результирующее колебание будет происходить с той же частотой и амплитудой , равной геометрической сумме амплитуди:. Согласно теореме косинусов

.

Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (рисунок 3.5).

Произведём вычисления:

;

.

Так как результирующее колебание является гармоническим, имеет ту же частоту, что и слагаемые колебания, то его можно записать в виде

,

где ; ; .

Пример 4. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых

,

,

где ;;;. Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.

Решение. Чтобы определить траекторию точки, исключим время из уравнений и . Заметив, что , применим формулу для косинуса половинного угла

.

Используя это соотношение и отбросив размерности x и y, можно написать

, ,

откуда

.

Э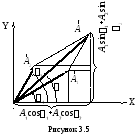то уравнение представляет собой уравнение параболы, ось которой совпадает с осьюOX. Как показывают уравнения и , амплитуда колебаний точки по оси OX равна 1, а по оси OY – 2. Следовательно, абсциссы всех точек траектории заключены в пределах от –1 до +1, а ординаты – от –2 до +2. Для построения траектории найдём по уравнению значения y, соответствующие ряду значений x, удовлетворяющих условию :

x	–1	–0,75	–0,5	0	0,5	1
	0	±0,71	±1	±1,41	±1,73	±2

Н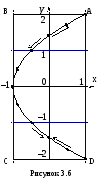ачертив координатные оси и выбрав единицу длины – сантиметр, построим точки. Соединив их плавной кривой получим траекторию результирующего колебания точки. Она представляет собой часть параболы, заключённой внутри прямоугольника амплитудABCD (рисунок 3.6).

Из уравнений и находим, что период колебаний точки по горизонтальной оси , а по вертикальной оси. Следовательно, когда точка совершит одно полное колебание по осиOX, она совершит только половину полного колебания по оси OY. В начальный момент имеем:(точка находится в положенииA). При имеем(точка находится в вершине параболы). Приполучим(точка находится в положенииD). После этого она будет двигаться в обратном направлении.

Пример 5. Тело массы совершает затухающие колебания с циклической частотой. При этом за времятело теряет 0,9 своей полной механической энергии. Найти: а) коэффициент затухания; б) коэффициент сопротивления среды; в) добротность колебательной системы.

Решение. Начальную фазу колебаний можно положить равной нулю, . Тогда уравнение затухающих колебаний имеет решение

,

где коэффициент затухания  связан с коэффициентом сопротивления среды r соотношением

,

а частота затухающих колебаний  связана с частотой свободных колебаний ₀ в отсутствие затуханий соотношением

,

где k – коэффициент упругости затухающей системы.

Полная механическая энергия системы определяется как сумма кинетической и потенциальной энергии

.

Дифференцируя соотношение по времени, найдём скорость затухающих колебаний

.

Подставляя и в и используя соотношение , найдём зависимость полной энергии от времени

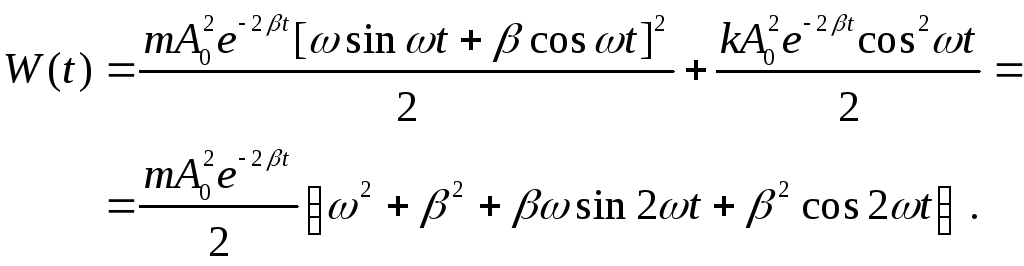
По условию задачи , где. Следовательно, из получаем

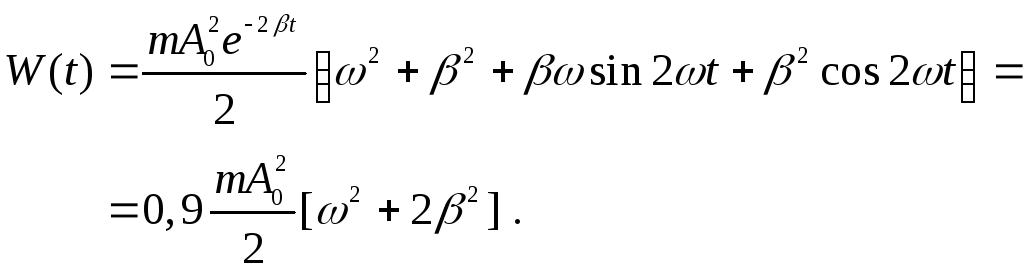
Подставляя сюда численные значения для  и t, заметим, что . Поэтому . Аналогично . Следовательно, из получаем уравнение для определения :

Сокращая на , находим коэффициент затухания

.

Подставляя в , найдём коэффициент сопротивления среды:

.

Добротность вычислим по формуле

.

Полученные значения для коэффициента затухания и добротности свидетельствуют о том, что силы сопротивления среды, действующие в системе, малы и система может достаточно долго колебаться, хотя за первую минуту колебаний она теряет 90% своей энергии.

Ответ: а) :

б) ; в).

Пример 6. Определить амплитуду вынужденных колебаний груза массы на пружине с коэффициентом жёсткости, если на груз действует вертикальная вынуждающая гармоническая сила с амплитудойи частотой, в 2 раза большей собственной частоты груза на пружине. Коэффициент затухания.

Решение. Амплитуду вынужденных колебаний груза следует вычислять по формуле

,

где собственная частота груза на пружине определяется коэффициентом жёскости и массой груза по формуле

.

По условию задачи частота  вынуждающей силы в 2 раза большей собственной частоты груза, т.е.

.

Подставляя и в , находим

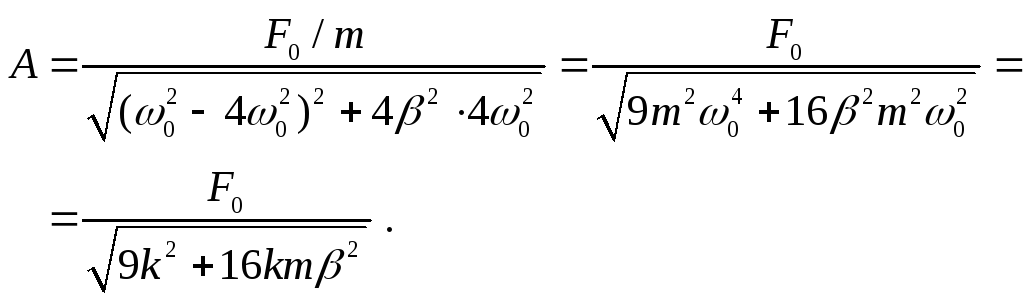
Наконец, подставляя сюда численные значения из условия задачи, получаем

.

Ответ: .

Пример 7. Плоская волна распространяется вдоль прямой со скоростью . Две точки, находящиеся на этой прямой на расстоянияхиот источника волн, колеблется с разностью фаз. Найти: а) длину волны; б) написать уравнение волны; в) смещение указанных точек в момент , если амплитуда.

Решение. Точки, находящиеся друг от друга на расстоянии, равном длине волны , колеблются с разностью фаз, равной

.

Решая это равенство относительно , получаем

.

Подставив числовые значения величин, входящих в выражение , и выполнив арифметические действия, получим

.

Для того, чтобы написать уравнение плоской волны, надо ещё найти циклическую частоту . Так как , где – период колебаний, то

.

Зная амплитуду A колебаний, циклическую частоту  и скорость распространения волны, можно написать уравнение плоской волны для данного случая:

,

где ,,.

Чтобы найти смещение y указанных точек, достаточно в уравнение подставить значения t и x:

,

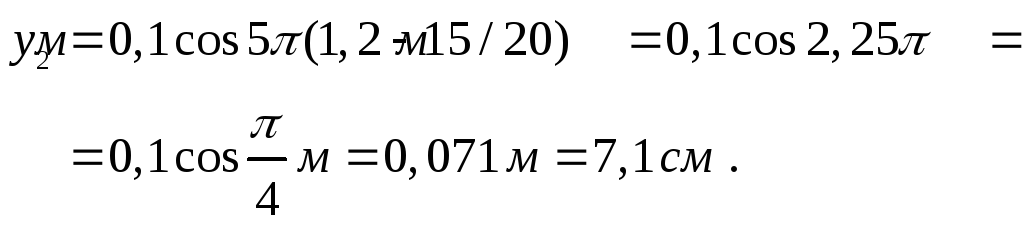
Ответ: а) ; б) ; в) , .