3 Импульсная модуляция

При импульсных видах модуляции в качестве носителя используется, как правило периодическая последовательность прямоугольных импульсов, которая описывается рядом Фурье в следующем виде:

(3.1)

где	– амплитуда импульса,
	– длительность импульса;
	– период следования импульсов.

Учитывая, что угловая частота импульсной последовательности , а отношениеT₁/ =Q– скважность импульсной последовательности, выражение (3.1) представим в виде:

(3.2)

Как следует из выражений (3.1) и (3.2), изменяя модулирующим сообщением амплитуду, длительность импульса, период следования, а также время появления импульсов относительно тактовых точек можно получить соответственно амплитудно-импульсную модуляцию (АИМ), широтно-импульсную модуляцию (ШИМ), частотно-импульсную(ЧИМ) и фазоимпульсную модуляцию (ФИМ).

3.1 Амплитудно-импульсная модуляция

При АИМ амплитуда импульсов изменяется по закону передаваемого (модулирующего) сигнала.

Рассмотрим простейший случай АИМ одним тоном, т.е. когда модулирующий сигнал описывается выражением

(3.3)

a немодулированная последовательность импульсов представляется рядом Фурье (3.2).

Различают АИМ первого (АИМ-1) и второго (АИМ-2) рода. При АИМ-1 высота импульса в пределах его длительности () изменяется по закону модулирующего напряжения. При АИМ-2 высота импульса зависит лишь от значения сигнала в тактовой точке.

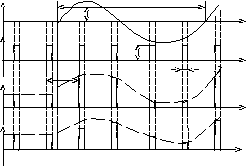
Временные диаграммы АИМ-1 и АИМ-2 сигналов приведены на рисунке 3.1.

C(t) Т

U_

0 t

U(t)

U

0. t

T₁ 

АИМ-1

0 t

АИМ-2

0 t

Рисунок 3.1 – Временные диаграммы АИМ-1 и АИМ-2 сигналов

В соответствии с определением АИМ амплитуда импульсов Uпри АИМ-1 будет изменяться по следующему закону:

(3.4)

где m=kU /U	– коэффициент глубины модуляции,
k	– коэффициент пропорциональности, устанавливающий связь между амплитудой модулирующего сообщения и изменением амплитуды импульсов носителя.

Подставив (3.4) в (3.3), получим выражение для АИМ-1 в виде

(3.5)

Cравнение выражений (3.3) и (3.5) показывает, что в случае модуляции одним тономспектр амплитуд модулированной последовательности импульсов отличается от спектра немодулированной последовательности наличием составляющей с частотой модуляциии боковых составляющих с частотамиkω₁возле каждой гармоники спектра немодулированной последовательнос-ти, представленного на рисунке 3.2.

А_к

Q=3

К_ФНЧ

U

Q

•  2/ 4/

   

ω₁

4ω₁

5ω₁

6ω₁

0

2ω₁

ω

ω₁-

ω₁+

Рисунок 3.2 – Спектр амплитуд АИМ-1 сигнала

Появление в спектре составляющей с частотой можно объяснить следующим образом. Если у последовательности импульсов постоянной высоты среднее значение также постоянно, то у последовательности импульсов, модулированных по амплитуде с частотой(см. рисунок 3.1), и среднее значение изменяется с частотой. Важно заметить, что ширина спектра последовательности импульсов, которую нужно сохранить при передаче, практически не изменяется в результате модуляции по амплитуде (появление боковых частотkω₁не сказывается на ширине спектра). Действительно, в обоих случаях необходимая ширина спектра определяется длительностью импульсов(), которая при АИМ не изменяется:

. (3.6)

На практике в большинстве случаев принимают =1, т.е. необходимая полоса частот определяется первым лепестком спектра, где сконцентрировано около 90энергии всего сигнала. Так как в спектре есть модулирующая частота,то выделить в приемнике первичный сигнал можно фильтром низких частот (см. рисунок 3.2), но для неискаженного выделения необходимо выполнить условие

<ω₁- или ω₁>2. (3.7)

Условие (3.7) соответствует требованиям теоремы Котельникова, рассмотренной ранее.

Если последовательность импульсов модулируется не простым гармоническим сигналом, а сигналом, ширина спектра которого лежит в пределах от _minдо_max, то в спектре модулированного сигнала появляются полосы частот_min_maxиkω₁(_min_max), как показано на рисунке 3.3.

А_к

А₁

Q= 3

А₂

А₀ А₄ А₅

2/

А₆

_min

2ω₁-_min

_max

4/

ω.

2ω₁-_max

Рисунок 3.3 – Спектр амплитуд АИМ-1 сигнала при модуляции

сложным сообщением

Выражение для сигнала АИМ-2 при модуляции одним тоном может быть получена в виде:

(3.8)

Спектр амплитуд АИМ-2 показан на рисунке 3.4.

А_к

Q=3

A_o

•  2/ 4/

 

4ω₁

5ω₁



ω₁

0

3ω₁

ω₁+

ω₁-

2ω₁

ω ω

Рисунок 3.4 – Спектр амплитуд АИМ-2 сигнала

Спектральный состав модулированной последовательности импульсов при АИМ-2 не отличается от спектрального состава при АИМ-1. Несколько изменяются только амплитуды боковых составляющих и составляющих с частотами спектра модулирующего сообщения (3.8).