1.5. Преобразование непрерывных сообщений в дискретные сигналы

1.5.1. Квантование по времени (дискретизация). Непрерывные сообщения представляют собой непрерывные функции времени с бесконечным числом промежуточных точек. Для передачи таких сообщений без погрешности необходим канал связи с бесконечной пропускной способностью. На практике всегда передача сообщений осуществляется с ограниченными спектром частот и точностью, так как все каналы имеют ограниченную пропускную способность.

Если непрерывное сообщение имеет ограниченный спектр частот, оно всегда может быть передано своими значениями в отдельные моменты времени, т.е. может быть превращено в дискретное во времени сообщение, состоящее из последовательного во времени ряда значений.

Возможность такой замены была впервые установлена и сформулирована в 1933 г. В. А. Котельниковым в виде следующей теоремы: «Если функция f(t) не содержит частот выше F_max Гц, то она полностью определяется своими мгновенными значениями в моменты времени, отстоящие друг от друга на 1/2F_max», т. е.

. (1.29)

Функцию с ограниченным спектром можно записать в виде тригонометрического ряда

, (1.30)

где k – порядковый номер отсчета функции.

При этом функция вполне определяется своими мгновенными значениями f(kt), отсчитанными через равные интервалы времени t, называемые интервалами дискретизации (рис. 1.12).

Свойства ряда (1.30) основываются на свойстве функции (sin x)/x, равной 1 при x=0 и равной 0 при x, кратных  (180, 360, 540 и т.д.).

Физический смысл преобразования состоит в том, что каждый член ряда (1.30) представляет собой отклик идеального фильтра нижних частот с граничной частотой среза F_max на очень короткий импульс, возникающий в момент времени kt (рис. 1.12) и имеющий площадь, равную мгновенному значению функции f(t).

Интересным свойством ряда (1.30) является то, что значения ряда в момент kt определяются только k-м членом ряда, так как все другие члены в этот момент времени обращаются в нуль:

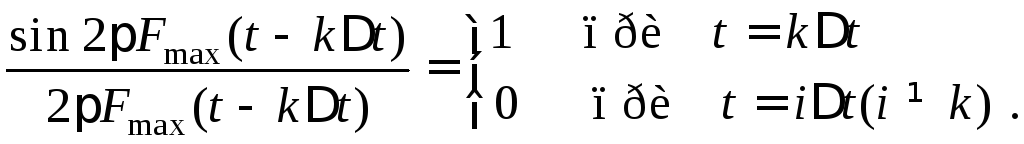(1.31)

Следовательно, несмотря на то, что выходные функции перекрываются, значением заданной функции в момент отсчета является только одно из ее значений.

Согласно теореме Котельникова для однозначного представления функции с ограниченным спектром на интервале времени T достаточно иметь N значений этой функции, т.е.

. (1.32)

Аналогичные результаты можно получить для функций со спектром частот в промежутке от F₁ до F₂.

Таким образом, непрерывное сообщение сводится к сигналу в виде последовательности импульсов, амплитуда которых равна значению исходной функции, передаваемой в дискретные моменты времени kt, а интервалы между ними t = 1/2F_max.

При выполнении условий (1.29) непрерывная и дискретная во времени функции обратимы между собой (тождественны).

Для преобразования дискретной функции в непрерывную нужно включить идеальный фильтр частот с частотой среза равной F_max.

Рассмотренный процесс преобразования непрерывного сообщения в дискретный во времени сигнал называется дискретизацией во времени.

В заключение следует отметить, что при определении на практике интервала дискретизации теорему Котельникова можно применять с поправкой

, (1.33)

где  – коэффициент, зависящий от точности воспроизведения функции и способа интерполяции; при линейной интерполяции , при ступенчатой(относительная погрешность воспроизведения).

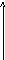
f (t)

t

f (2t)

3t

f (t)

t

2t

t

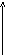
f (3t)

f (0)

f (t)

f (2t)

f (3t)

t

0

sin2πF_max t

f₀ (t)

f(0)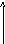

2πF_max t

t

f₁ (t)



sin2πF_max(t-∆t)

)

(

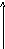
t)

f

2πF_max(t-∆t)

t

2

t)

f



sin2πF_max(t-2∆t)

f₂ (t)

2πF_max(t-2∆t)

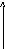
t

f₃ (t)

sin2πF_max(t-3∆t)

f(3 t)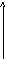



2πF_max(t-3∆t)

t

Рис. 1.12. Разложение функции f(t) с ограниченным спектром

частот по В.А.Котельникову

1.5.2. Дискретизация двумерной функции. Все большую часть передаваемых по линии связи сообщений, составляют сигналы, являющиеся функциями не только времени - λ(t) (речь, музыка и т.п.), но и ряда других переменных, например, λ(x, y), λ(x, y, t) (статические и динамические изображения, карты физических полей и т.п.). В связи с этим естественным является вопрос: можно ли так, как это делается для временных сигналов (или других функций одной переменной), производить дискретизацию многомерных сигналов (функций нескольких переменных)?

Ответ на этот вопрос дает теорема дискретизации для двумерных (или в общем случае – для многомерных) сигналов, которая утверждает: функция двух переменных λ(x, y), двумерное преобразование Фурье которой

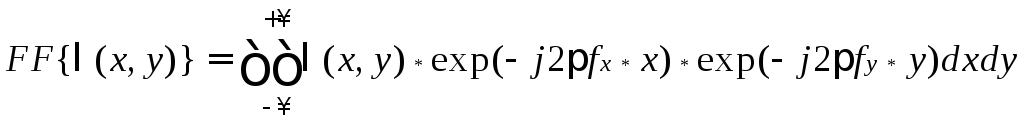(1.34)

равно нулю при f_x ≥ f_x maxиf_y ≥ f_y max, однозначно определяется своими значениями в равноотстоящих точках плоскости переменныхx и y, если интервал дискретизации удовлетворяет условию Δx ≤ 1/2f_xmax, Δy ≤ 1/2f_y. Процедура дискретизации двумерной функции иллюстрируется примером, приведенным на рис. 1.13.

Доказательство двумерной теоремы дискретизации основано, так же как и для одномерного случая, на однозначном соответствии между сигналами и их спектрами: одинаковым изображениям (двумерным функциям) соответствуют одинаковые спектры, и наоборот, если спектры двух функций одинаковы, то и сами эти функции равны друг другу.

Преобразование Фурье (спектр) дискретизованной двумерной функции FF{λ(ix, jy)} получается периодическим продолжением спектра исходной непрерывной функции λ(x, y) в точки частотной плоскости (kf_x , lf_y) (рис. 1.14), где f_x и f_y – так называемые «пространственные частоты», являющиеся аналогами обычной «временной» частоты и отражающие скорость изменения двумерной функции λ (x, y) по соответствующим координатам (крупные фрагменты изображения – низкие частоты, мелкие детали – высокие частоты).

Аналитически это можно записать следующим образом:

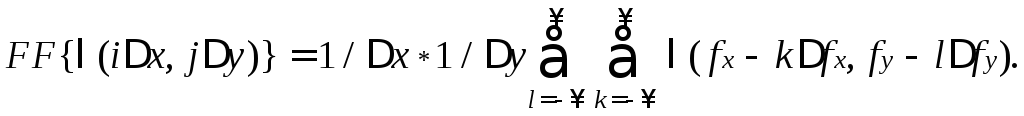(1.35)

Из рис. 1.8 видно, что если соблюдается условие неперекрываемости периодических продолжений спектра FF{λ(ix, jy)},а это справедливо при Δx≤1/2f_xmax , Δy ≤ 1/2f_y max, то с помощью идеального двумерного ФНЧ с частотной характеристикой вида:

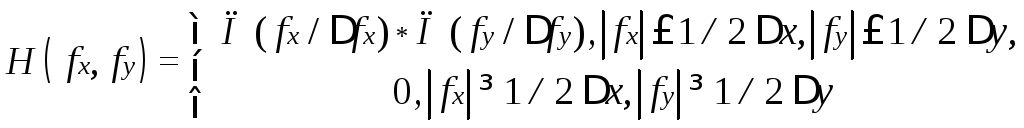(1.36)

из спектра дискретизованной функции FF{λ(ix, jy)} можно абсолютно точно выделить спектр исходной непрерывной функцииFF{λ(x,y)} и, следовательно, восстановить саму функцию.

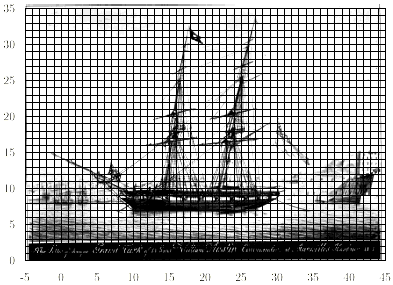
А б

в

Рис. 1.13. Процедура дискретизации двухмерных изображение: а- исходное изображение;б- дискретизация по осямxиy;в– дискретизированное изображение.

Таким образом, видно, что не существует принципиальных отличий в дискретизации между одномерными и двумерными (многомерными) функциями. Результатом дискретизации в обоих случаях является совокупность отсчетов функции, различия могут быть лишь в величине шага дискретизации, числе отсчетов и порядке их следования.

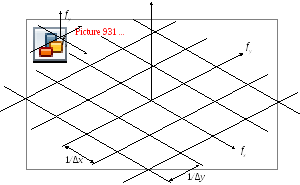
Рис. 1.14 Спектр дискретизированной двухмерной функции.