2.2 Частотная модуляция (чм)

При частотной модуляции по закону модулирующего (передаваемого) сигнала

(2.15)

изменяется мгновенное значение частоты ω₁(t)носителя (рисунок 2.4)

.(2.16)

Мгновенное значение частоты ω₁ модулированного колебания определяется выражением

, (2.17)

где кЧМ	– коэффициент пропорциональности, устанавливающий связь между модулирующим сигналом и изменением частоты носителя;
ω1	– частота немодулированного носителя.

Полная фаза модулированного колебания определяется в виде

. (2.18)

Отсюда видно, что при ЧМ имеет место изменение фазы колебания, т.е. ФМ.

Подставив (2.18) в (2.16), получим выражение для частотно-модулирован-ного сигнала

(2.19)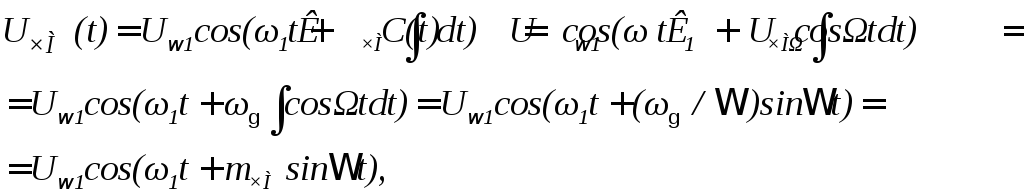

где ωg =кЧМU	– девиация частоты, т.е. максимальное отклонение частоты от значения ω1;
mЧМ= ωg /	– индекс частотной модуляции.

Индекс частотной модуляции фактически равен максимальному отклонению фазы ЧМ-колебания, т.е. m_ЧМ =_max. Он не зависит от средней ω₁ (немодулированной) частоты, а определяется исключительно величиной девиации частоты ω_g и модулирующей частотой .

Векторное представление ЧМ-колебания для рассмотренного случая показано на рисунке 2.5. Вектором U_ω1 показано немодулированное высокочастотное колебание. Чтобы этот вектор был неподвижен, предполагаем, что ось времени вращается по часовой стрелке с угловой скоростью ω₁. Приращение фазы вектора U_ω1 изменяется по гармоническому закону с частотой . Максимальное изменение фазы определяется индексом модуляции m_ЧМ, т.е. вектор U_ω1 отклоняется в обе стороны на угол m_ЧМ. Например, если m_ЧМ =1, то это означает, что вектор U_ω1 отклоняется в обе стороны на один радиан. На практике с целью повышения помехоустойчивости приема при использовании ЧМ применяются большие значения m_ЧМ.

На рисунке 2.6 приведены зависимости индекса модуляции m_ЧМ и девиации частоты ω_g ЧМ-колебания от частоты модулирующего сигнала .

Как видно из рисунка 2.6 и соответствующих выражений, ω_g от  не зависит и определяется только величиной U_, а m_ЧМ с увеличением  убывает.

Рисунок 2.4 – Процесс получения Рисунок 2.6 – Зависимость

частотно –модулированного сигнала m_ЧМ и ω_g от  при ЧМ

2.3 Фазовая модуляция (фм)

При фазовой модуляции по закону модулирующего сигнала изменяется начальная фаза.

Рассмотрим частный случай, когда модулирующий сигнал является гармоническим, т.е.

, (2.20)

а носитель описывается выражением

. (2.21)

Тогда полная фаза ФМ-колебания в соответствии с определением ФМ запишется в виде

. (2.22)

Обозначим

, (2.23)

где mФМ	– индекс фазовой модуляции, т.е. максимальное отклонение фазы колебания;
кФМ	– коэффициент пропорциональности, определяющий связь между модулирующим сигналом и изменением фазы колебания.

Подставив (2.22) в (2.21), получим выражение для ФМ в виде

. (2.24)