
Радіоавтоматика / Lekcija_1_5
.pdfДисципліна: Радіоавтоматика. Лекція 1.5. |
1 |
Лекція 1.5.
Типові ланки автоматики
1.Фізична основа основних ланок автоматики.
2.Підсилювальна ланка.
3.Диференцююча ланка.
4.Інтегруюча ланка.
5.Аперіодична ланка.
6.Ланка затримки.
7.Коливальна ланка.
8.Характеристики реальних ланок автоматики.
1. Фізична основа основних ланок автоматики.
Ланкою системи називається елемент чи його частина, яка має певні властивості.
Фізична основа ланок може бути найрізноманітніша. Вони можуть бути механічними, електричними, гідравлічними, радіозв’язок.
Найпростішими типовими ланками є:
1.Підсилююча ланка (пропорційна);
2.Диференціальна ланка (реальні та ідеальні ланки, форсуючі ланки);
3.Інтегруюча ланка (реальна та ідеальна);
4.Аперіодична ланка (інерційна ланка);
5.Коливальна ланка;
6.Ланка запізнення.
Також можуть бути комбінації вище вказаних ланок.
Дисципліна: Радіоавтоматика. Лекція 1.5. |
2 |
Існують ланки на які діляться складні системи. Розглянемо повні
характеристики кожної елементарної ланки.
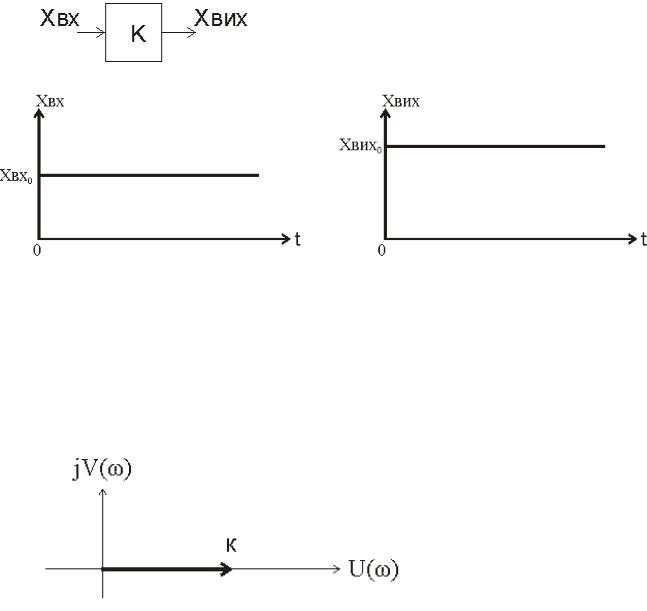
2.Підсилювальна ланка.
Втакій ланці вихідна величина зв’язана з вхідною коефіцієнтом пропорціональності К.
W(p) K
Для ідеальної підсилювальної ланки частотна характеристика відсутня.
Для цього випадку:
W( j ) K
V( ) 0 |
U( ) K → ( ) 0 |
В цьому випадку АФХ має вигляд:
Дисципліна: Радіоавтоматика. Лекція 1.5. |
3 |
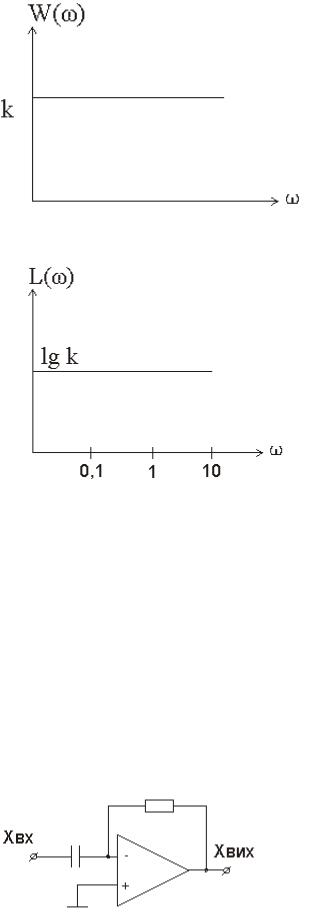
АЧХ має вигляд:
ЛАЧХ:
3. Диференцююча ланка
Ми маємо на увазі спочатку ідеальну. Її рівняння має вигляд:
xвих |
|
dxвх |
K |
p |
d |
|
Xвих xвих |
Xвх xвх |
|
||||||||
|
dt |
|||||||
|
|
dt |
|
|
|
|||
Xвих |
KpXвх |
чи |
Xвих |
рK W(p) |
|
|||
Хвх |
|
|||||||
|
|
|
|
|
|
|
||
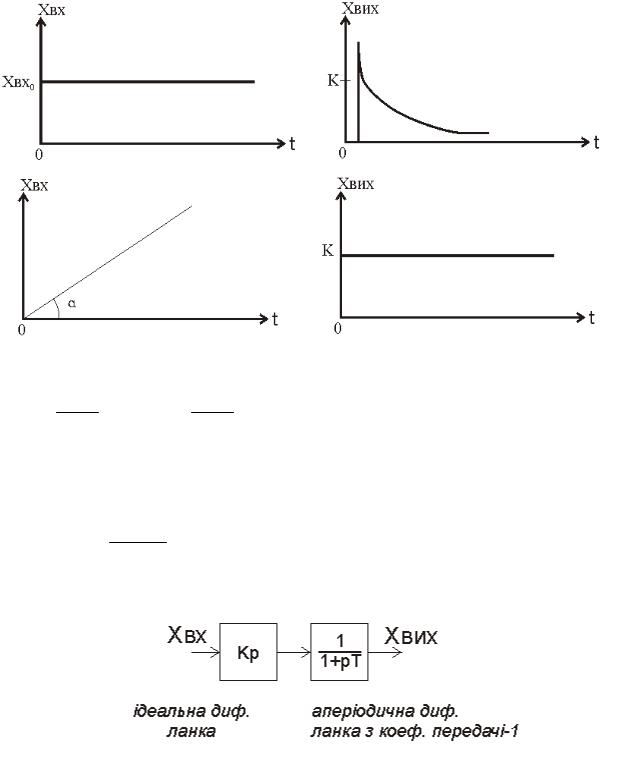
Приклад такої ланки можу бути наступна схема:
Дисципліна: Радіоавтоматика. Лекція 1.5. |
4 |
Якщо K , то можна вважати ідеальною ланкою
p j
W(p) W(j ) j K
Запишемо рівняння для реальної диференціальної ланки:
T dxвих xвих К dхвих
dt dt
Т – постійна диференційної ланки Запишемо передаючу функцію для реальної диференційної ланки:
W(p) Kp
1 pT
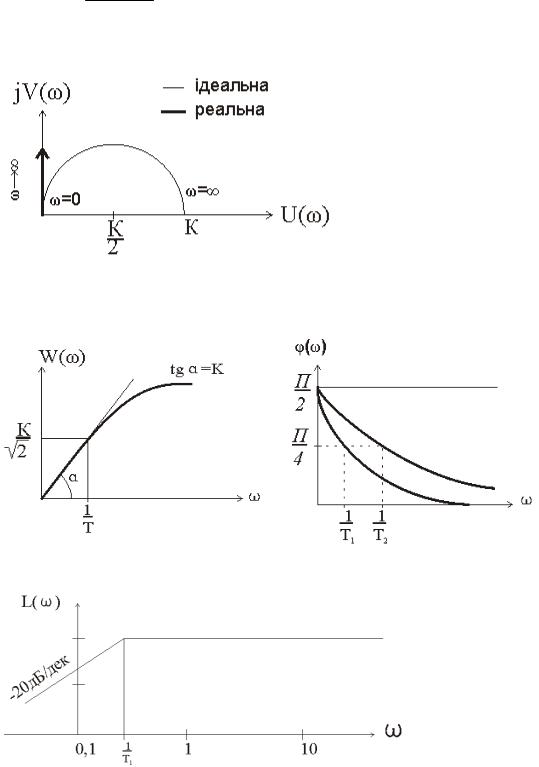
Фактично це означає, що ми маємо справу з двома ланками:
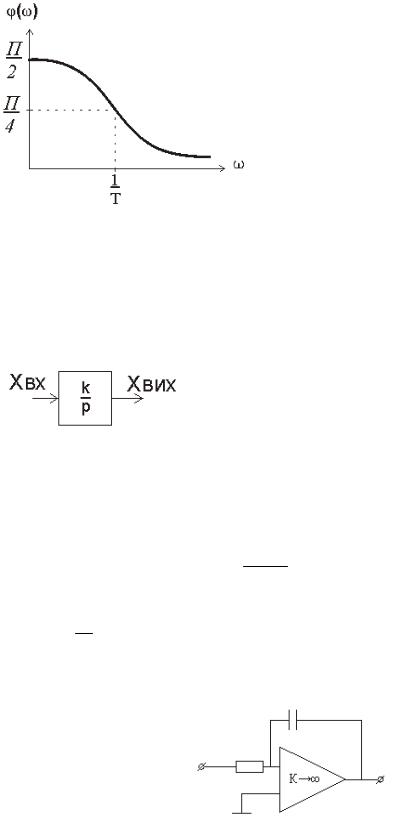
Розглянемо частотні характеристики ідеальної і реальної диференційної ланки:
Дисципліна: Радіоавтоматика. Лекція 1.5. |
5 |
W(j ) j K 1 j T
АФХ:
Якщо K , то отримуємо ідеальну ланку |
|
АЧХ |
ФЧХ: |
Побудували ЛАЧХ
Дисципліна: Радіоавтоматика. Лекція 1.5. |
6 |
ЛФЧХ
4. Інтегруюча ланка.
Спершу розглянемо ідеальну
Рівняння такої ланки виглядає
xвих k xвхdt
dxвих xвхk
dt
k
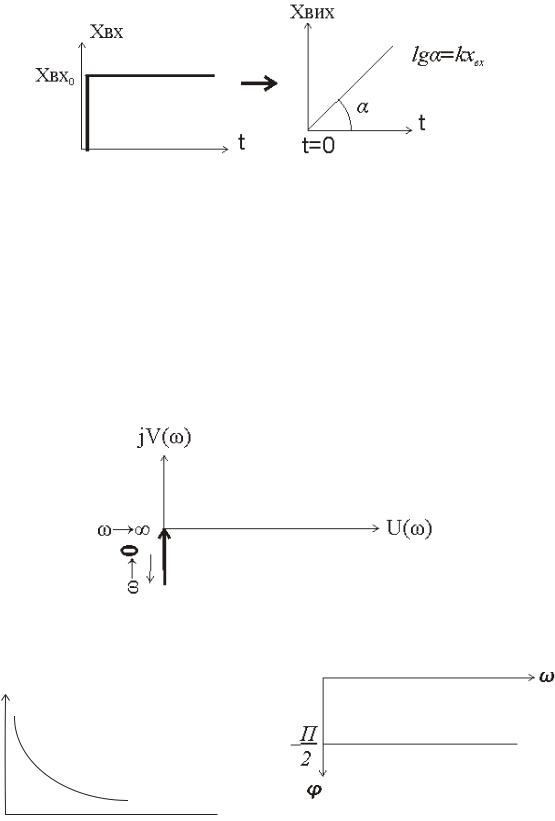
W(p) p – передавальна функція для ідеальної інтегруючої ланки
Прикладом може бути ОП
Розглянемо перехідні характеристики такої ланки
Дисципліна: Радіоавтоматика. Лекція 1.5. |
7 |
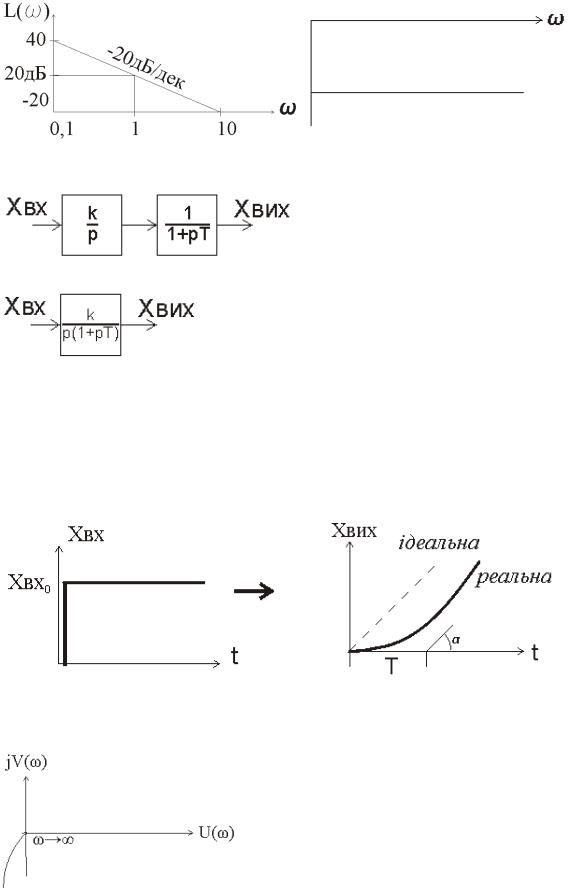
Розглянемо частотні характеристики ідеальної інтегруючої ланки
W( j ) |
k |
j |
k |
|
|
|
|
|||||
|
|
|
|
|||||||||
|
|
j |
|
|
|
|
|
|||||
U( ) 0 |
|
|
|
|
V( ) |
k |
|
|
||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
||
|
|
k |
|
|
j |
|
|
|
|
|||
W( j ) |
|
e |
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
АФХ:
АЧХ |
ФЧХ |
W(ω)
 ω
ω
ЛАЧХ |
ЛФЧХ |
Дисципліна: Радіоавтоматика. Лекція 1.5. |
8 |
Реальну ланку можна подати у вигляді:
Рівняння реальної ланки має вигляд:
T |
d2 |
X |
вих |
|
dX |
вих |
kX |
|
|
|
|
вх |
|||||
dt2 |
|
|
||||||
|
|
dt |
|
|||||
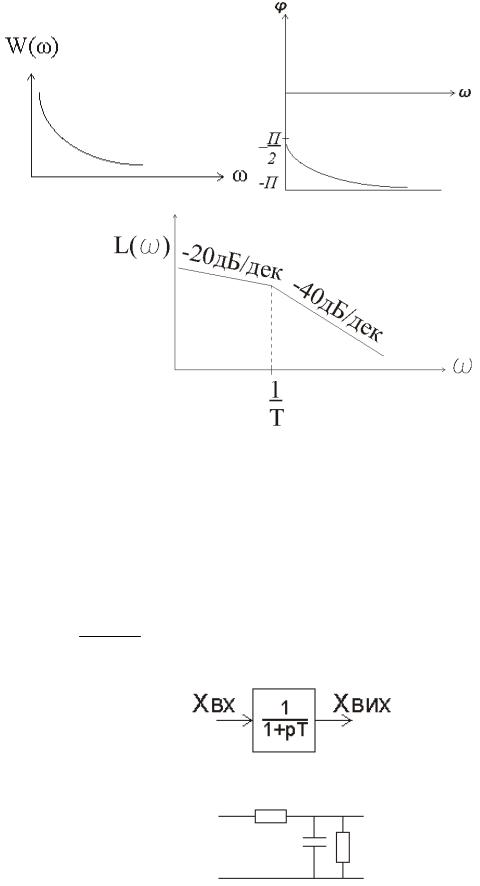
Розглянемо перехідні характеристики реальної ланки:
Частотні характеристики реальної ланки:
АФХ:
АЧХ: ФЧХ:
Дисципліна: Радіоавтоматика. Лекція 1.5. |
9 |
Якщо T→0, то отримаємо ідеальну ланку.
5. Аперіодична ланка.
Передавальна функція має вигляд:
k
W(p) 1 pT – це функція аперіодичної ланки першого порядку
Прикладом може бути:
Перейдемо до комплексного вигляду:
Дисципліна: Радіоавтоматика. Лекція 1.5. |
10 |
k
U( ) 1 2T2 ;
V( )
k T
1 2T2
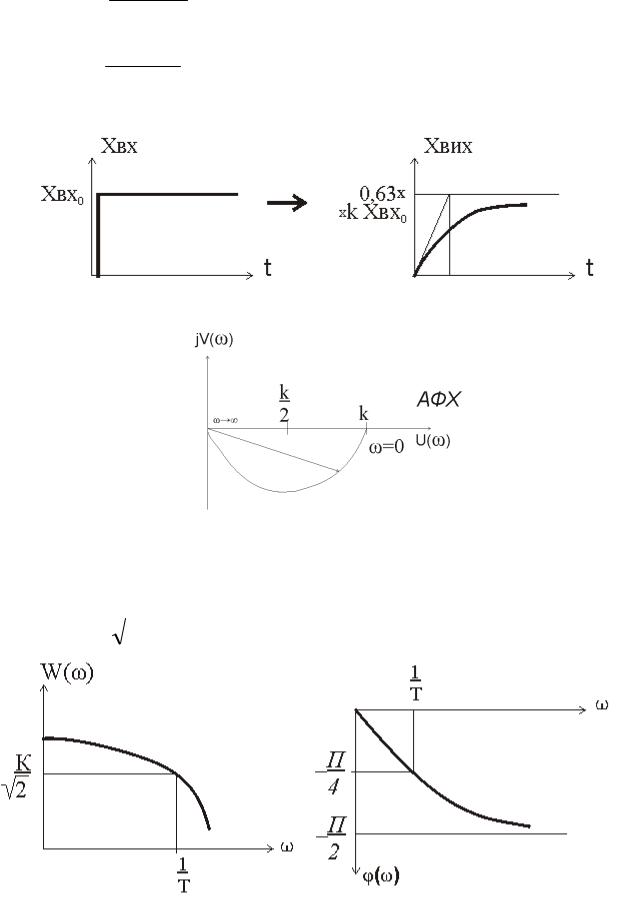
Перехідні характеристики мають вигляд:
Розглянемо частотні характеристики аперіодичної ланки:
Аперіодична ланка І порядку має АФХ, яка лежить в IV квадранті.
АЧХ: ФЧХ:
W( ) |
|
K |
|
( ) arctgT |
|
|
|
|
|||
1 2T2 |
|||||
|
|
|
|||
