
Радіоавтоматика / Lekcija_1_2
.pdf
Дисципліна: Радіоавтоматика. Лекція 1.2. |
1 |
Лекція 1.2.
Перетворення Лапласа.
1.Основи теорії перетворення Лапласа.
2.Передавальна функція.
1. Основи теорії перетворення Лапласа.
Припустимо ми маємо елемент автоматичної системи і на вхід подаємо якусь величину. Нас цікавить який зв'язок існує між вхідною і вихідною діями:
Такий зв'язок може бути заданий диференційним рівнянням,
передавальною функцією, частотною характеристикою:
a |
|
dn Xвх |
|
a |
|
|
dn 1Xвх |
... a |
|
Xвх b |
dm Xвих |
... b Xвих |
|||||||
|
|
dtn |
|
|
|
|
dtn 1 |
|
|
dtm |
|||||||||
|
n |
|
|
|
n 1 |
|
|
|
0 |
m |
0 |
||||||||
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таке рівняння дуже складно розв’язати. В узагальненому випадку це |
|||||||||||||||||||
рівняння можна записати: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
n |
|
di Xвих |
|
m |
|
d j Xвих |
|
|
|
|
|
||||||||
ai |
|
|
|
|
|
bj |
|
|
|
(2) |
|
|
|||||||
|
dt |
i |
|
|
dt |
j |
|
|
|||||||||||
i 0 |
|
|
|
|
|
j 0 |
|
|
|
|
|
|
|
|
|||||
Введемо нові величини Хвих(р) і Хвх(р) і запишемо такі інтеграли:

Дисципліна: Радіоавтоматика. Лекція 1.2. |
|
2 |
||
|
|
|
|
|
Xвих(p) Xвих(t)e pt dt |
|
|
||
|
0 |
|
(3), де р – нова комплексна змінна → јω → d/dt. |
|
|
|
|
||
Xвх(p) Xвх(t)e pt dt |
|
|
||
|
0 |
|
|
|
Такі інтеграли називаються інтегралами Лапласа. |
|
|||
Підставивши (3) в (2) отримаємо: |
|
|||
an pn Xвих an 1 pn 1Xвих ... a0 Xвих |
(4) |
|||
b |
pm Xвх b |
pm 1Xвх ... b Xвх |
||
m |
m 1 |
|
0 |
|
Перехід від (1) до (4) називається перетворенням Лапласа.
L
Якщо ми Xвв(t) X(p) то ми маємо пряме перетворення Лапласа яке
позначається L. А вираз X(p) L 1 Xвв(t) – зворотнє претворення Лапласа, яке позначається L-1.
Запишемо властивості, які слідують із перетворення Лапласа:
1. Операція диференціювання Хвх і Хвих відповідає множенню оригіналу на комплексну частоту:
dx
L dt pX(p)
2. Інтегрування відповідає:
L x(t)dt X(p)
p
3. Перетворення Лапласа від суми оригіналів рівне сумі зображень:
n
L i 1
|
n |
xi (t) |
Xi (p) |
|
i 1 |
4. Константу можна виносити за символ перетворення:
L aX(t) aX(p)
В результаті можна сказати, що в інженерній практиці важко вирішити рівняння (1). Перетворення Лапласа веде до рішення простих алгебраїчних рівнянь.

Дисципліна: Радіоавтоматика. Лекція 1.2. |
3 |
Приклади типових перетворень:
оригінал |
зображення |
|
X(t) |
X(p) |
|
X(t - ) |
e- pX(p) |
|
e t X(t) |
X(p ) |
|
1(t) |
1 |
p |
(t) |
1 |
|
sin |
1 |
(p2 2 ) |
|
|
|

Дисципліна: Радіоавтоматика. Лекція 1.2. |
4 |
2. Передавальна функція
Визначення: завдяки перетворенням Лапласа можна ввести поняття передавальної функції, яка характеризує динамічні властивості системи. З
допомогою динамічної передавальної функції розрахунок АСР спрощується.
Визначимо передавальну функцію:
Xвих |
b pm b |
m 1 |
pm 1 |
... b |
|
Q(p) |
|
|
|
m |
|
0 |
|
|
|
|
an pn an 1 pn 1 |
... a0 |
|
||||
Хвх |
|
P(p) |
|||||
Xвих(р)
W(p) Хвх(р) (7) це відношення визначає передавальну функцію і
звідси очевидно, що:
Хвих(р) W(p)Xвх(p)
Часто ставиться завдання визначити вид передавальної функції. Це завдання аналізу.
Приклад: Визначити передавальну функцію даної ланки:
1) |
W(p) |
Xвих(р) |
|
U2 |
|
|
R2 |
R R |
|
|
1 |
|
|
|
R R |
|
|
||||||||
|
Хвх(р) U |
1 |
|
1 |
2 |
2 |
||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
W(p) 1 k 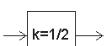
2
Визначити передавальну функцію ланок:
2)

Дисципліна: Радіоавтоматика. Лекція 1.2. |
5 |
1 |
|
|
|
Z1 |
|
|
|
1 |
|
|
|
1 |
||
W(p) |
|
|
|
|
c |
|
|
|
||||||
W(p) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
Z |
|
Z |
|
|
|
|
1 |
|
1 Rc |
||||
1 RC |
|
|
|
|
R |
|
|
|
||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
T |
c |
|
|
|
|
|
W(p) |
1 |
|
|
|
|
||
1 pT |
|
||
3) Знайти самостійно:
