
Радіоавтоматика / Lekcija_1_3
.pdf
Дисципліна: Радіоавтоматика. Лекція 1.3. |
1 |
Лекція 1.3.
Часові характеристики автоматичної системи.
Перехідні та імпульсні характеристики.
1.Часові характеристики автоматичної системи.
2.Імпульсна характеристика ланки чи системи.
3.Статичні властивості ланок і систем.
4.Частотні характеристики ланок і систем.
1. Часові характеристики автоматичної системи.
До типових впливів відносяться ступінчата та імпульсна дія
f1 1(t) |
f3 e t |
f2 (t)
f4 sin t
Можна розв’язати диференційне рівняння яке описує перехідний процес з даного стану в інший. Краще якщо цей процес представити графічно.

Дисципліна: Радіоавтоматика. Лекція 1.3. |
2 |
Якщо маємо графічний вигляд такої залежності, то ми маємо тимчасові
характеристики ланки:
1.для впливу 1(t) графік k0 зображення є перехідною характеристикою. А аналітичні залежності – перехідна функція.
2.при впливі δ(t) графік зображення вихідної величини називається імпульсною характеристикою, а аналітичний вигляд називається імпульсною перехідною функцією (ваговою функцією).
В АСР ступінчатий вплив використовується частіше, так як тут яскраво проявляються динамічні властивості об’єкту при переході із одного стану в інший. Будь-який складний вплив можна звести в ряд простих впливів.
Xвх(t) x0 x(t t) x2 (t t) ...
X0вх 1
Xвих h(t) – перехідна характеристика для одиничного впливу.
(1) Xвх(p) Xвх 1(t) 1
p
(2) Xвих(p) h(t) h(p)
Перехід від h(t) (p)відбувається через перетворення Лапласа.
Xвих(p) h(p)
(3) W(p) Xвх(p) 1 ph(p)
p
Дисципліна: Радіоавтоматика. Лекція 1.3. |
3 |
Якщо ми знаємо перехідну функцію системи, то зможемо знайти
передавальну функцію.
(3`) – h(p) 1 W(p) p
(4)h(t) 1 W(p)/ p .
2.Імпульсна характеристика ланки чи системи
Імпульсна характеристика частіше використовується в радіоавтоматиці.
Імпульсна характеристика може визначатися через зворотнє перетворення Лапласа.
g(p) W(p) |
|
|
|
||
L 1 W(p) L 1 g(p) g(t) |
(5) |
|
|||
h(t) L 1 W(p)/ p ; |
|
g(t) L 1 W(p) ; |
(5`) |
||
g(t) p h(t) |
d |
h(t) |
– зв'язок між імпульсною |
та перехідною |
|
|
|||||
|
dt |
|
|
|
|
характеристиками.
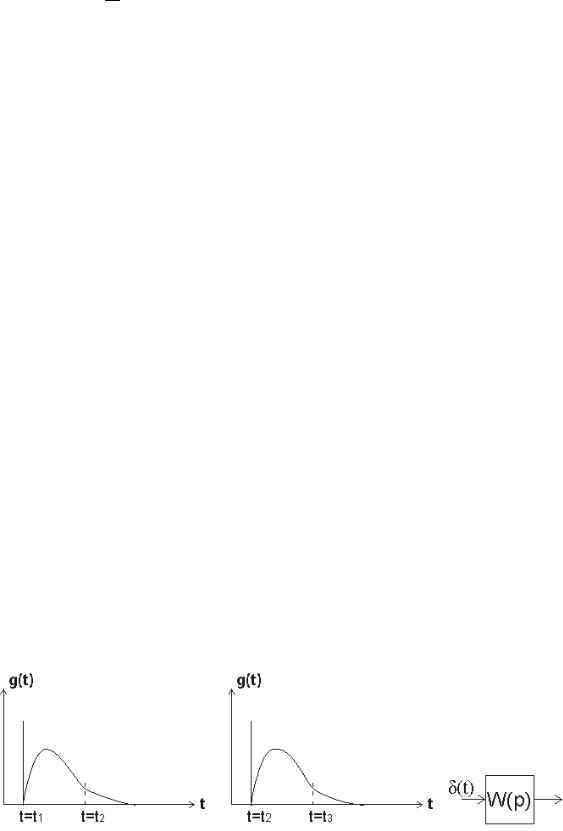
Якщо існує інтервал часу, де g(t)≠0, то така система володіє пам’яттю,
тобто існує відгук системи на імпульсний вплив.
Для радіосистем такий відгук залежить від властивості системи. Якщо ланка автоматики стаціонарна, то відгук визначається лише часом спостереження та відліку від дії Δt.
1) cтаціонарна система.

Дисципліна: Радіоавтоматика. Лекція 1.3. |
4 |
У нестаціонарної системи характеристики змінюються на протязі часу.
Для нестаціонарних систем форма імпульсної характеристики залежить від часу дії одиничного імпульсу: δ(t).
Знання передавальної функції об’єкту в повній мірі відображає динамічні властивості такого об’єкту.
Якщо нам відомі h(t) і g(t) (експериментальні криві) то можна знайти вигляд передавальної функції W(t).
3. Статичні властивості ланок і систем
До характеристик ланок відносяться статичні та динамічні характеристики.
Визначення: статичні характеристики визначають залежність між вхідною і вихідною величиною установленого стану.
Визначення: динамічні характеристики визначають властивості системи і ланки в перехідному режимі, тобто з одного рівноважного стану в інший.
Динамічні характеристики поділяються на тимчасові, перехідні і частотні.
В більшості випадків статичні характеристики нелінійні. Залежність такої характеристики може бути виражена графічно чи аналітично.
Подивимось які залежності статична характеристика може приймати:

Дисципліна: Радіоавтоматика. Лекція 1.3. |
5 |
1. паралельне з’єднання ланок:
Статична сумарна характеристика знаходиться простим складанням координат
2. послідовне з'єднання ланок статичної характеристики:

Дисципліна: Радіоавтоматика. Лекція 1.3. |
6 |
Характеристики такі ж
3. зустрічно-паралельне з'єднання ланок:
W1(р`) – загальна, передавальна функція для вище намальованої системи
при ВОЗ.
W2(р) – передавальна функція системи при ДОЗ.
Якщо ланка має статичну характеристику, то ланка є статичною.
Якщо ланка не має статичної характеристики, то ця ланка називається астатичною.

Дисципліна: Радіоавтоматика. Лекція 1.3. |
7 |
Приклад статичної ланки – електродвигун постійного струму.
Якщо для статичних ланок перша похідна вихідної величини рівна const,
то ця статична ланка першого порядку. Якщо друга похідна =const, то це статична ланка другого порядку.
Ознака астатизму – наявність комплексної перемінної р в знаменнику передавальної функції W(р).
W(p) Хвих(р) |
Wc(p) |
|||
|
Хвх(р) |
|
p |
Якщо γ=0, то система статична |
Якщо γ=1, то маємо астатичну систему.
Статичні ланки – підсилююча ланка, аперіодична ланка, диференційна ланка, коливальна ланка, ланка запізнення.
Астатична ланка – це інтегруюча ланка. Об’єднуючи дві інтегруючі ланки підряд ми отримаємо астатичну ланку другого порядку.
4. Частотні характеристики ланок і систем
Визначення:
Xвх(р) |
р j |
Xвих(р)
Передавальна функція:
W(p) Xвих(р)
Хвх(р)
При подачі на вхід якогось чотирьохполюсника ω то на виході отримуємо ту саму частоту, але змінюється амплітуда і фаза сигналу.

Дисципліна: Радіоавтоматика. Лекція 1.3. |
8 |
Xвх(t) Aвх sin t
Xвих(t) Aвих sin( t )
U1 Aвх cos t
Vp Aвх sin t
X |
вх |
А (cos t jsin t) |
|
вх |
|
|
|
ej t |
Xвих Аивх(cos( t ) jsin( t ))
ej t cos t jsin t (формула Ейлера)
Xвх Авхej t
Xвих Авихej( t )

Дисципліна: Радіоавтоматика. Лекція 1.3. |
|
9 |
|||||||||
|
|
|
|
|
вих (t) |
|
Авих |
ej( db[ вх ) |
|
|
|
|
|
Х |
W( j ) |
(АФХ) |
(*) |
||||||
|
|
|
|
|
|
|
|||||
|
|
|
Х вх (t) |
Авх |
|
||||||
|
|
|
|
|
|
||||||
Ми отримали амплітудно фазову характеристику системи. Вона формально схожа на передавальну функцію.
Відношення модулів вихідної величини і вхідної дає модуль АФХ, тобто
Авих модуль_ АФХ W( )
Авх
Визначимо ФЧХ
вих вх фаза_ АФХ ( ) ФЧХ
формулу (*) можна переписати більш класично:
W( j ) W( )ej ( )
АФХ |W( j )| W( )ej ( )
W( )
kp
W(p) 1 pT – реальна диференціальна ланка
W(p) kp– ідеальна диференціальна ланка.
Так отримаємо АФХ для даної реальної диференціальної ланки.
W( j ) |
j k |
АФХ |
|
1 j T |
|||
|
|
ФЧХ ми визначаємо як відношення амплітуд вхідної і вихідної величини ФЧХ визначаємо як різницю фаз.
Якщо розділити справжню (дійсну) і уявну частини, то АФХ запишеться в такому вигляді:
W( j ) U( ) jV( )
|W( j )| W( ) 
 U2 ( ) V 2 ( )
U2 ( ) V 2 ( )
Фаза записується у вигляді:

Дисципліна: Радіоавтоматика. Лекція 1.3. |
10 |
( ) arctg V( )
U( )
1.Амплітудно-фазова характеристика – АФХ – W(jω)
2.Амплітудно-частотна характеристика – АЧХ – W(ω)=|W(jω)|
3.Фазо-частотна характеристика – ФЧХ – φ(ω)=arctgV(ω)/U(ω)
4.Дійсна частотна характеристика U(ω)
5.Уявна частотна характеристика V(ω)
U(ω) – парна функція частоти, тобто U(ω)= U(-ω)
V(ω) – непарна функція частоти, тобто V(ω)=-V(-ω)
Приклад: побудова АФХ по вигляду передавальної функції
W(p) |
|
k |
|
; |
|
|
p j |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
1 pT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
W( j ) |
|
k |
|
|
|
1 j T |
j |
|
Tk |
|
|
k |
|||||
|
|
|
|
|
|
|
2 |
|
2 |
2 2 |
|||||||
|
1 j T 1 j T |
|
1 T |
|
|
1 T |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
U |
|
W( j ) jV U |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ω |
|
|
|
V |
|
|
U |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
k |
|
|
|
|
|||
1 |
|
|
|
|
Tk |
|
|
k |
|
|
|
|
|
|
|||
|
|
|
|
|
1 T2 |
|
|
1 T2 |
|
|
|
||||||
… |
|
|
|
… |
|
|
… |
|
|
|
|
||||||
∞ |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|||||
Розглянемо 2-ий метод побудови годографа
