
Радіоавтоматика / Lekcija_2_1
.pdf
Дисципліна: Радіоавтоматика. Лекція 2.1. |
1 |
Лекція 2.1.
Частотні характеристики з’єднань та їх систем
1.Постановка задачі визначення основних характеристик типових ланок.
2.Замкнуті системи.
3.Частотні характеристики замкнених систем.
4.Типові передавальні функції автоматичних регуляторів.
1.Постановка задачі визначення основних характеристик типових ланок.
Задача полягає в тому: як визначити характеристики коли типові ланки
зв’язані в систему.
W( j ) W1( ) W2( )...Wn ( )ej[ 1( ) 2 ( ) ... n ( )]
W( j ) W( )ej ( )
W( ) W1( ) W2( )...Wn( )
( ) 1( ) 2( ) ... n( )
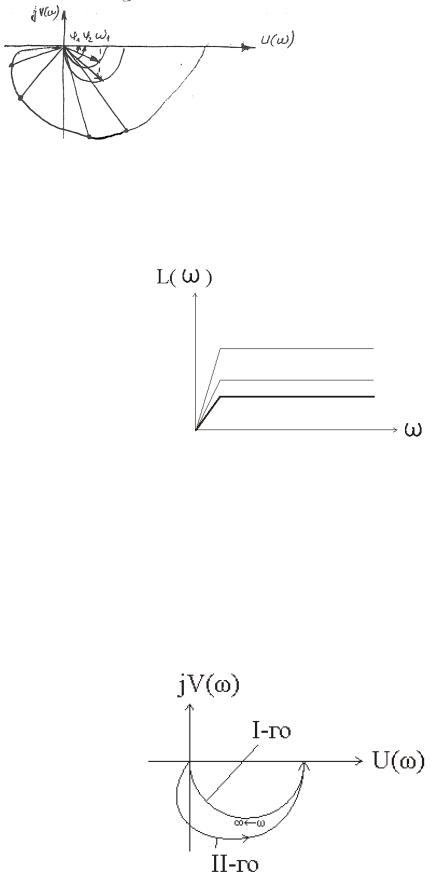
Намалюємо результуючий годограф для систем двох ланок.
Дисципліна: Радіоавтоматика. Лекція 2.1. |
2 |
K K1 K2 1 2
Якщо ми розглянемо логарифмічну характеристику, то в цьому випадку ми отримаємо годограф з допомогою додавання, тобто
n
L( ) Li ( )
i 1
n
( ) i ( )
i1
Вигляд годографа сильно залежить від астатизму системи.
Астатизм системи визначається наявністю інтегруючої ланки
Годографи аперіодичних ланок І і ІІ порядків.

Дисципліна: Радіоавтоматика. Лекція 2.1. |
3 |
Якщо до аперіодичної ланки додати інтегруючу ланку отримаємо годограф виду:
Якщо ми до цієї системи додамо ще одну інтегруючу ланку, то отримаємо годограф виду:
2. Замкнуті системи.
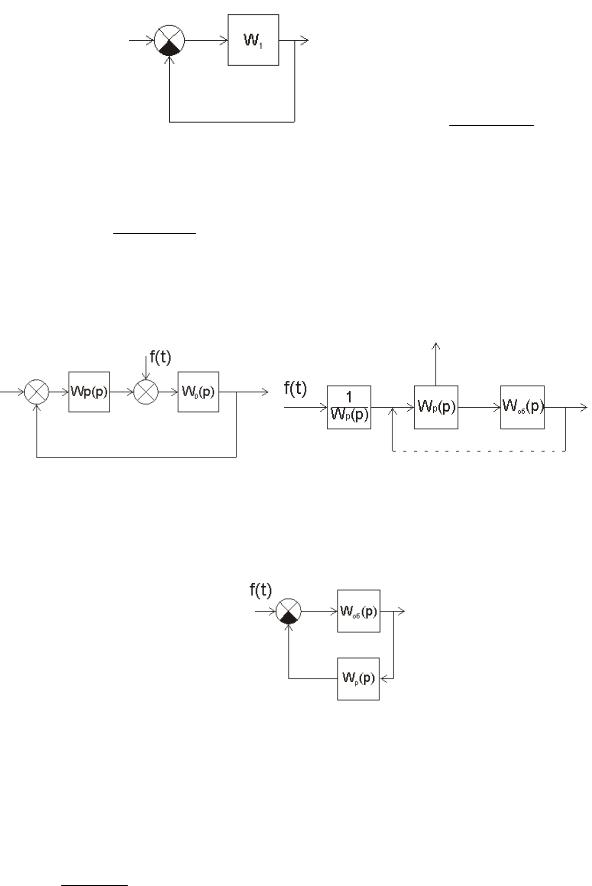
Замалюємо схему паралельно зустрічно ввімкнених ланок:
W(p) W1(p) 1 W1(p) W2(p)
Дисципліна: Радіоавтоматика. Лекція 2.1. |
4 |
W(p) W1(p) 1 W1(p)
Такі замкнуті системи з ОЗ виражаються:
Ф(p) W(p) 1 W(p)
Для таких точок потрібно прикласти в точку і відносно цієї точки потрібно будувати і аналізувати систему.
W(p) |
1 |
|
W(p)1 |
|
Wоб (p) |
|
|
1 Wp (p) jWоб (p) |
|||
|
W1(p) 1 Wp (p) Wоб (p) |
|
|||
Цей запис описує систему наступного вигляду:
3. Частотні характеристики замкнених систем.
Якщо ми маємо передавальну функцію замкненої системи
W(p)
Ф(p) 1 W(p) , тобто є ланка:

Дисципліна: Радіоавтоматика. Лекція 2.1. |
5 |
де W(р) – передавальна функція системи в розімкненому стані. Тоді
систему можна записати і в замкненому стані:
Ф( j ) W( j )
1W( j )
Ф( j ) Ф( )еj ф ( )
Ф( ) – АЧХ замкненої системи
ф( ) – зсув фаз для замкненої системи
Ф( j ) Uф( ) jVф( )
Lф( ) 20lgФ( )
W(p)
Ф( )
1 W(p)
( ) arctg Vф( )
Uф( )
Висновки:
1.Із АФХ замкненої системи можуть бути отримані всі частотні характеристики, при умові якщо заданий вид.
2.Частотні характеристики можна отримати із частотних характеристик розімкненої системи.
Приклад: визначення АЧХ замкненої системи по АФХ розімкненої
системи.
Для розімкненої системи маємо годограф:

Дисципліна: Радіоавтоматика. Лекція 2.1. |
6 |
ВА ОА ВО
Ф( ) |
|
|
|
W(p) |
1 |
– АЧХ для розімкненої системи. |
||
|
|
|
|
|
|
|
||
|
|
1 W(p) |
|
|
||||
|
|
|||||||
|
|
|
|
|||||
|
|
|
|
|
1 |
|
||
4. Типові передавальні функції автоматичних регуляторів.
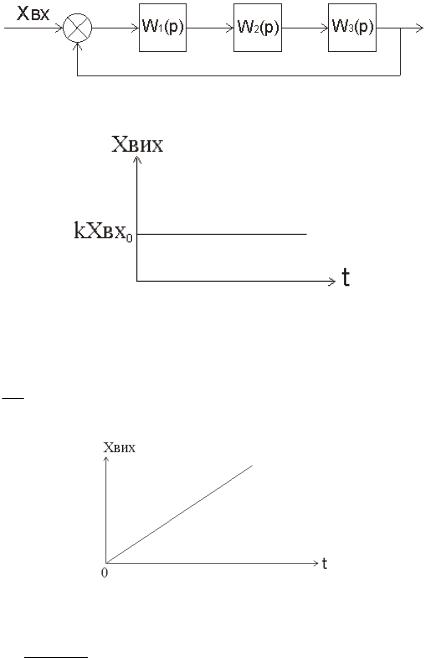
Мал.1
Намалюємо практичну схему автоматичного регулювання (мал. 1), де
Wр(р) – об’єкт регулювання.
Дисципліна: Радіоавтоматика. Лекція 2.1. |
7 |
Існують такі типи законів регулювання:
1.пропорційний;
2.диференціальний;
3.інтегральний, а також їх комбінації.
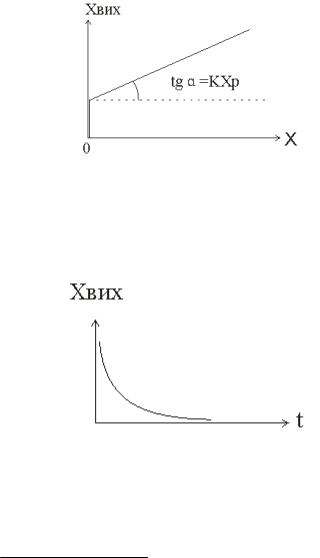
1)Пропорційний закон регулювання можна забезпечити з допомогою включення між ланками підсилюючої ланки:
W(p) K
Мал. 2
2) Для інтегрального закону регулювання замість ланки W3(p) на мал. 2
потрібно покласти інтегральну ланку.
W(p) K p
3) Закон регулювання пропорційної та інтегральної ланки:
W(p) K Tu p 1
Tu p
Дисципліна: Радіоавтоматика. Лекція 2.1. |
8 |
4) Диференціальний закон регулювання забезпечує при заміні ланки
W3(p) диференціальною ланкою:
W(p) K p
5)Запишемо закон регулювання для пропорційно-інтегрально-
диференціальної (ПІД) ланки:
W(p) K TgTu p2 Tu p 1
Tu p
