Радіоавтоматика / Lekcija_2_2
.pdf
Дисципліна: Радіоавтоматика. Лекція 2.2. |
1 |
Лекція 2.2.
Критерії стійкості автоматичних систем
регулювання
1.Основні Критерії стійкості АСР.
2.Логарифмічний критерій стійкості.
3.Стійкість системи з запізненням.
4.Критерій стійкості Михайлова.
5.Критерій стійкості Найквіста.
1.Основні критерії стійкості АСР.
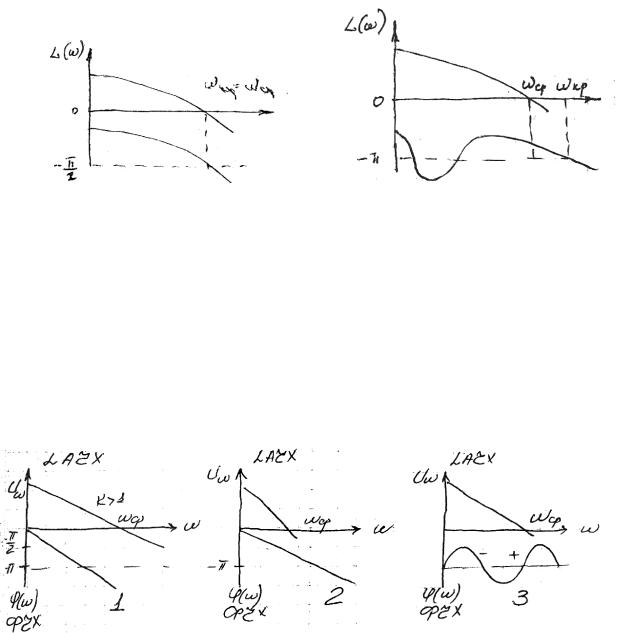
Логарифмічний критерій визначення стійкості
Дисципліна: Радіоавтоматика. Лекція 2.2. |
2 |
Для стійкості в замкненому стані необхідно, щоб виконувалась умова:
кр ср
2. Логарифмічний критерій стійкості.
Ми розглянули такі характеристики:
1.Система нестійка так як К>1;
2.Система нестійка так як К>1;
3.Система умовно стійка.
Визначення:
Запас стійкості по амплітуді показує на яку величину повинен змінитись модуль розімкненої системи на частоті при якій фазова характеристика досягає значення (-) П для того, щоб замкнена система здавалась на границі стійкості.
Запас стійкості по фазі показу на яку величину повинно збільшитись відставання по фазі розімкненої системи на частоті К=1.
Дисципліна: Радіоавтоматика. Лекція 2.2. |
3 |
Запас стійкості АР 6 120 |
30 |
. |
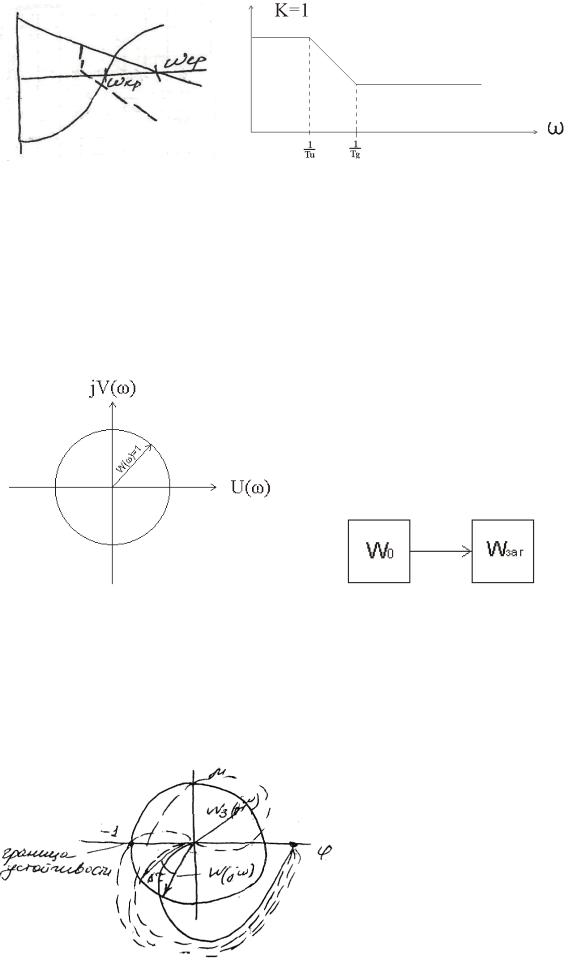
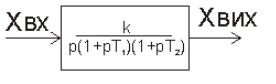Розглянемо приклад: запишемо ланку методом ЛАЧХ. Якщо відомо К=50с-1 Т1=0,04 с система в замкненому стані.
Намалюємо годограф цієї системи:
Знайдемо критичні частоти:
|
|
1 |
25c 1 |
|
|||
1кр |
|
T |
|
|
|
1 |
|
Дисципліна: Радіоавтоматика. Лекція 2.2. |
4 |
|
2кр |
|
1 |
100c 1 |
|
||||
|
|
T |
||
|
|
|
2 |
|
Щоб визначити нахил і прив’язатись до масштабу знаходимо
L1 20lgK 20lg50 34дБ
Відповідно:
– 20 об./дек.
– 40 об./дек. додаються
–60 об./дек.
( ) 90 arctgT1 arctgT2
Запас: |
20 |
8об |
|
|
|
|||
В цьому секторі діє К/р |
|
|
|
|
|
|||
Складаємо таблиці: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ω |
0,1 |
|
1 |
10 |
|
60 |
100 |
1000 |
|
|
|
|
|
|
|
|
|
φ(ω) |
-90° |
|
-93° |
-118° |
|
-180° |
-211° |
-263 |
|
|
|
|
|
|
|
|
|
Розглянемо нестійку систему: щоб система була стійкою потрібно
додати ось таку ланку з характеристикою:
Дисципліна: Радіоавтоматика. Лекція 2.2. |
5 |
3. Стійкість системи з запізненням.
При наявності в системі запізнення в розімкненій системі характер зміни перехідних процесів не змінюється, а лише зсувається на час запізнення τ.
Запишемо годограф для ланки запізнення:
Передавальна функція запишеться для Wз (p) e p
Сумарна передавальна функція: Wз (p) W0e p
Годограф такої системи:
Дисципліна: Радіоавтоматика. Лекція 2.2. |
6 |
W( j ) W ( )ej[ ( ) ] |
(1) |
|
|
0 |
|
W ( j ) W ( )ej ( ) |
|
|
0 |
0 |
|
Змінимо час запізнення τ:
1) якщо збільшимо τ, то буде змінюватись лише кут, модуль не буде змінюватись у формулі (1). Із малюнка вино, що чим більше збільшувати τ,
то система буде стійкою і нестійкою. Тобто така система залежить від τ.
4. Критерій стійкості Михайлова.
Це графічний критерій. Його запропоновано у 1938 році радянським вченим А.В. Михайловим, він також базується на розгляді полінома D( ).
Рис. 13-1. До критерію стійкості А.В. Михайлова
Підставимо у цей поліном замість уявну змінну j . В результаті отримаємо комплексну функцію
D(j )=UD ( )+ jVD ( ).
Дисципліна: Радіоавтоматика. Лекція 2.2. |
7 |
Тут UD ( ) - дійсна частина, отримана з членів D( ), що містять парні степені
, а VD ( ) - уявна частина, отримана з членів D( ) з непарними степенями .
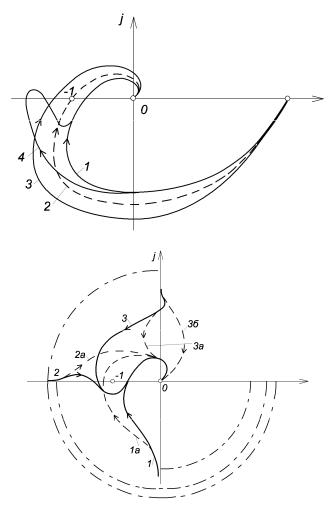
Зобразимо D(j ) у вигляді годографа у комплексній площині (крива 1
на рис. 13-1, а). Цей годограф називається годографом Михайлова. Кожному
значенню відповідають певні значення UD ( ) і VD ( ) й певна точка на площині. При = 0 функція D(j )= an , тобто годограф починається на дійсній осі. При → ∞ функція D(j ) також необмежено зростає.
Критерій Михайлова формулюється так: система є стійкою, якщо годограф D(j ) , починаючись на дійсній додатній півосі, огинає проти годинникової стрілки початок координат, проходячи послідовно n
квадрантів, де n порядок системи. Доведення критерію див у роботах [3, 11, 33].
На рис. 13-1, а годограф 1 відноситься до стійкої, а годографи 3, 4 й 5
до нестійких систем.
Умовою знаходження системи на границі стійкості є проходження голографа Михайлова через початок координат (штрихова крива 2 на рис. 13- 1, а). Дійсно, у цьому випадку існує значення , при якому D(j )= 0. Тобто,
характеристичне рівняння системи має пару спряжених уявних коренів
= ± j . Останнє саме і означає наявність в системі незатухаючих коливань,
тобто знаходження її на границі стійкості. Незначна зміна параметрів системи, у результаті чого годограф на рис. 13-1, а відійде вліво або вниз від початку координат, робить систему стійкою, а зміна параметрів у протилежний бік нестійкою.
На рис. 4-3, б наведено годографи стійких систем різних порядків до
n = 6.
При практичній побудові годографа D(j ) перш за усе знаходять точки його перетину із координатними осями. Для цього, визначаючи з рівняння
UD ( ) = 0
Дисципліна: Радіоавтоматика. Лекція 2.2. |
8 |
значення частот, що відповідають точкам перетину годографа D(j ) з уявною віссю, підставляють їх у вираз VD ( ) . В результаті отримують відповідні ординати. Аналогічно знаходять точки перетину D(j ) з дійсною віссю,
прирівнюючи нулю уявну частину VD ( ) й підставляючи потім знайдені при цьому значення у вираз для UD ( ).
Власне, після знаходження значень , при яких годограф перетинає осі координат, тобто знайдено нулі UD ( ) й VD ( ), для висновку щодо стійкості системи вже немає необхідності будувати сам годограф. З
формулювання критерію Михайлова випливає, що стійкість має місце, якщо та VD ( ) чергуються із зростанням , починаючи з = 0 , коли
UD ( ) > 0.
Щоб не мати справу з високими степенями , побудову годографа
D(j ) можна виконувати по ланках системи. Представимо D(j ) таким чином:
D(j )= R(j )+Q(j )= ∏Ri |
(j )+∏Qi (j ), |
(13-1) |
i |
i |
|
де Ri (j ) і Qi (j ) чисельник та знаменник амплітудно-фазової частотної характеристики i-ї ланки приведеної одноконтурної системи.
Згідно виразу (13-1)б побудову годографа D(j ) починають з побудови годографів Ri (j ) та Qi (j ) окремих ланок. Після цього будують годографи
R(j ) і Q(j ) шляхом перемноження годографів Ri (j ) та Qi (j ) відповідно.
Годографи перемножують за звичайним правилом множення векторів, як і при побудові частотних характеристик послідовності ланок за характеристиками окремих ланок. Для кожного значення модулі (величини векторів, проведених з початку координат у відповідну точку годографів)
перемножують, а аргументи (фази цих векторів) складають.
Дисципліна: Радіоавтоматика. Лекція 2.2. |
9 |
Зауважимо при цьому, що для звичайних типових ланок (за виключенням таких, що диференціюють) дорівнюють просто коефіцієнту передачі ланки ki й, відповідно, у системи, що складається з таких ланок, годограф R(j )= k , тобто замість його побудови для отримання годографа D(j ) достатньо просто зсунути раніше побудований годограф
Qi (j ) вправо на величину k .
5. Критерій стійкості Найквіста
Цей критерій, запропонований у 1932 році американським вченим Г.
Найквістом, дозволяю судити про стійкість замкнутої системи за амплітудно-
фазовою частотною характеристикою (а.ф.ч.х.) W(j ) розімкненої системи
(рис. 13-2, а).
Дисципліна: Радіоавтоматика. Лекція 2.2. |
10 |
Рис. 13-2. До критерію стійкості Г. Найквіста Розглянемо спершу цей критерій для випадку, коли відомо, що система
у розімкненому стані є стійкою. Умова стійкості замкненої системи у цьому разі зводиться до вимоги, щоб а.ф.ч.х. розімкненої системи не охоплювала точку (_1, j0).
На рис. 13-2, а характеристики 1 і 4 відповідають стійким системам,
характеристика 3 нестійкій, а характеристика…