
- •І.Вступ
- •Історичні відомості
- •Іі. Теоретична частина
- •2.1 Особливості формування і засвоєння основних понять теорії комплексних чисел.
- •Основні поняття теорії комплексних чисел:
- •2.2. Поняття розширення числа.
- •2.3. Розширення множини дійсних чисел. Поняття комплексного числа.
- •2.4 Дії над комплексними числами в алгебраїчній формі
- •2.4.1. Додавання комплексних чисел.
- •2.4.2. Віднімання комплексних чисел.
- •2.4.3. Множення комплексних чисел.
- •2.4.4. Ділення комплексних чисел.
- •2.4.5. Піднесення до степеня уявної одиниці.
- •2.4.6. Квадратний корінь з комплексного числа.
- •2.4.7. Властивості спряжених комплексних чисел.
- •2.5 Теорія комплексних чисел як упорядкованих пар дійсних чисел.
- •2.6 Геометрична інтерпретація комплексних чисел.
- •2.6.1. Зображення комплексних чисел точками на площині
- •2.6.2. Векторна інтерпретація операцій з комплексними числами
- •2.7. Тригонометрична форма комплексного числа. Модуль і аргумент комплексного числа
- •2.7.1. Полярні координати точки і її радіус-вектора
- •2.7.2. Модуль комплексного числа.
2.7.2. Модуль комплексного числа.
Модулем
комплексного числа
 ,
де
,
де називається число
називається число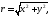 тобто
тобто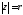 .
.
Властивості:
Якщо
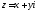 ,
де
,
де
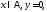 то
то
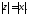
Доведення цієї властивості випливає з означення модуля комплексного числа.
Таким чином, поняття модуля комплексного числа є розвитком і узагальненням поняття модуля дійсного числа.
Модуль комплексного числа дорівнює модулю протилежного і спряженого цього числа чисел.
Доведення.
Розглянемо комплексне число
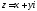 ,
де
,
де
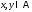 ,
а також протилежне
,
а також протилежне
 і спряжене
і спряжене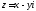 йому числа. Знайдемо їх модулі:
йому числа. Знайдемо їх модулі:
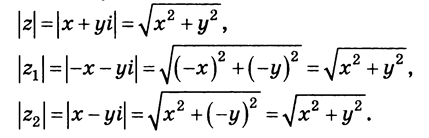
Властивість доведено.
Число
 дорівнює модулю (довжині) вектора
дорівнює модулю (довжині) вектора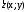 ,
тобто
,
тобто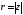 .
.
Наприклад:
Знайдіть
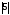 .
Так як 5 – дійсне число, то з властивості
1 отримуємо
.
Так як 5 – дійсне число, то з властивості
1 отримуємо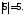
Знайдіть
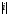 .
Запишемо числоі
в алгебраїчній формі -
.
Запишемо числоі
в алгебраїчній формі -
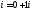 .
Тоді з означення модуля комплексного
числа, отримаємо:
.
Тоді з означення модуля комплексного
числа, отримаємо: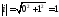 .
.Знайдіть
 .
Це число представлене в алгебраїчній
формі. З означення модуля комплексного
числа отримаємо:
.
Це число представлене в алгебраїчній
формі. З означення модуля комплексного
числа отримаємо: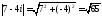 .
.Покажіть на комплексній площині всі комплексні числа з модулем, рівним
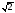 .
Всі комплексні числа з модулем
.
Всі комплексні числа з модулем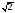 зображуються точками комплексної
площини, які є кінцями радіус – векторів
довжини
зображуються точками комплексної
площини, які є кінцями радіус – векторів
довжини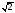 .
Множиною таких точок є коло з центром
у початку координат і радіусу
.
Множиною таких точок є коло з центром
у початку координат і радіусу (мал.10)
(мал.10)
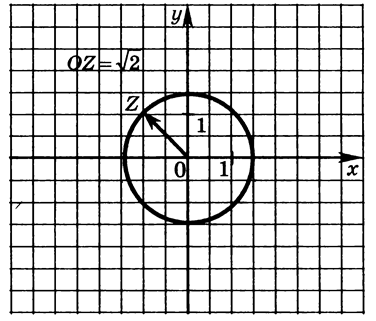
мал.10
Не порушуючи спільності міркувань, можна зробити наступний висновок.
Зображення
множини комплексних чисел з модулем
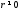 на комплексній площині є коло з центром
на початку координат і радіусом
на комплексній площині є коло з центром
на початку координат і радіусом .
.
Доказ
цього твердження полягає в послідовному
застосуванні визначення модуля
комплексного числа і визначення кола
з центром на початку координат і радіусом
 .
.
Наприклад:
Зобразіть на комплексній площині всі комплексні числа з модулем, меншим або рівним 2.
Всі комплексні числа з модулем, меншим або рівним 2, зображуються точками комплексної площині, які є кінцями радіус-векторів довжини, менше рівної 2. Безліч таких точок є коло з центром на початку координат і радіусом 2. (мал.11)
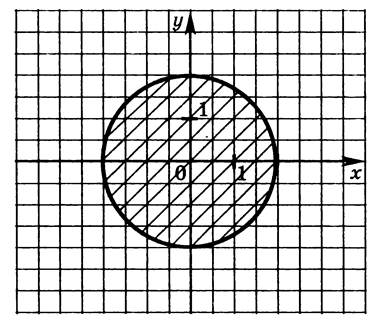
мал.11
Зобразіть на комплексній площині всі комплексні числа, що задовольняють умові:
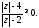
У цьому завданні розглядаються всі точки площини, крім точок, розташованих між концентричними колами і на меншому колі. Центри кіл - початок координат, радіуси рівні 2 і 4. (мал.12)
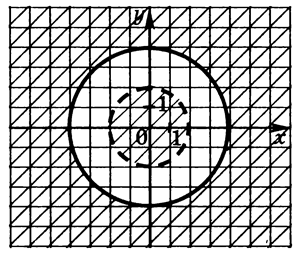
мал.12
Аргумент комплексного числа
Радіус
– вектор точки
 комплексної площини задається двома
числами:
комплексної площини задається двома
числами: -довжина
(модуль) вектора,
-довжина
(модуль) вектора,
 - кут між вектором і додатним направленням
вісіОх.
- кут між вектором і додатним направленням
вісіОх.
Якщо
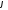 - аргумент комплексного числа, то будь
– яке число виду
- аргумент комплексного числа, то будь
– яке число виду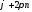 ,
де
,
де ,
також є аргументом даного числа
,
також є аргументом даного числа .
Вірно і зворотне твердження: якщо число
.
Вірно і зворотне твердження: якщо число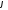 є аргументом даного комплексного числа
є аргументом даного комплексного числа ,
то воно можна подати у вигляді
,
то воно можна подати у вигляді ,
де
,
де - деяке ціле число. Обидва твердження
очевидним чином випливають з властивостей
періодичності тригонометричних функцій.
- деяке ціле число. Обидва твердження
очевидним чином випливають з властивостей
періодичності тригонометричних функцій.
Два
ненульових комплексних числа рівні
тоді і тільки тоді, коли їх модулі рівні,
а аргументи відрізняються на
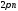 ,
де
,
де .
.
Наприклад:
Зобразіть на комплексній площині всі комплексні числа з аргументом

Усі
комплексні числа з аргументом
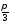 зображуються точками комплексної
площини, які є кінцями ненульових радіус
– векторів, утворюють з додатним
направленням вісі абсцис кут
зображуються точками комплексної
площини, які є кінцями ненульових радіус
– векторів, утворюють з додатним
направленням вісі абсцис кут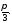 Множиною таких точок являється промінь
Множиною таких точок являється промінь ,
який утворює з додатним направленням
вісі абсцис кут
,
який утворює з додатним направленням
вісі абсцис кут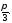 Зауважимо, що при цьому мається на увазі
промінь без початкової точки (мал.13).
Зауважимо, що при цьому мається на увазі
промінь без початкової точки (мал.13).
мал.13
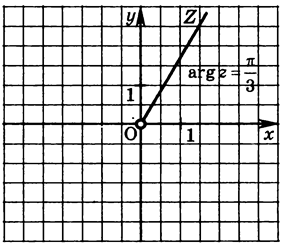
Зобразіть на комплексній площині всі комплексні числа з аргументом
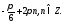
Всі
комплексні числа з аргументом
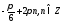 зображуються точками комплексної
площини, які є кінцями ненульових радіус
– векторів, утворюють з додатним
направленням вісі абсцис кут
зображуються точками комплексної
площини, які є кінцями ненульових радіус
– векторів, утворюють з додатним
направленням вісі абсцис кут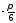 .
Множиною таких точок являється промінь
.
Множиною таких точок являється промінь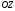 ,
який утворює з додатним направленням
вісі абсцис кут
,
який утворює з додатним направленням
вісі абсцис кут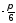 .
(мал.14)
.
(мал.14)
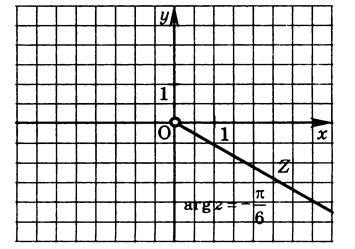
мал.14
Зобразіть на комплексній площині всі комплексні числа з аргументами
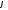 такими, що
такими, що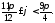
Всі
комплексні числа з вказаними аргументами
зображується точками комплексної
площини, розташованими нижче промінів
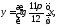
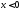 і
і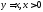 .
Цей кут без однієї з сторін та вершини
(мал.15) .
.
Цей кут без однієї з сторін та вершини
(мал.15) .
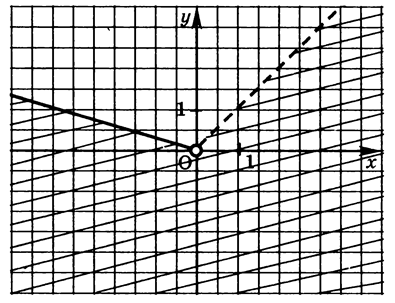
мал.15
Тригонометрична форма комплексного числа.
Розглянемо на комплексній площині числа з модулем 1. Зображенням множини таких чисел являється коло з центром у початку координат та радіусом 1 (мал.16).
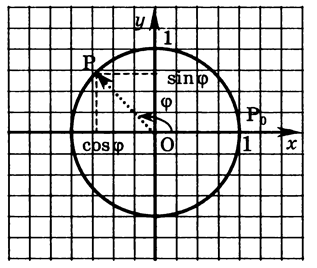
мал. 16
Нехай
т. - точка перетину кола з позитивним
напрямом осі абсцис. Розглянемо точкуР
кола, що зображує деякий комплексне
число
- точка перетину кола з позитивним
напрямом осі абсцис. Розглянемо точкуР
кола, що зображує деякий комплексне
число
 .
ТочкаР
є образом точки
.
ТочкаР
є образом точки
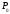 при повороті з центромО
на кут
при повороті з центромО
на кут
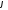 ,
причому кут визначений з точністю до
,
причому кут визначений з точністю до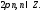 Тоді абсцисах
точки Р
дорівнює
Тоді абсцисах
точки Р
дорівнює
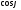 ,
а ординатау
дорівнює
,
а ординатау
дорівнює
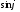 .
Тому комплексне число
.
Тому комплексне число задається формулою
задається формулою
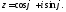
Зараз
розглянемо довільне, відмінне від нуля,
комплексне число
 з модулем
з модулем ,
,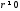 .
Тоді
.
Тоді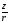 - комплексне число, модуль якого дорівнює
1. Тому існує число
- комплексне число, модуль якого дорівнює
1. Тому існує число таке, що
таке, що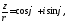 тобто
тобто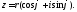
Запис
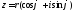 при
при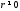 називається тригонометричною формою
комплексного числа
називається тригонометричною формою
комплексного числа .
.
Числа
 і
і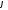 називаютьсямодулем
і
аргументом
комплексного числа
називаютьсямодулем
і
аргументом
комплексного числа
 .
Для модуля та аргументу використовуються
також позначення:
.
Для модуля та аргументу використовуються
також позначення: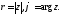 Зазвичай вибирають значення
Зазвичай вибирають значення ,
визначене нерівністю
,
визначене нерівністю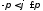 .
.
