
- •І.Вступ
- •Історичні відомості
- •Іі. Теоретична частина
- •2.1 Особливості формування і засвоєння основних понять теорії комплексних чисел.
- •Основні поняття теорії комплексних чисел:
- •2.2. Поняття розширення числа.
- •2.3. Розширення множини дійсних чисел. Поняття комплексного числа.
- •2.4 Дії над комплексними числами в алгебраїчній формі
- •2.4.1. Додавання комплексних чисел.
- •2.4.2. Віднімання комплексних чисел.
- •2.4.3. Множення комплексних чисел.
- •2.4.4. Ділення комплексних чисел.
- •2.4.5. Піднесення до степеня уявної одиниці.
- •2.4.6. Квадратний корінь з комплексного числа.
- •2.4.7. Властивості спряжених комплексних чисел.
- •2.5 Теорія комплексних чисел як упорядкованих пар дійсних чисел.
- •2.6 Геометрична інтерпретація комплексних чисел.
- •2.6.1. Зображення комплексних чисел точками на площині
- •2.6.2. Векторна інтерпретація операцій з комплексними числами
- •2.7. Тригонометрична форма комплексного числа. Модуль і аргумент комплексного числа
- •2.7.1. Полярні координати точки і її радіус-вектора
- •2.7.2. Модуль комплексного числа.
2.4 Дії над комплексними числами в алгебраїчній формі
2.4.1. Додавання комплексних чисел.
Сумою двох або кількох комплексних чисел називається комплексне число, дійсна частина якого дорівнює сумі дійсних частин доданків, а коефіцієнт уявної частини дорівнює сумі коефіцієнтів уявних частин доданків.

Наприклад:

В області дійсних чисел є число "нуль", додавання якого до будь – якого іншого дійсного числа не змінює його.
В
області комплексних чисел аналогічну
роль відіграє число
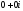 .
Справді, яким би не було комплексне
число
.
Справді, яким би не було комплексне
число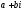 ,
, .
.
З
курсу математики ми знаємо, що сума двох
дійсних чисел а і –а дорівнює нулю і
вони називаються протилежними. Аналогічно
з цим, комплексні числа
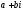 і
і також називаються протилежними:
також називаються протилежними: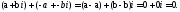
Наприклад:
 .
.
Додавання
комплексних чисел підлягає асоціативному
і комутативному законам:
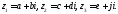
комутативність:
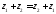 .
.
 .
.
асоціативність
 .
.
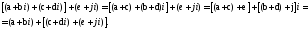
2.4.2. Віднімання комплексних чисел.
Різницею комплексних чисел є комплексне число, дійсна частина якого дорівнює різниці дійсних частин зменшуваного і від’ємника, а коефіцієнт уявної частини дорівнює різниці коефіцієнтів уявних частин зменшуваного і від’ємника.

Наприклад:
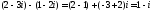 .
.
Тобто від кожного комплексного числа можна відняти будь – яке інше комплексне число. Віднімання – це дія обернена додавання. Можливість такого віднімання і його однозначність потребує доведення.
Доведення.
 а
різницю цих чисел позначимо
а
різницю цих чисел позначимо
 .
Доведемо, що для будь – яких комплексних
чисел
.
Доведемо, що для будь – яких комплексних
чисел і
і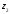 різниця
різниця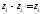 визначена і притому однозначно.
визначена і притому однозначно.
Фактично
нам потрібно довести, що існує, і при
тому тільки єдине, комплексне число
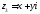 ,
яке в сумі з
,
яке в сумі з дає
дає :
:
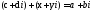 (3)
(3)
За означенням суми комплексних чисел:
 .
.
Тому рівняння (3) можна переписати у вигляді

Два комплексних числа рівні тоді і тільки тоді, коли рівні їх дійсні частини і коефіцієнти при уявних частинах. Тому

Ця система рівнянь завжди має розв’язок і притому єдиний:
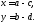
Таким
чином, існує і при тому єдина пара дійсних
чисел (х;у), що задовольняє рівняння (3).
Отже, ми довели, що

Щоб від одного комплексного числа відняти друге, досить це віднімання виконати окремо для дійсних частин цих чисел і коефіцієнтів при уявних частинах.
Наприклад:
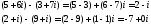
2.4.3. Множення комплексних чисел.
Два
комплексних числа перемножуються за
допомогою правил множення многочленів
в алгебрі, слід тільки пам’ятати, що
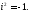 Таким чином
Таким чином
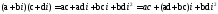
Але
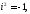 тому
тому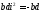 і отже,
і отже, (4)
(4)
Цю формулу (4) й покладено в основу означення добутку двох комплексних чисел.
Добутком
двох комплексних чисел
 і
і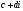 називається таке комплексне число:
називається таке комплексне число:
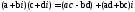
Наприклад:
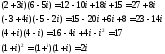
Висновок:
 .
.
Властивості множення комплексних чисел:
комутативність

асоціативність

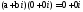
2.4.4. Ділення комплексних чисел.
Часткою
від ділення комплексного числа
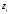 на комплексне число
на комплексне число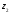 називається таке число
називається таке число ,
яке при множені на
,
яке при множені на дає
дає .
.
Доведемо,
що частка
 визначена і при чому однозначно для
всіх комплексних чисел
визначена і при чому однозначно для
всіх комплексних чисел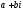 і
і ,
якщо
,
якщо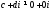 .
.
Нам потрібно довести, що існує і при чому єдина пара дійсних чисел (х;у), що задовольняє рівнянню:
 .
(5)
.
(5)
По правилу множення комплексних чисел:
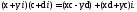
Тому рівняння (5) можна переписати у вигляді:
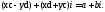
А з умови рівності двох комплексних чисел маємо:


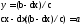
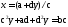

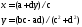
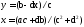
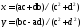
Таким чином,
 .
.
Ця
формула має зміст, якщо
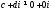 .
Отже ділення комплексних чисел можливе,
якщо дільник не дорівнює нулю.
.
Отже ділення комплексних чисел можливе,
якщо дільник не дорівнює нулю.
Легко перевірити, що правило ділення комплексних чисел можна одержати, якщо помножити ділене і дільник на число, спряжене з дільником:

Наприклад:

