
- •І.Вступ
- •Історичні відомості
- •Іі. Теоретична частина
- •2.1 Особливості формування і засвоєння основних понять теорії комплексних чисел.
- •Основні поняття теорії комплексних чисел:
- •2.2. Поняття розширення числа.
- •2.3. Розширення множини дійсних чисел. Поняття комплексного числа.
- •2.4 Дії над комплексними числами в алгебраїчній формі
- •2.4.1. Додавання комплексних чисел.
- •2.4.2. Віднімання комплексних чисел.
- •2.4.3. Множення комплексних чисел.
- •2.4.4. Ділення комплексних чисел.
- •2.4.5. Піднесення до степеня уявної одиниці.
- •2.4.6. Квадратний корінь з комплексного числа.
- •2.4.7. Властивості спряжених комплексних чисел.
- •2.5 Теорія комплексних чисел як упорядкованих пар дійсних чисел.
- •2.6 Геометрична інтерпретація комплексних чисел.
- •2.6.1. Зображення комплексних чисел точками на площині
- •2.6.2. Векторна інтерпретація операцій з комплексними числами
- •2.7. Тригонометрична форма комплексного числа. Модуль і аргумент комплексного числа
- •2.7.1. Полярні координати точки і її радіус-вектора
- •2.7.2. Модуль комплексного числа.
2.6 Геометрична інтерпретація комплексних чисел.
2.6.1. Зображення комплексних чисел точками на площині
Розглянемо
площину з введеною на ній прямокутною
декартовою системою координат. Поставимо
у відповідність кожному комплексному
числу
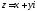 (х
і у
– дійсні числа) у відповідність точку
(х
і у
– дійсні числа) у відповідність точку
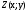 координатної площини. Зауважимо, що
встановлену відповідність між безліччю
комплексних чисел і множиною точок
координатної площини взаємно однозначно.
Зауважимо також, що кожній точці
координатної площини. Зауважимо, що
встановлену відповідність між безліччю
комплексних чисел і множиною точок
координатної площини взаємно однозначно.
Зауважимо також, що кожній точці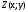 координатної площини поставлений у
відповідність радіус – вектор
координатної площини поставлений у
відповідність радіус – вектор (мал.3), координати якого співпадають з
координатами точкиZ.
(мал.3), координати якого співпадають з
координатами точкиZ.

мал.3
Площина, на якій зображуються у вигляді точок комплексні числа, називається комплексною площиною.
Будь-якому
дійсному числу відповідає точка
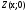 а
будь-якому суто уявному числу відповідає
точка
а
будь-якому суто уявному числу відповідає
точка .
Тому всі дійсні числа зображуються
точками осі абсцис, яка називаєтьсядійсною
віссю, а все чисто уявні числа зображуються
точками осі ординат, яка називається
уявною
віссю.
.
Тому всі дійсні числа зображуються
точками осі абсцис, яка називаєтьсядійсною
віссю, а все чисто уявні числа зображуються
точками осі ординат, яка називається
уявною
віссю.
Наприклад:
1.
Зобразіть на комплексній площині число
 .
.
Цьому числу відповідає точка комплексної площини з координатами (3;-2), мал.4.
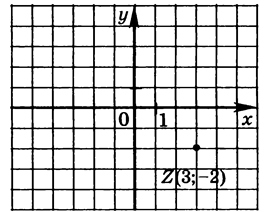
мал.4
2.
Зобразіть на комплексній площині всі
комплексні числа z,
для яких вірно рівність
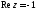 .
.
Це всі числа, які знаходяться на прямій, заданій наступною умовою х=-1, мал.5.
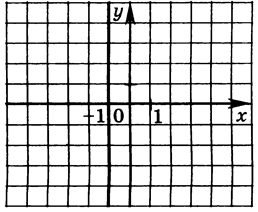
мал.5
2.6.2. Векторна інтерпретація операцій з комплексними числами
Проілюструємо операції додавання і віднімання комплексних чисел на комплексній площині.
Нехай
дані комплексні числа
 і
і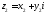 .
Як відомо, їх сума теж комплексне число:
.
Як відомо, їх сума теж комплексне число: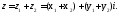 Розглянемо відповідні числам
Розглянемо відповідні числам ,
,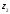 і
і радіус – вектори
радіус – вектори і
і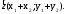 Тоді
Тоді
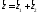 .
Нехай вектори
.
Нехай вектори ,
, не
колінеарні. Так як вони мають спільний
початок – початок координат т.О, то їх
суму – вектор
не
колінеарні. Так як вони мають спільний
початок – початок координат т.О, то їх
суму – вектор можна побудувати за допомогою правила
паралелограма (мал.6). Кінець цього
вектору – точка
можна побудувати за допомогою правила
паралелограма (мал.6). Кінець цього
вектору – точка - зображення комплексного числа
- зображення комплексного числа
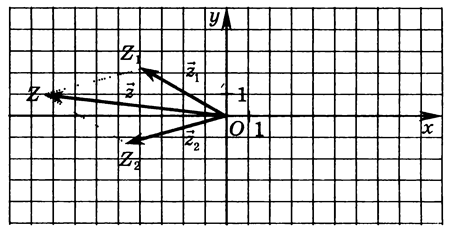
мал.6
Розглянемо
віднімання комплексних чисел
 і
і .
Вона дорівнює комплексному числу
.
Вона дорівнює комплексному числу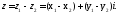 Розглянемо
відповідні числам
Розглянемо
відповідні числам
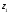 ,
, і
і радіус – вектори
радіус – вектори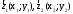 і
і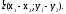 Тоді
Тоді
 .
Вектори
.
Вектори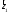 і
і мають спільний початок – початок
координат т.О. Побудуємо їх різницю –
вектор
мають спільний початок – початок
координат т.О. Побудуємо їх різницю –
вектор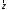 - і відкладемо його від початку координат
(мал. 7). Кінець цього вектора – точкаZ
– зображення числа
- і відкладемо його від початку координат
(мал. 7). Кінець цього вектора – точкаZ
– зображення числа
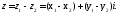
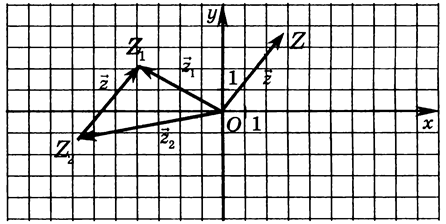
мал. 7
2.7. Тригонометрична форма комплексного числа. Модуль і аргумент комплексного числа
2.7.1. Полярні координати точки і її радіус-вектора
Кожному
комплексному числу
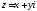 може бути поставлена у співвідношення
точку
може бути поставлена у співвідношення
точку на комплексній площині, а кожній точці
– радіус – вектор
на комплексній площині, а кожній точці
– радіус – вектор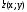 .
.
Точку
Z
можна задати також іншою парою чисел
- полярними координатами:
 - відстань від початку координат (т.О)
та кутом
- відстань від початку координат (т.О)
та кутом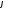 між променемOZ
та додатним направленням вісі абсцис
(мал. 8).
між променемOZ
та додатним направленням вісі абсцис
(мал. 8).

мал.8
Відповідно
радіус – вектор точки Z
задається тими ж числами, тобто
 ,
деr
– довжина (модуль) вектора,
,
деr
– довжина (модуль) вектора,
 - кут між вектором і віссю ОХ.
- кут між вектором і віссю ОХ.
Для подальшого вивчення комплексних чисел нам необхідно згадати деякі властивості векторів:
Модуль (довжина) вектора
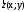 дорівнює
дорівнює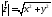 .
.Кут між радіус-вектором і додатним напрямком осі абсцис - це кут повороту, при якому додатний напрям осі абсцис переходить в промінь, що задає напрямок даного вектора, при цьому початок променя є початок координат. Кут вважається додатним при повороті проти годинникової стрілки і від’ємним при повороті за годинниковою стрілкою.
Наприклад:
В координатній площині задані вектори
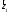 і
і (мал. 9). Знайдіть їх модулі (довжини). Які
кути вони утворюють з додатним направленням
вісі абсцис?
(мал. 9). Знайдіть їх модулі (довжини). Які
кути вони утворюють з додатним направленням
вісі абсцис?
Так
як
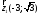 ,
,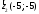 ,
то
,
то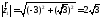 ,
,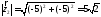 .
Промінь
.
Промінь є образом променяОх
при повороті на кут, який дорівнює
є образом променяОх
при повороті на кут, який дорівнює
 ,
а також при повороті на кут
,
а також при повороті на кут ,
або
,
або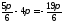 і так далі.
і так далі.
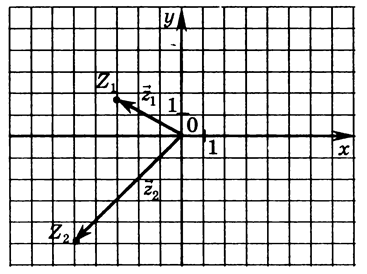
мал. 9
Тому
вірне твердження, що вектор
 утворює з додатним направленням вісі
абсцис кут
утворює з додатним направленням вісі
абсцис кут ,
де
,
де - будь – яке ціле число.
- будь – яке ціле число.
Аналогічним
чином визначаємо, що вектор
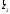 утворює з додатним направленням вісі
абсцис кут
утворює з додатним направленням вісі
абсцис кут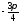 ,
або
,
або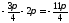 ,
або
,
або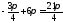 і так далі, тобто
і так далі, тобто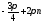 .
.
Відповідь:
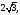

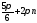 ,
, ,
де
,
де - будь – яке ціле число.
- будь – яке ціле число.
Нульовий вектор однозначно визначається модулем (довжиною), тобто кут між нульовим вектором і позитивний напрямом осі Ох не розглядається. Модуль нульового вектора дорівнює 0.
Нехай вектор
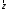 у прямокутній декартовій системі
координат має координатих
і у
та утворює з додатним направленням
вісі абсцис кут
у прямокутній декартовій системі
координат має координатих
і у
та утворює з додатним направленням
вісі абсцис кут
 .
Тоді
.
Тоді
 .
.
