
- •І.Вступ
- •Історичні відомості
- •Іі. Теоретична частина
- •2.1 Особливості формування і засвоєння основних понять теорії комплексних чисел.
- •Основні поняття теорії комплексних чисел:
- •2.2. Поняття розширення числа.
- •2.3. Розширення множини дійсних чисел. Поняття комплексного числа.
- •2.4 Дії над комплексними числами в алгебраїчній формі
- •2.4.1. Додавання комплексних чисел.
- •2.4.2. Віднімання комплексних чисел.
- •2.4.3. Множення комплексних чисел.
- •2.4.4. Ділення комплексних чисел.
- •2.4.5. Піднесення до степеня уявної одиниці.
- •2.4.6. Квадратний корінь з комплексного числа.
- •2.4.7. Властивості спряжених комплексних чисел.
- •2.5 Теорія комплексних чисел як упорядкованих пар дійсних чисел.
- •2.6 Геометрична інтерпретація комплексних чисел.
- •2.6.1. Зображення комплексних чисел точками на площині
- •2.6.2. Векторна інтерпретація операцій з комплексними числами
- •2.7. Тригонометрична форма комплексного числа. Модуль і аргумент комплексного числа
- •2.7.1. Полярні координати точки і її радіус-вектора
- •2.7.2. Модуль комплексного числа.
2.2. Поняття розширення числа.
Одним з основних понять математики є поняття числа. Спочатку, в процесі рахування предметів, склалося поняття цілого додатного (натурального) числа – це поняття являється відображенням в свідомості людини кількісної сторони кінцевих зібрань (множин) предметів. Але вже найпростіші записи практики вчених, пов’язаних з вимірюваннями, привели до розширення поняття числа. Саме під впливом цих записів поступово склалося поняття додатного раціонального (дробового) числа і ірраціонального числа.
Але
по іншому формувалося поняття від’ємного
числа. Воно з’явилося під впливом
внутрішніх потреб самої математики, в
зв’язку з необхідністю зробити рівняння
виду:
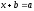 розв’язуючим, навіть тоді, коли
розв’язуючим, навіть тоді, коли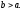
Перші згадування про від’ємні числа і дії над ними зустрічаються у індійських математиків в VII ст. нашої ери. Їм також належить загальне теперішнє пояснення від’ємних і додатних чисел як арифметичних образів протилежно направлених величин. Саме це пояснення особливо сприяло тому, щоб поняття від’ємного числа стало рівноправним з поняттям додатного числа.
Кожне нове розширення поняття числа дозволяло розв’язувати такі задачі, які до цього були нерозв’язними. Так введення дробів дозволило виконати ділення двох чисел у всіх випадках, коли дільник не дорівнює нулю; введення від’ємних чисел дозволило проводити у всіх випадках віднімання; введення ірраціональних чисел дозволило виразити числом довжину відрізка, яка є несумірною з даною одиницею довжини.
Із курсу алгебри відомо, що числа цілі і дробові, як додатні так і від’ємні, і нуль називаються раціональними числами.
Нескінченні і періодичні десяткові дроби називаються ірраціональними числами.
Множина раціональних і ірраціональних чисел утворює множину дійсних чисел.
Поняття
числа пройшло довгий шлях історичного
розвитку. Однією з найпростіших числових
множин є множина натуральних чисел: 1,
2, 3…. В ній завжди виконуються дві
алгебраїчні дії: додавання і множення.
Це означає, що, які б не були числа
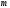 і
і їх сума
їх сума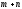 і добуток
і добуток неодмінно є натуральними числами. При
чому справджуються такі п’ять законів:
неодмінно є натуральними числами. При
чому справджуються такі п’ять законів:
комутативний закон додавання –
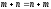 ;
;асоціативний закон додавання –
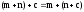 ;
;комутативний закон множення –
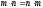 ;
;асоціативний закон множення –
 ;
;дистрибутивний закон множення відносно додавання –
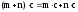 .
.
Що
ж до віднімання і ділення, то ці дві дії
в множині натуральних чисел здійснюється
не завжди. Так жодну з різниць
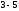 або
або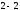 , або жодну з часток
, або жодну з часток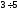 і
і ніяк не можна назвати натуральним
числом.
ніяк не можна назвати натуральним
числом.
Щоб
віднімання завжди виконувалося, множину
натуральних чисел потрібно було доповнити
множину всіх від’ємних цілих чисел з
нулем. В результаті такого доповнення
або розширення ми переходимо до множини
цілих чисел:
 .
.
Числова множина, в якій завжди здійснені операції додавання і множення, що підлягають вказаним вище п’ятьом законам, а також віднімання, називаються кільцем. Таким чином, множина всіх цілих чисел утворює кільце.
Розширивши
множину всіх натуральних чисел, ми
показали, з підручників, що дія віднімання
може здійснюватися завжди. Але ділення
так і залишилося невизначеним. Щоб
усунути цю прогалину, треба розширити
і множину цілих чисел. Зробити це можливо
лише за допомогою приєднання множини
звичайних дробів, тобто
 , де
, де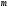 і
і - довільні цілі числа, і
- довільні цілі числа, і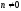 .
В результаті такого розширення ми
отримуємо множину раціональних чисел.
В цій множині завжди виконуються усі
чотири дії: додавання, віднімання,
множення і ділення.
.
В результаті такого розширення ми
отримуємо множину раціональних чисел.
В цій множині завжди виконуються усі
чотири дії: додавання, віднімання,
множення і ділення.
Множина чисел, в якій завжди здійснені дії додавання і множення, що підлягають п’ятьом основним законам, а також дії віднімання і ділення (крім ділення на нуль) називається полем. Множина раціональних чисел є найпростішим числовим полем.
Зауважимо,
що множина ірраціональних чисел не є
полем. Будь – яка з чотирьох дій над
ірраціональними числами може привести
до раціонального числа. Наприклад:

У множині дійсних чисел завжди можливі всі шість алгебраїчних операцій: додавання, віднімання, множення, ділення, піднесення до степеня і добування кореня парного степеня з додатного числа.
