12.9.Поляризація хвилі

Лінійна поляризація. Площина, утворена векторами хвилі, називається площиною поляризації хвилі. Якщо площина поляризації зберігає своє положення в просторі, то така хвиля є лінійно поляризованою (плоско поляризованою).

Еліптична поляризація. Якщо в площині  , вершина вектораописує еліпс, то така хвиля еліптично поляризована. Це означає, що вектормає дві складові, зсунуті по фазі

. (1)

В цьому випадку можна розглянути задачу додавання двох взаємно перпендикулярних коливань із зсувом по фазі, результатом якого маємо рівняння для траєкторії, яку описує вершина вектора з часом

+- 2cos = sin². (2)

Для випадку  = (2m +1) траєкторіями є еліпси. Коли ж ще й А₁ = А₂, то еліпси перетворюються в кола і така хвиля називається циркулярно поляризованою (поляризованою по колу).

Природна поляризація. Якщо в площині перпендикулярній вектору вектор кожної миті займає рівно ймовірні напрямки, то така хвиля називається природно поляризованою.

12.10. Енергія, інтенсивність та тиск електромагнітної хвилі

Об'ємна густина енергії електромагнітного поля w дорівнює сумі об'ємних густин енергії електричного w_е та магнітного w_m полів

. (1)

Зважаючи на рівність Н= Е, одержимо

, (2)

де - швидкість розповсюдження електромагнітної хвилі в середовищі,-показник заломлення середовища,- швидкість розповсюдження електромагнітної хвилі в вакуумі.

Для плоскої монохроматичної хвилі , маємо

. (3)

Середнє за період Т значення густини енергії

, (4)

тому, що

.

Вектор називається вектором Пойнтінга. Цей вектор є вектором потоку енергії, який можна записати у вигляді .Промінь електромагнітної хвилі є уявна крива, дотична до якої вказує напрямок розповсюдження енергії, тобто напрямок вектора . Для ізотропного середовища цей напрямок співпадає з напрямком швидкості хвилі.

Модуль вектора називається інтенсивністю І електромагнітної хвилі і він чисельно дорівнює енергії, що розповсюджується за 1с через поперечний переріз в 1м². Для плоскої монохроматичної хвилі з амплітудою

, (5)

або

,

де амплітуда магнітної складової.

За розрахунками Максвелла електромагнітна хвиля, що падає на поверхню під кутом , утворює тиск на поверхню падіння

,

де R - коефіцієнт відбиття енергії. Покажемо це в такий спосіб. Нехай на поверхню S за одиницю часу падає  поверхні S випромінювання, яке має густину енергії <w>. Імпульс випромінювання

. (6)

При відбиванні від поверхні з коефіцієнтом відбивання R, випромінювання передає їй імпульс рівний

, (7)

а решта поглинутої енергії (1 - R) випромінювання передає імпульс

. (9)

Разом поверхні буде передано імпульс

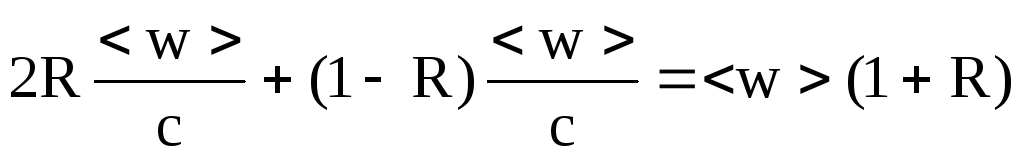. (10)

За другим законом Ньютона імпульс, переданий одиничній поверхні за одиницю часу, чисельно рівний тиску, тому тиск що його створює електромагнітна хвиля запишеться так

Р = (1 +R). (11)

При падінні випромінювання під кутом , потрібно ввести множник, тому що тиск створює нормальна складова випромінювання.