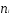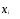2. Знаходження точкових оцінок математичних сподівань і дисперсій генеральних сукупностей

Точкові оцінки невідомих параметрів розподілу можна знайти методом найбільшої правдоподібності, який зводиться до знаходження максимуму функції одного або декількох аргументів (параметрів).

Розглядаємо множину Х

Нам відомі суми частот варіант інтервалів (табл. 3)

Таблиця 3

Частковий інтервал	Сума частот варіант інтервалу,
-1,744 - -1,50	7
-1,150 - -0,555	9
-0,555 - 0,039	11
0,039 - 0,633	13
0,633 - 1,228	7
1,228 - 3,011	3

Вибираємо середини відрізків інтервалів, які створюють послідовність рівновіддалених варіант (табл. 4)

Таблиця 4

Частковий інтервал,	Сума частот варіант інтервалу,
-1,447	7
-0,853	9
-0,258	11
0,336	13
0,930	7
2,119	3

Складаємо розрахункову таблицю, для чого:

1. запишемо варіанти в перший стовпець;

2. запишемо частоти в другий стовпець і суму частот n=50 помістимо в нижню клітину стовпця; у якості фальшивого нуля С виберемо варіанту 0,336, яка розміщена посередині варіаційного ряду, і розрахуємо умовні варіанти , де.

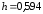3. добутки частот на умовні варіанти n_iu_i записуємо в четвертий стовпець. Окремо знаходимо суму чисел. Складемо ці числа і їх суму поміщаємо в нижню клітинку стовпця;

4. добуток частот на квадрати умовних варіант запишемо в п’ятий стовпець. Суму чисел стовпця поміщаємо в нижню клітинку стовпця;

5. добутки частот на квадрати умовних варіант, збільшених на одиницю, записуємо в шостий контрольний стовпець. Суму чисел стовпця поміщаємо в нижню клітинку стовпця.

(Таблиці створююю у Excel, там же виконую розрахунки.)

Таблиця 5

	ni	ui	niui	niui2	ni(ui+1)2
-1,447	7	-3	-21	63	28
-0,853	9	-2	-18	36	9
-0,258	11	-1	-11	11	0
0,336	13	0	0	0	13
0,930	7	1	7	7	28
2,119	3	3	9	27	48
	n=50		Σ niui =-34	Σ niui2=144	Σni(ui+1)2=126

Виконаємо контроль отриманих результатів:

∑n_iu_i²+2∑n_iu_i+n = 144-2*34+50=126;

∑n_i(u_i+1)²= 126;

Отже, обчислення виконані правильно.

Обчислимо умовні моменти першого і другого порядків:

M₁^*=∑n_iu_i / n = -34/50 = -0,68;

M₂^*=∑n_iu_i² / n = 144/50 = 2,88;

Обчислимо вибіркові середнє і дисперсію:

_в=М₁^*h + C = -0,68*0.594+0,336 = -0,068;

D_a = (M₂^* - (M₁^*)²)*h² = (2,88 –(-0,68*-0,68))0,594*0,594 = 0,854;

Аналогічно розглядаємо множину Y

Нам відомі суми частот варіант інтервалів (табл. 6)

Таблиця 6

Частковий інтервал,	Сума частот варіант інтервалу,
-2,011 - -1,379	6
-1,379 - -0,747	8
-0,747 - -0,115	10
-0,115 - 0,517	10
0,517 - 1,149	8
1,149 - 1,781	5
1,781 - 3,045	3

Вибираємо середини відрізків інтервалів, які і створюють послідовність рівновіддалених варіант (табл. 7):

Таблиця 7

Частковий інтервал,	Сума частот варіант інтервалу,
-1,695	6
-1,063	8
-0,431	10
0,201	10
0,833	8
1,465	5
2,413	3

Складаємо розрахункову таблицю (табл. 8)

Таблиця 8

		ui	niui	niui2	ni(ui+1)2
-1,695	6	-3	-18	54	24
-1,063	8	-2	-16	32	8
-0,431	10	-1	-10	10	0
0,201	10	0	0	0	10
0,833	8	1	8	8	32
1,465	5	2	10	20	45
2,413	3	4	11	37	61
	n=50		Σ niui =-16	Σ niui2=161	Σni(ui+1)2=180

Виконаємо контроль отриманих результатів:

∑n_iu_i²+2∑n_iu_i+n = 161+2*-16+50 = 180;

∑n_i(u_i+1)²= 180;

Отже, обчислення виконані правильно.

Обчислимо умовні моменти першого і другого порядків:

M₁^*=∑n_iu_i / n = -16/50 = -0,31;

M₂^*=∑n_iu_i² / n = 161/50 = 3,21;

Обчислимо вибіркові середнє і дисперсію:

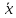_в=М₁^*h + C = -0,31*0,632+0.201 = 0,005;

D_a = (M₂^* - (M₁^*)²)*h² = (3,21 – (-0,31*-0,31))*0,632*0,632 = 1,246;

Література: [1, c. 160-174; 2, c. 229-293].