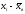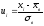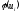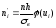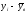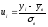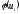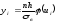3. Оцінка невідомих математичних сподівань м[х] і m[у] генеральних сукупностей х і у за допомогою довірчого інтервалу з надійністю 0,95

Необхідно оцінити невідомі математичні сподівання M[X] i M[Y] генеральних сукупностей 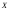іза допомогою довірчого інтервалу з надійністю 0,95.

Отже, 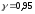, n=50. Користуючись таблицею значень (додаток 2) 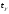знаходимо.

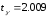Розглядаємо множину Х

Середнє квадратичне відхилення, або стандартне відхилення, являє собою квадратний корінь із дисперсії. Отже, S = 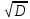==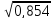 0,924;

Знаходимо вибіркове середнє: x = -0,068;

Знайдемо довірчі інтервали:

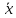–tᵧ 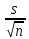= -0,068 – 2,009*(0,924/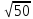) = -0,331;

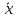+ tᵧ 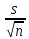= -0,068 + 2,009*(0,924/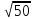) = 0,195;

Отже з надійністю 0,95 невідомий параметр математичне сподівання 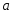знаходиться в довірчому інтервалі. -0,331 <а < 0,195;

Розглядаємо множину Y:

S = 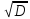==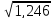 1,116;

Знаходимо вибіркове середнє: y = 0,005;

Знайдемо довірчі інтервали:

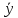–tᵧ 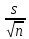= 0,005 – 2,009*(1,116/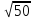) = -0,312;

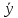+ tᵧ 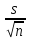= 0,005 + 2,009*(1,116/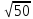) = 0,322;

Отже з надійністю 0,95 невідомий параметр математичне сподівання 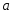знаходиться в довірчому інтервалі. -0,312 <а < 0,322;

Література: [1, c. 174-180; 2, c. 213-219].

4._Перевірка гіпотези про рівність дисперсій генеральних сукупностей для вибірок X та y

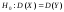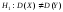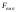Для того, щоб при заданому рівні значущості перевірити нульову гіпотезу про рівність генеральних дисперсій нормальних сукупностей при конкуруючій гіпотезі, потрібно обчислити емпіричне значення критерію, як відношення більшої виправленої дисперсії до меншої

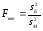
і за таблицею критичних точок розподілу Фішера-Снедекора за рівнем значущості 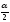(вдвічі меншим заданого) і числом ступенів вільності k₁ і k₂ (k₁ - число ступенів вільності більшої дисперсії, k₂ - число ступенів вільності меншої дисперсії) знайти критичну точку F_кр (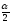;k₁,k₂). Якщо F_емп< F_кр – немає підстав відхилити нульову гіпотезу. Якщо F_емп>F_кр – нульову гіпотезу відхиляють.

Необхідно запропонувати просту гіпотезу про рівність дисперсій генеральних сукупностей 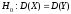при конкуруючій гіпотезі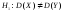. Прийнявшии рівень значущості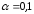, слід перевірити запропоновану гіпотезу.

Для цього знайдемо емпіричне значення критерію 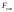як відношення більшої виправленої дисперсії до меншої.

Нагадаємо: обсяг вибірок n₁ = n₂ = 50, виправлені вибіркові дисперсі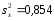ї і.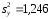

Підставимо значення та в формулу, отримаємо

F_емп= 1,246 / 0,854 = 1,459;

По таблиці Фішера-Снедекора(додаток 2), по рівню значущості, що в двічі менший за заданий, тобто при α/2 = 0,1/2 = 0,05, та кількістю степенів свободи k₁ =49 k₂ =49 знаходимо критичну точку F_кр(0,05; 49, 49) = 1,60

Так як спостережений критерій менший за критичний F_емп < F_кр (1,459 < 1,60), то немає підстави відхилити нульову гіпотезу.

Література: [1, c. 207-210; 2, c. 288-293].

5. Побудова нормальних кривих за вибірками з генеральних сукупностей х і y

Для побудови нормальної кривої необхідно визначити емпіричні і теоретичні (вирівнюючі) частоти.

Емпіричними частотами називають частоти n_i, які фактично спостерігаються.

Вирівнюючими (теоретичними) називають частоти 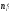, які знаходяться теоретично (обчисленням):

,

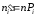де n – кількість спостережень;

Р_i – ймовірність значення 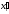ознаки, що спостерігається, за умови, щоХ має визначений розподіл.

В нашому випадку величина Х (генеральна сукупність) розподілена нормально, тому вирівнюючі частоти знаходять за формулою:

,

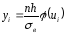де n – кількість випробувань (обсяг вибірки);

h – довжина часткового інтервалу;

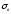–вибіркове середнє квадратичне відхилення;

;

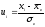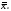вибіркове середнє;

х_і – середина і-го часткового інтервалу;

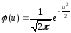
Значення функції 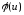наведені в додатку 3.

Внаслідок групування ознак х_і неперервної випадкової величини Х і переходу від інтервального варіаційного ряду до дискретного, отриманий такий розподіл для множини Х, зображений в таблиці (табл.9):

Таблиця 9

Частковий інтервал, Хі	Сума частот варіант інтервалу, ni
-1,447	7
-0,853	9
-0,258	11
0,336	13
0,930	7
2,119	3

Вибіркове середнє 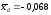, вибіркове середнє квадратичне відхилення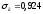

Обчислимо вирівнюючі частоти за формулою 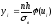, для чого складемо розрахункову табл. 10.

Таблиця 10

xi	ni
-1,447	7	-1,379	-1,492	0,1315	4,229
-0,853	9	-0,785	-0,849	0,2803	9,014
-0,258	11	-0,190	-0,206	0,391	12,573
0,336	13	0,404	0,437	0,3637	11,696
0,930	7	0,999	1,080	0,2227	7,161
2,119	3	2,187	2,367	0,0246	0,791
	50				45,464

За отриманими даними будуємо нормальну (теоретичну) криву за вирівнюючими частотами і полігон частот, що зображені на рис. 3.

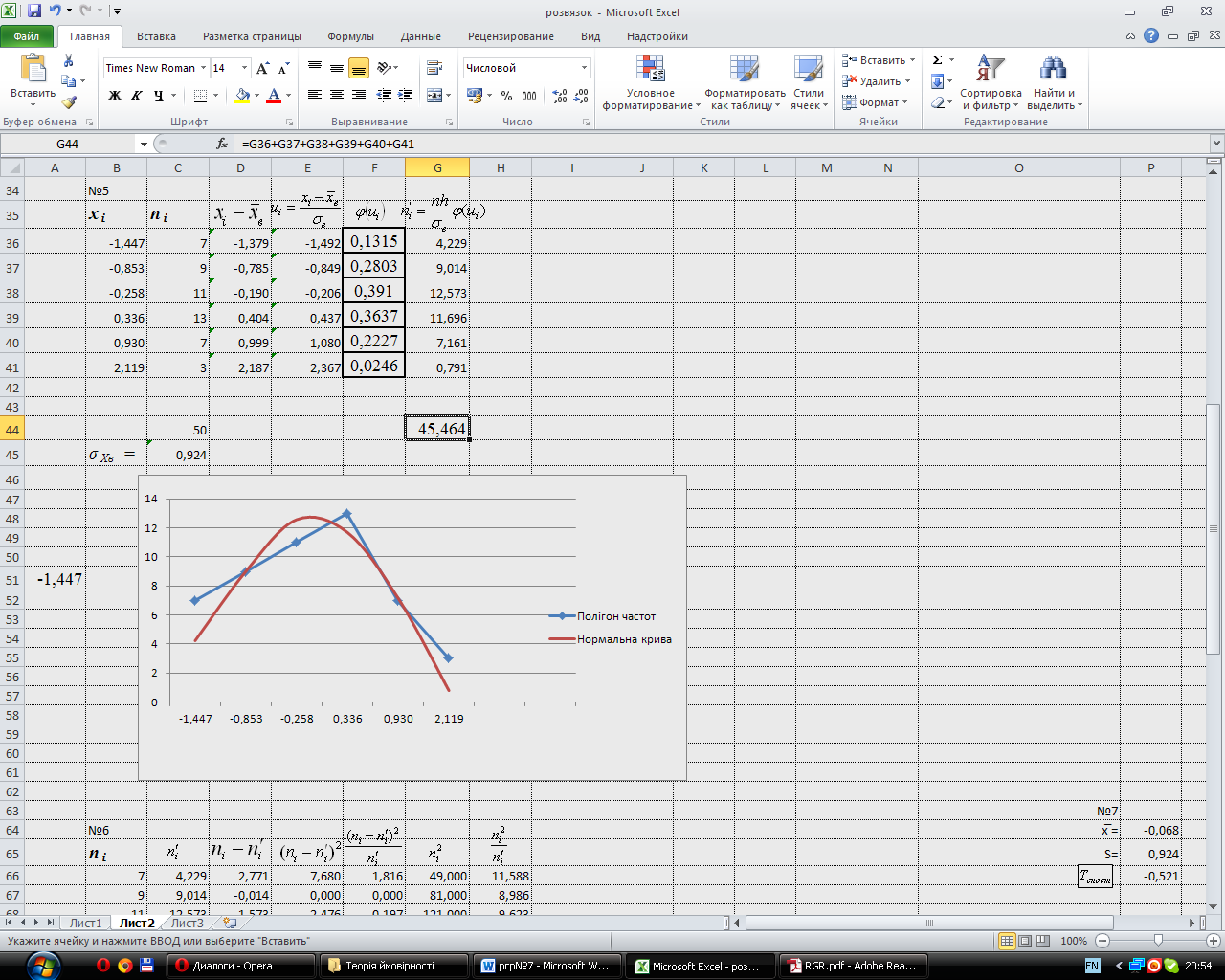
Рис. 3

Для множини Y запишемо емпіричний розподіл в табл. 11.

Таблиця 11

yi	ni
-1,695	6
-1,063	8
-0,431	10
0,201	10
0,833	8
1,465	5
2,413	3

Нагадаємо, що вибіркове середнє множини Y 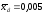, а вибіркове середнє квадратичне відхилення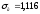

Обчислимо вирівнюючі частоти (табл. 12).

Таблиця 12

yi	ni
-1,695	6	-1,700	-1,523	0,1257	3,559
-1,063	8	-1,068	-0,957	0,2541	7,194
-0,431	10	-0,436	-0,391	0,3697	10,467
0,201	10	0,196	0,176	0,3932	11,132
0,833	8	0,828	0,742	0,3034	8,590
1,465	5	1,460	1,308	0,1714	4,853
2,413	3	2,408	2,157	0,0396	1,121
	n = 50				46,916

Нормальна крива за вирівнюючими частотами і полігон частот для множини Y зображена на рис. 4.

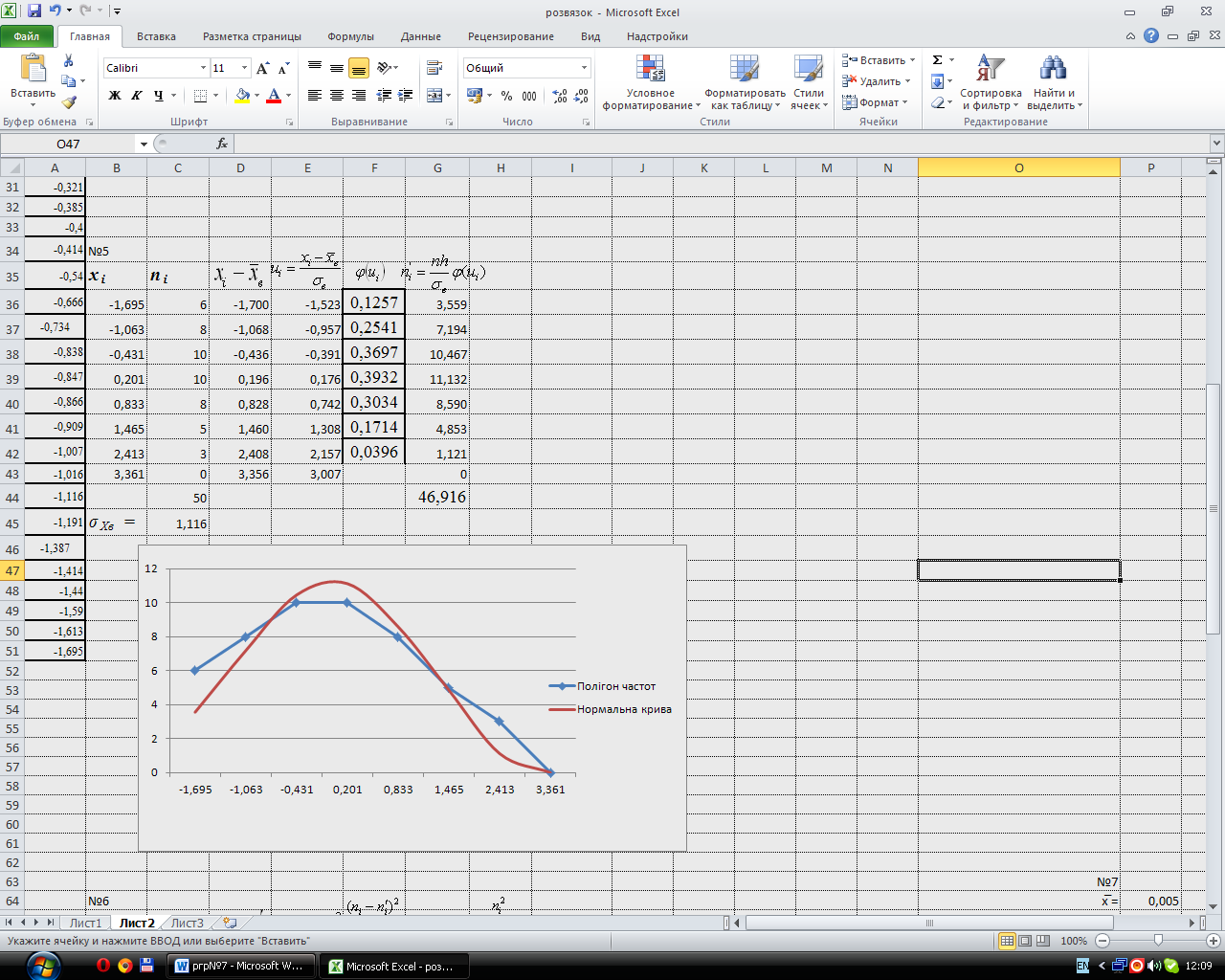
Рис. 4

Порівняння графіків наочно показує, що побудована теоретична крива задовільно відображає результати спостережень.