1. 210-7 Дж. Б) 210-5 Дж. В) 210-3 Дж. Г) 210-4 Дж. Д) 210-6 Дж.

101. Конденсатор ємністю С=100 мкФ заряджається до напругиU=500 В заt=0,5 с. Визначтесереднєзначення зарядного струмуІ_сер.

А) 50 мА. Б) 10 мА. В) 200 мА. Г) 20 мА. Д) 100 мА.

101. Як змінюється електрична ємність провідника при наближенні до нього іншо-

го незарядженогопровідника ?

А) Збільшується. Б) Зменшується. В) Не змінюється.

Г) Зменшується тільки при русі. Д) Збільшується тільки при русі.

101. Плоский повітряний конденсатор із площею пластин S=50 см² і відстанню між ними d=2 мм заряджається від батареї з напругою U=500 В. Визначите величину за-рядуqна пластинах конденсатора.

А) 2,410^-10 Ф. Б) 7,210^-7 Ф. В) 5,410^-9 Ф. Г) 1,110^-8 Ф. Д) 3,610^-6 Ф.

101. Визначите напруженість поля Eу конденсаторі за умов попередньої задачі.

А) 50 кВ/м. Б) 250 кВ/м. В) 100 кВ/м. Г) 200 кВ/м. Д) 150 кВ/м.

101. Знайти різницю потенціалів Uміж пластинами конденсатора, ємністюC=100 мкФ, який має заряд на пластинахq=510^-3Кл.

А) 25 В. Б) 5 В. В) 50 В. Г) 100 В. Д) 75 В.

101. У скільки разів зміниться ємність плоского конденсатора, якщо робочу повер-хню його пластин S зменшитиу 2 рази, а відстань між нимиdзбільшитиу 3 рази ?

А) Зменшиться у 1,5 рази. Б) Збільшиться у 6 разів. В) Зменшиться у 0,7 рази.

Г) Збільшиться у 1,5 рази. Д) Зменшиться у 6 разів.

101. У скільки разів зміниться ємність плоского конденсатора, якщо робочу повер-хню його пластин Sзбільшитиу 3 рази, а відстань між нимиdзменшитиу 2 рази ?

А) Збільшиться у 6 разів. Б) Зменшиться у 1,5 рази. В) Збільшиться у 1,5 рази.

Г) Збільшиться у 0,7 рази. Д) Зменшиться у 6 разів.

101. Два конденсатори ємностями C₁=4 мкФ таC₂=1 мкФ з'єднаніпослідовно. Ви-значте загальну ємність цієї батареї конденсаторів.

А) 0,4 мкФ. Б) 2,5 мкФ. В) 0,8 мкФ. Г) 5,0 мкФ. Д) 1,2 мкФ.

101. Два конденсатори ємностями C₁=0,25 мкФ таC₂=0,5 мкФ з’єдналипослідовно. Визначте ємність утвореної батареї конденсаторів.

А) 0,75 мкФ. Б) 0,17 мкФ. В) 11 мкФ. Г) 1,4 мкФ. Д) 0,51 мкФ.

101. Конденсатор ємністю С₁=20 мкФ, заряджений до напругиU₁=100 В, з'єдналипаралельноіз конденсатором невідомої ємностіC₂, зарядженого до напругиU₂=40 В. Після з'єднання їх обкладинок із однаковими зарядами установилась напругаU= =80 В. Визначте ємність невідомого конденсатора.

А) 20 мкФ. Б) 5 мкФ. В) 40 мкФ. Г) 10 мкФ. Д) 50 мкФ.

101. Заряд конденсатора qдорівнює 410^-4Кл, а напруга між його обкладинкамиU= =500 В. Визначте енергіюWелектричного поля у конденсаторі.

А) 250 мДж. Б) 50 мДж. В) 100 мДж. Г) 200 мДж. Д) 150 мДж.

101. Визначте енергію електричного поля конденсатора, ємністю С=50 мкф, якщо різниця потенціалівUміж його пластинами дорівнює 100 В.

А) 250 мДж. Б) 50 мДж. В) 400 мДж. Г) 25 мДж. Д) 150 мДж.

101. Конденсатор ємністю С=0,25 мкФ з’єднали з джерелом напругиU=3 В. Визна-чте енергію зарядженого конденсатораW.

А) 110 мкДж. Б) 1,1 мкДж. В) 1100 мкДж. Г) 11 мкДж. Д) 0,11 мкДж.

101. Лампа фотоспалаху живиться від конденсатора ємністю С=800 мкФ, зарядже-ного до напругиU=300 В. Визначтесередню потужністьP_серспалаху лампи, якщо він триває=2,4 мс.

А) 5,0 кВт. Б) 2,5 кВт. В) 15 кВт. Г) 1,5 кВт. Д) 7,5 кВт.

101. Яка кількість теплоти виділиться у провіднику при розряді через нього кон-денса-тора ємністю С=50 мкф, зарядженого до різниці потенціалівU=120 В ?

А) 540мДж. Б) 180 мДж. В) 360 мДж. Г) 240 мДж. Д) 720 мДж.

101. Плоский горизонтальний конденсатор з відстанню між пластинами d=4 мм за-нуренийдо половиниу гас, діелектрична проникність якого=2,1. На скільки по-трібно розсунути пластини конденсатораd, щоб його ємністьлишилась незмін-ною?

А) 1,5 мм. Б) 2,0 мм. В) 0,5 мм. Г) 1,0 мм. Д) 2,5 мм.

101. Різниця потенціалів між пластинами конденсатора U=90 В. Площа кожної пла-стиниS=60 см², а зарядq=10^-9Кл. Визначте відстань між пластинамиd.

А) 1,2 мм. Б) 4,8 мм. В) 2,4 мм. Г) 6,0 мм. Д) 3,6 мм.

101. Знайти різницю потенціалів Uміж пластинами повітряного конденсатора, що має заряд на пластинахq=2 мКл і електричну ємністьC=200 мкф.

А) 20 В. Б) 5 В. В) 10 В. Г) 25 В. Д) 15 В.

101. Плоский повітряний конденсатор із площею пластин Sпідключений до джере-ла струму з EРС, рівноюE. Визначте роботу зовнішніх силAпри розсуванні плас-тин від відстаніd₁до відстаніd₂, якщо пластини перед розсуваннямвідключиливід джерела струму.

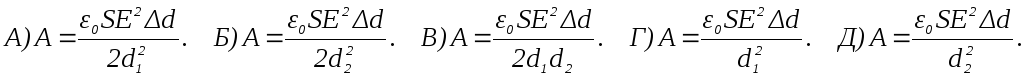
101. Конденсатор ємністю C₁, заряджений до різниці потенціалівU₁,після відклю-ченнявід джерела струму був з'єднаний з незарядженим конденсатором ємністюC₂. Визначите енергіюW, що виділиться при утворенні іскри у момент з'єднання конденсаторів.

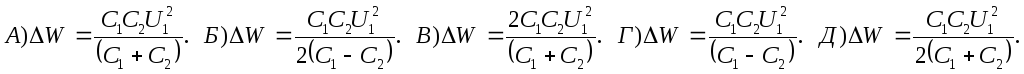
101. Визначте електричну ємність Сплоского повітряного конденсатора, площа об-кладинок якогоS=100 см², а відстань між нимиd=0,1 мм.

А) 221 пФ. Б) 885 пФ. В) 116 пФ. Г) 442 пФ. Д) 694 пФ.

101. Плоский повітряний конденсатор зарядили і відключиливід джерела струму. Як зміниться енергія конденсатора призменшеннівідстані між пластинами у 2 ра-зи ?

А) Зменшиться у 4 рази. Б) Збільшиться у 4 рази. В) Зменшиться у 2 рази.

Г) Збільшиться у 2 рази. Д) Зменшиться у разів.

101. Маленька кулька, що має заряд q=16,7^.10^-9Кл, торкнуласявнутрішньої повер-хніпорожнистої незарядженої великої кулі радіусомR=20 см. Знайти поверхневу густину електричного зарядувеликої кулі.

А) 228 нКл/м². Б) 17 нКл/м². В) 154 нКл/м². Г) 33 нКл/м². Д) 86 нКл/м².

101. Знайти поверхневу густину електричного заряду назовнішній поверхніпо-рожнистої металевої кулі радіусомR=20 см, якщо в її центрі розміщена заряджена кулька, що має зарядq=+3,2^.10^-9Кл.

А) 1,6 мкКл/м². Б) 12,8 мкКл/м². В) 3,2 мкКл/м². Г) 9,6 мкКл/м². Д) 6,4 мкКл/м².

101. Визначите кількість зайвих електронів Nна зарядженій порошинці вагоюР= =510^-11Н, якщо вона врівноважується у полі плоского конденсатора, напруга між пластинами якогоU=3 кВ, а відстань між нимиd=2 см. (е=1,610^-19Кл).

А) 520. Б) 2080. В) 260. Г) 1040. Д) 4160.

101. Конденсатор, який складається із двох паралельних пластин, має ємність С=5 пФ. Який заряд має кожна з його обкладинок, якщо різниця потенціалів між нимиφ=100 В ?

А) 0,5 нКл. Б) 5,0 мкКл. В) 5,0 нКл. Г) 0,5 мкКл. Д) 50 нКл.

101. Маленька кулька підвішена на тонкій невагомій шовковій нитці між круглими горизонтальними пластинами плоского повітряного конденсатора, радіус яких R= =10 см. Кулька має зарядq=-3,3·10^-9Kл. Koли пластинам конденсатора надали за-рядQ=327·10^-9Kл, сила натягу нитки збільшилась вдвічі. Визначте масуmкульки.

А) 0,2 г. Б) 0,8 г. В) 0,1 г. Г) 1,6 г. Д) 0,4 г.

101. Плоский конденсатор зарядили за допомогою джерела з напругою U=200 В. Потім конденсаторвід'єдналивід джерела. Якою стане напруга між пластинами, якщо відстань між ними збільшити відd₁=0,2 мм доd₂=0,7 мм, a простір між плас-тинами заповнити слюдою ? Діелектрична проникність слюдиε=7.

А) 75 В. Б) 125 В. В) 100 В. Г) 150 В. Д) 50 В.

101. Визначити величину заряду q, який треба надати двомпаралельноз'єднаним конденсаторам, щоб зарядити їх до різниці потенціалівU=20 кВ, якщо ємності конденсаторівС₁=2 нФ таС₂=11 нФ.

А) 650 мкКл. Б) 260 мкКл. В) 320 мкКл. Г) 130 мкКл. Д) 390 мкКл.

101. Надавши провіднику заряд q=2^.10^-2Кл, його зарядили до потенціалуφ=100 В. Визначити електроємність провідника.

А) 150 мкФ. Б) 300 мкФ. В) 100 мкФ. Г) 200 мкФ. Д) 250 мкФ.

101. Який заряд qміститься на кожній із пластин конденсатора, якщо різниця по-тенціалів між обкладинкамиU=200 В, а ємність конденсатораС=0,5 мкФ ?

А) 0,5 мКл. Б) 2,0 мКл. В) 0,1 мКл. Г) 1,0 мКл. Д) 0,2 мКл.

101. Визначити ємність конденсатора, який має заряд q=2·10^-3Кл і різницю потен-ціалів між пластинамиU=10 В. Відповідь надати у мікрофарадах.

А) 200 мкФ. Б) 50 мкФ. В) 150 мкФ. Г) 100 мкФ. Д) 250 мкФ.

101. Визначити енергію електричного поля конденсатора, який має заряд q=50 мкФ і різницю потенціалів між пластинамиU=100 В.

А) 1,5 мДж. Б) 5,0 мДж. В) 1,0 мДж. Г) 0,5 мДж. Д) 2,5 мДж.

101. Заряд конденсатора q=4·10^-4Кл, а напруга на обкладинкахU=500 В. Визначи-ти енергіюWцього конденсатора.

А) 250 мДж. Б) 150 мДж. В) 200 мДж. Г) 100 мДж. Д) 50 мДж.

101. У скільки разів зміниться ємність конденсатора, якщо робочу площу його пла-стин Sзменшитиу 2 рази, а відстань між нимиdзменшитиу 3 рази ?

А) Зменшиться у 6 разів. Б) Збільшиться у 1,5 рази. В) Зменшиться у 1,5 рази.

Г) Збільшиться у 0,67 разів. Д) Збільшиться у 6 разів.

101. Плоский повітряний конденсатор зарядили. Як зміниться напруженість елект-ричного поля між його пластинами, якщо відстань між ними збільшитиу 2 рази ?

А) Збільшиться у 4 рази. Б) Збільшиться у разів. В) Зменшиться у 2 рази.

Г) Зменшиться у 4 рази. Д) Збільшиться у 2 рази.

101. Плоский повітряний конденсатор зарядили і відключиливід джерела струму. Як зміниться енергія конденсатора призменшеннівідстані між його пластинамиdу 2 рази ?

А) Зменшиться у 2 рази. Б) Збільшиться у 4 рази. В) Зменшиться у разів.

Г) Зменшиться у 4 рази. Д) Збільшиться у 2 рази.

101. Визначити роботу, яку виконує електричне поле при щільному наближенні пластин плоского конденсатора, якщо заряд конденсатора дорівнює q=2,5·10^-4Кл, а різниця потенціалів між обкладинками конденсатораU=40 В.

А) 0,5 мДж. Б) 25 мДж. В) 2,5 мДж. Г) 5,0 мДж. Д) 50 мДж.

101. Повітряний конденсатор, заряджений до різниці потенціалів U₀=800 В, з'єдну-ютьпаралельноз однаковим за розмірами незарядженим конденсатором, який за-повнений діелектриком. Яка діелектрична проникністьεдіелектрика, якщо після цього з'єднання різниця потенціалів між пластинами обох конденсаторів сталаU= =100 В ?

А) =5. Б) =7. В) =2. Г) =4. Д) =3.

101. Електрична схема, що складається з двох послідовноз'єднаних конденсаторів, ємностямиС₁=1 мкФ таС₂=3 мкФ приєднали до джерела постійної напругиU= =220 В. Визначте напругу на кожному конденсаторіU₁таU₂

А) 155 і 65 В. Б) 135 і 85 В. В) 175 і 45 В. Г) 145 і 75 В. Д) 165 і 55 В.

101. Конденсатору ємністю С=2 мкФ надали зарядq=10^-3Кл. Обкладинки конден-сатора з'єднали провідником. Знайти кількість теплотиQ, що виділиться у провід-нику під час розрядження.

А) 500 мДж. Б) 150 мДж. В) 250 мДж. Г) 50 мДж. Д) 350 мДж.

101. Визначити сумарну електроємність батареї конденсаторів, ємностямиС₁=2мкФ,С₂=4 мкФ, С₃=6 мкФ,С₄=3 мкФ,С₅=4 мкФ,С₆=5 мкФ,С₇=6 мкФ, якщо вони з'єднанийпослідовно.

А) 10 мкФ. Б) 0,5 мкФ. В) 1,0 мкФ. Г) 20 мкФ. Д) 5,0 мкФ.

101. На конденсаторі, увімкненому до ідеального коливального контуру, ефектив-нанапруга дорівнює 100 В. Ємність конденсатораС=10 пФ. Визначитимакси-мальнезначення електричної енергіїW_елу контурі.

А) 98 мДж. Б) 24 мДж. В) 155 мДж. Г) 49 мДж. Д) 196 мДж.

101. Ємність змінного конденсатора у приймачі змінюється в межах від С₁доС₂= =9С₁. Визначити діапазон довжин хвиль, які приймає контур приймача, якщо ємністьС₁відповідає довжині хвиліλ₁=3 м.

А) =4 м. Б) =12 м. В) =3 м. Г) =9 м. Д) =6 м.

101. У вертикальне електричне поле між пластинами плоского конденсатора вмі-щено крапельку олії, заряджену одним електроном. Напруженість електричного поля підібрано так, що крапелька перебуває у стані рівноваги. Визначити радіус крапельки, якщо різниця потенціалів між пластинами конденсатора U=500 В, від-стань між пластинамиd=0,5 см, густина оліїρ=0,9 г/см³. (е=1,6·10^-19Кл).

А) 3,810^-6 м. Б) 9,710^-3 м. В) 2,410^-4 м. Г) 7,610^-7 м. Д) 1,910^-5 м.

101. Дві металеві кульки радіусами R₁іR₂розташовані так, що відстань між ними набагато більша від їх радіусів. На кулю радіусомR₁подано зарядQ. Які заряди будуть містити обидві кульки після з'єднання їх провідником ? Вважати, що тон-кий провідник, яким з'єднують кульки, має нехтовно малу ємність.

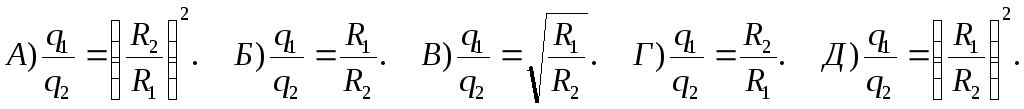
101. Пластини плоского конденсатора ізольовані одна від одної шаром діелектрика

з діелектричною проникністю ε=3. Конденсатор заряджений до різниці потенціалівU₀=1 кВ іроз'єднанийіз джерелом напруги. Визначити різницю потенціалів між пластинами конденсатораUпісля видалення діелектрика.

А) 6,0 кВ. Б) 1,5 кВ. В) 3,0 кВ. Г) 0,5 кВ. Д) 4,5 кВ.

101. До конденсатора ємністю С₁=2 мкФпаралельноприєднали незаряджений кон-денсатор ємністюС₂. Визначте ємністьC₂, якщо енергіяWелектричного поля бата-реї після їх з'єднання зменшилась у 3 рази.

А) 6 мкФ. Б) 3 мкФ. В) 8 мкФ. Г) 1 мкФ. Д) 4 мкФ.

101. У плоский конденсатор влітає електрон зі швидкістю V=2·10⁷м/с, спрямова-ною паралельно пластинам конденсатора. На яку відстаньhвід свого початкового напрямку зміститься електрон, пролетівши конденсатор, якщо відстань між плас-тинамиd=2 см, довжина конденсатораl=5 см, а різниця потенціалів між пластина-миU=200 В ? Питомий заряд електронаe/m=1,76·10¹¹Кл/кг.

А) 5,5 мм. Б) 9,4 мм. В) 3,2 мм. Г) 7,6 мм. Д) 2,7 мм.

101. Конденсатор ємністю С₁=3 мкФ заряджений до різниці потенціалівU₁=40 В. Після відключення від джерела струму, його приєднали до другого незарядженого конденсатора ємністюС₂=5 мкФ. Визначити енергіюW, яка виділиться при утворенні іскри в момент з'єднання конденсаторів.

А) 4,5 мДж. Б) 1,5 мДж. В) 7,5 мДж. Г) 2,5 мДж. Д) 0,5 мДж.

101. Заряд конденсатора становить 400 мкКл, а напруга між його обкладками U= =500 В. Визначте енергіюWелектричного поля цього конденсатора.

А) 0,1 Дж. Б) 1,0 Дж. В) 10 Дж. Г) 100 Дж. Д) 0,01 Дж.

101. Визначте потенціал  кулі радіусомR=3 см, якщо їй надати електричний зарядq=10 нКл.

А) 0,5 кВ. Б) 6,0 кВ. В) 3,0 кВ. Г) 1,5 кВ. Д) 2,5 кВ.

101. Маленька металева кулька масою m=1 г, якій надали зарядq=10^-7Кл, кинута здалеку зі швидкістюV=1 м/с у металеву сферу із зарядомQ=310^-7Кл. При якомунайменшомузначенні радіуса сфериR_minкулька досягне її поверхні ?

А) 72 см. Б) 27 см. В) 96 см. Г) 13 см. Д) 54 см.

101. Між вертикальними пластинами конденсатора, що лежать на відстані d=1 см одна від одної, висить на нитці заряджена кулька масоюm=0,1 г. Після того, як на пластини була подана напругаU=1 кВ, нитка з кулькою відхилилася на кут=10⁰. Визначте заряд кулькиq.

А) 3,4 нКл. Б) 0,9 нКл. В) 5,1 нКл. Г) 1,7 нКл. Д) 6,8 нКл.

ОСНОВИ ТЕОРІЇ З РОЗДІЛУ “ЗАКОНИ ПОСТІЙНОГО СТРУМУ”

Електричним струмом називається упорядкований (спрямований) рух електричних зарядів. За напрямок струму умовно приймають напрямок руху позитивних зарядів. Струм може існувати і у твердих тілах, і у рідинах, і у газах, і у вакуумі. Розрізняють струм провідності та конвекційний струм. До струму провідності відноситься упорядкований рух в речовині або у вакуумі вільних заряджених частинок – носіїв струму. Це є дрейфовий рух електронів у провідниках, іонів у електролітах, електронів та дірок у напівпровідниках, іонів та електронів у газах, а також пучок електронів у вакуумі. Конвекційний струм – це упорядкований рух електричних зарядів, здійснюване переміщенням у просторі зарядженого макроскопічного тіла. Для виникнення та існування електричного струму необхідно, з одного боку, наявність вільних носіїв струму, здатних переміщуватись упорядковано, а з іншого боку – наявність електричного поля, енергія якого витрачалася б на їх упорядкований рух. Постійним називається електричний струм, величина і напрямок якого не змінюються зі спливом часу.

Кількісними характеристиками електричного струму є сила струму I та густи-на струму j. Сила струму – скалярна фізична величина, визначувана електричним зарядом, проходячому через поперечний перетин провідника за одиницю часу:

Основна одиниця сили струму – Ампер – сила постійного стру-му, який проходячи по двох нескінченних паралельних прямо-лінійних провідниках нескінчено малого поперечного перерізу,

розташованих у вакуумі на відстані 1 м один від одного, створює між цими провід-никами силу взаємодії, рівну 210^-7 Н на кожен метр довжини. Для постійного стру-му I=q/t.

Густина струму – векторна фізична величина, модуль якої визначається си-лою струму, що проходить через одиницю площі поперечного перетину провідника,

перпендикулярного напрямку струму: Одиниця густини струму – Ампер на квадратний метр (А/м2). Гус-тина струму характеризує розподіл електричного струму по перері-

зу провідника. Якщо концентрація вільних носіїв струму у провіднику дорівнює n, а елементарний заряд носія e, то за час dt через поперечний переріз S провідника переноситься заряд dq=neV_cеpSdt, де V_cеp – середня швидкість дрейфу носіїв струму. При цьому сила струму I=dq/dt=neV_cеpS, а густина струму j=I/S=neV_cеp. Густина струму j – вектор, сппрямований уздовж напрямку струму (співпадає з напрямком упорядкованого руху позитивних носіїв струму). Густина струму у провіднику дорі-

внює: де me – маса електрона, Ucеp - середня швидкість тепло-вого руху,  - довжина вільного пробігу електрона.

Коефіцієнт при напруженості поля визначається властивостями матеріалу провідни-ка і називається його питомою провідністю. Позначивши її через , одержаний ви

раз можна переписати у вигляді: Це співвідношення, яке зв'язує густину струму у будь-якій точці про-

відника із напруженістю електричного поля у цій крапці, називається законом Ома у диференціальній формі. Очевидно, що напрямки векторів j та E співпадають, ос-кільки носії заряду у кожній крапці рухаються у напрямку поля. Закон Ома справедливий і для змінних електричних полів. Величина, обернена електричній провідності, позначається  і називається питомим опором провідника (=1/).

Кінетична енергія дрейфу електронів передається кристалічним гратам провід-ника і перетворюється на тепло. Середнє число зіткнень електрона за 1 секунду із вузлами кристалічної решітки z_cеp=/U_cеp. Якщо n – концентрація електронів, то енергія, передавана решітці у одиниці об'єму провідника за одиницю часу визначається

формулою: де  - питома провідність матеріалу провідника. Це співвідношення було вперше експериментально вста-

новлено англійським фізиком Джоулем і незалежно від нього, російським фізиком Ленцем, і носить назву закону Джоуля-Ленца у диференціальній формі. Ліва частина цієї формули  є кількістю тепла, що виділяється у одиниці об'єму провідника за одиницю часу при протіканні по ньому електричного струму, називається питомою тепловою потужністю струму = =dQ/dVdt [Дж/м³с]=[Вт/м³].

Провідники (метали) володіють як великою електропровідністю, так і високою теплопровідністю. Це пояснюється тим, що носіями струму і теплоти у металах є ті ж самі частинки – вільні електрони. Переміщаюючись у металі, вони переносять не лише електричний заряд, а і властиву їм енергію теплового руху, тобто здійснюють перенесення теплоти. Вимірювання показали, що майже для всіх металів відношен-ня коефіцієнта теплопровідності  до питомої провідності  при однаковій темпера-

де	турі однакове і збільшується пропорційно їй: Тут k– стала Больцмана, е – заряд електрона. Це твер- дження має назву закону Відемана-Франца.

Одержимо вирази законів Ома і Джоуля-Ленца у загальнішому, інтегральному вигляді. Для цього закон у диференціальному вигляді j=E перепишемо, з урахуван-ням того, що для постійного струму j=I/S, =1/. Тоді, для напруженості поля має-мо: E=I/S. Помножимо обидві частини рівності на елемент довжини провідника dl

	та проінтегруємо по усій його довжині: Ліва частина цієї рівності є різницею потенциалів (напруга) на кінцях провідника. Тоді одержану рівність можна переписати:
де		називається електричним опором провідника, який характеризує міру протидії провідника про-тіканню у ньому електричного струму. Одержане

співвідношення найчастіше записується у вигляді I=U/R, і носить назву закону Ома для однорідної ділянки кола (що не містить джерела струму,) формулюється так: си-ла струму у провіднику прямо пропорційна прикладеній напрузі і обернено пропорційна опору провідника.

Якщо провідник складається із однорідного матеріалу (=const) і має однако-вий поперечний переріз (S=const), то залежність електричного опору від його геоме-

тричних розмірів має вигляд: Розмірності електричного опору R]=[Ом], питомого опору []= [Омм], електричної провідності []=[1/R]=[См]=[1/Ом] (сименс), питомої про-

відності []=[1/]=[1/Омм]=[См/м].

При послідовному з'єднанні декількох провідників (I₁=I₂=…=I_n), загальний опір всієї ділянки кола визначається співвідношенням: R_заг=R₁+R₂+…+R_n. При пара-

лельному з'єднанні (U1=U2=…=Un) загальний опір усієї ді-лянки кола знаходять із формули:

При підвищенні температури зростає інтенсивність теплового руху іонів кристалічної решітки, і частішають зіткнення дрейфуючих електронів з іонами, тому опір провідників залежить від температури. Залежності питомого опору (і опору) провідників від температури мають вигляд:

де  і 0, R і R0 – відповідно питомі опори та опори провідника при температурах t0C і 00С,  - темпера-

турний коефіцієнт опору провідника. Значення  при різних температурах змінюються, проте для всіх чистих металів при не дуже низьких температурах =1/273 К^-1.

Закон Джоуля-Ленца у диференціальній формі =E² може бути представле-ний у вигляді:

звідки

Тут враховано, що R=dl/dS - електричний опір провідни-

ка, а dV=dSdl – його елементарний об'єм. Застосувавши закон Ома для однорідної ділянки кола, можна записати цей закон у іншому вигляді:

	Це - закон Джоуля-Ленца у інтегральному вигляді, що встановлює кількість виділеної у провіднику теплоти
	при протіканні у ньому електричного струму. Якщо сила струму змінюється у часі, кількість теплоти, що виділилась, визначається інтегруванням:

Якщо у колі на носії струму (які передбачаються позитивними) діють тільки сили електростатичного поля, то вони переміщаються від точок із великим потенціалом до точок із меншим потенціалом. Це приводить до вирівнювання потенціалів в усіх точках кола і до зникнення електростатичного поля. Тому, для існування постійного струму на ділянці кола, до його кінців потрібно підключити пристрій, який вироблятиме розподіл різнойменних зарядів. Такі пристрої називаються джерелами струму. Усередині джерел струму електричні заряди повинні рухатись у напрямку, протилежному дії сил електричного поля. Таке переміщення можливе тільки за рахунок сторонніх сил – сил неелектростатичного походження, які діють на заряди з боку джерела струму. Наприклад, у гальванічних елементах вони виникають за рахунок енергії хімічних реакцій між електродами і електролітами, у генераторах – за рахунок механічної енергії обертання ротора генератора і таке інше. Роль джерела струму у електричному колі така ж сама, як роль насосу, необхідного для перекачування рідини у гідравлічній системі. Завдяки дії сторонніх сил усередині джерела струму, на його полюсах підтримується постійна різниця потенціалів, а у підключеному до них електричному колі тече постійний електричний струм.

При переміщенні зарядів усередині джерела струму витрачається енергія, а от-же, сторонні сили здійснюють роботу. Фізична величина, визначувана роботою сторонніх сил по переміщенню одиничного позитивного заряду, називається елект-рорушійною силою (ЕРС) джерела струму: =А_стор/q. Розмірність ЕРС – Вольт: [1 Дж/Кл]=[1 B]. Окрім ЕРС, джерело струму характеризується внутрішнім опором r, що характеризує міру протидії самого джерела протіканню у ньому електричного струму. Розглянувши протікання струму по неоднорідній ділянці кола (яка містить джерело струму) і застосувавши закон збереження і перетворення енергії, нескладно

одержати вираз: Це співвідношення носить назву закону Ома для неоднорідної ді-лянки кола (узагальненого закону Ома). Тут (1-2) – різниця по-

тенціалів, прикладена до кінців ділянки кола,  - сумарна ЕРС усіх джерел струму, включених в дану ділянку. Як і сила струму,  - скалярна величина: 0, якщо ЕРС джерела сприяє руху позитивних зарядів, і 0 – якщо ЕРС перешкоджає їх руху. Проаналізуємо цей закон для декількох окремих випадків.

1. Якщо ділянка кола однорідна (не містить ЕРС, тобто =0), то закон набуває вигляду: I=/R=U/R – що співпадає із одержаним раніше виразом. Очевидно, що напруга на кінцях ділянки кола дорівнює різниці потенціалів тільки у тому випадку, якщо на ділянці відсутнє джерело струму.

2. Якщо коло замкнуте, то ₁=₂, то закон набуває вигляду: I=/R, де R – повний опір ділянки кола, включаючи внутрішній опір джерела струму r (R=R_зовн+r_внут).

3. Якщо коло розімкнене, то I=0, тоді = - ЕРС у розімкненому колі дорівнює різниці потенціалів на його кінцях, тобто виміряти ЕРС можна на клемах розім-кненого джерела струму.

Якщо до ділянки кола постійного струму прикладена напруга U, то за проміжок часу dt через поперечний переріз провідника переноситься заряд dq=Idt, при цьому силами електростатичного поля здійснюється робота dA=Udq=IUdt. Ця робота може піти, наприклад, на збільшення внутрішньої енергії провідника (на його нагрівання), на рух провідника у магнітному полі і таке інше. Повна робота, здійс-

нювана джерелом струму, ЕРС якого дорівнює , визначається так: Фізична величина, що характеризує бистроту здійснення роботи і

визначувана роботою за одиницю часу, називається електричною потужністю.

	Потужність, що розвивається джерелом струму на ділянці кола: Одиниця потужності – Ват [P]=1 [Дж/с]=[1 АВ]=[1 Вт]. При цьо-му потужність, що виділяється у зовнішньому колі (корисна поту-
		жність) дорівнює: Фізична величина, що характеризує, яка частина повної потуж- ності джерела струму може бути використана у зовнішній час-
			тині кола, називається коеффіцієнтом корисної дії джерела струму , який може бути розрахований із співвідношення:

де R – опір зовнішньої ділянки кола, r – внутрішній опір джерела струму.

Рідини, як і тверді тіла, можуть бути діелектриками і провідниками. До числа діелектриків відноситься дистильована вода, а до провідників відносяться електроліти – розчини кислот, лугів, солей, які при проходженні через них струму, хімічно розпадаються. Заряди у електролітах переносяться іонами. Якщо судину із розчином електроліту включити у електричне коло, то негативні іони (аніони) почнуть ру-хатись до аноду (позитивного електроду), а позитивні іони (катіони) – до катоду (негативного електроду). Оскільки електричний струм у електролітах обумовлений рухом іонів, така провідність називається іонною. Закон Ома для електролітів має ви-

гляд: де  - провідність електроліту, b+ і b- - рухливості відповідно катіонів і аніонів, які характеризують швидкості їх руху, q –

заряд іона, n – концентрація іонів. Слід зазначити, що провідність електролітів у багато разів менша, ніж у металів, і значно підвищується при збільшенні температури.

При такій провідності протікання струму пов'язане з перенесенням речовини. На електродах відбувається виділення речовин, які входять до складу електролітів. Процес виділення на електродах речовин, зв'язаний із окислювально-відновлюваль-ними реакціями, називається електролізом. В результаті електролізу відбувається накопичення поблизу електродів продуктів хімічного розпаду електролітів.

Вивчаючи явища, які відбуваються при протіканні струму через електроліти, англійський фізик М.Фарадей експериментально встановив два основні закони електролізу. Перший закон Фарадея: маса речовини, що виділилась при електролізі на будь-якому з електродів, прямопропорційна кількості електрики, що пройшла через

m=Kq,

електроліт: де коефіцієнт K називається електрохімічним еквівалентом речовини,

який дорівнює масі даної речовини, що виділиться на електроді при проходженні через електроліт заряду у 1 Кулон. Якщо струм постійний, то q=It, тоді m=KIt.

Другий закон Фарадея: Електрохімічні еквіваленти різних речовин пропорцій-

ні їх хімічним еквівалентам: де 1/F – коефіцієнт пропорційності, однаковий для всіх речовин. Вели-чина F=9,65104 Кл/моль знайдена із досвіду, має назву сталої Фара-

дея і дорівнює добутку елементарного заряду на число Авогадро F=eN_A. Відношення молярної маси речовини до її валентності М/n називають хімічним еквівалентом речовини. Обидва закони Фарадея можна об'єднати, підставивши значення K у пер-

ший закон: Знаючи число Авогадро і сталу Фарадея, вперше у 1874 році було отримане значення елементарного електричного заряду

е=1,610^-19 Кл.

Газ стає провідником електрики, якщо деяка частина його молекул іонізується – тобто відбудеться розщеплювання нейтральних молекул газу на іони і вільні електрони. Для цього потрібно піддати газ дії іонізатора. Іонізацією газів називається процес розщеплювання нейтральних молекул газу на іони і вільні електрони. Можливими іонізаторами є:

1) Сильний нагрів – зіткнення швидких молекул стають настільки сильними, що відбувається їх розщеплювання на іони;

2) Короткохвильове електромагнітне випромінювання – ультрафіолетове, рентгенівське або –випромінювання.

3) Опромінювання потоками заряджених частинок – електронів, протонів, -частинок і таке інше.

Енергія, яку потрібно витратити, щоб із молекули (атома) вибити електрон, називається енергією іонізації. Процес, зворотний іонізації, називається рекомбінацією: позитивні і негативні іони, або позитивні іони і електрони, зустрічаючись, возз'єднуються між собою, утворюючи нейтральні атоми і молекули.

Проходження електричного струму через гази називається газовим розрядом. Струм у газі при невеликих напругах, існуючий тільки під впливом зовнішнього іонізатора, називається несамостійним газовим розрядом Якщо дію іонізатора припинити, то припиниться і струм, оскільки інших джерел іонів немає. Тому розряд і називається несамостійним.

При подальшому підвищенні напруги, сила струму різко зросте. Якщо тепер прибрати зовнішній іонізатор, розряд продовжуватиметься, оскільки необхідні для підтримки провідності газу іони тепер створюються самим розрядом. Газовий розряд, що зберігається після припинення дії зовнішнього іонізатора, називають самостійним газовим розрядом. Напруга, при якому він виникає, називають напругою запалення газового розряду або напругою пробою. Самостійний розряд підтримується за рахунок ударної іонізації електронами, прискореними електричним полем.

Залежно від умов протікання, розрізняють декілька типів самостійного газового розряду: 1) Тліючий розряд – виникає при низькому тиску газу; 2) Іскровий розряд – виникає при великих напруженостях електричного поля у газах при атмосферному тиску; 3) Дуговий розряд – виникає при атмосферному тиску газу, підтримується за рахунок високої температури катоду через інтенсивну термоелектронну емісію і термічну іонізацію молекул; 4) Коронний розряд – виникає при високому тиску газу у різко неоднорідному полі поблизу електродів із великою кривиною поверхні (наприклад, вістря).

Сильно іонізований газ, у якому концентрації позитивних і негативних іонів практично однакові, називається плазмою. До властивостей плазми відносяться: 1) високий ступінь іонізації газу (на границі – повна іонізація); 2) рівність нулю результуючого просторового заряду; 3) велика електропровідність; 4) свічення; 5) сильна взаємодія із електричними і магнітними полями; 6) коливання електронів плазмі із великою частотою (100 МГц); 7) одночасна «колективна» взаємодія величезної кількості частинок. Ці властивості визначають якісну своєрідність плазми, що дозволяє вважати її особливим, четвертим станом речовини.

Плазма – найпоширеніший стан речовини у Всесвіті. Із плазми складаються не тільки зірки. Наша Земля оточена плазмовою оболонкою – іоносферою, за межами якої існують радіаційні пояси, у яких також є плазма. Фізика плазми важлива і для розуміння багатьох процесів, що протікають у Космосі. Дослідження її властивостей, законів її руху і методів одержання складає зміст нового розділу сучасної фізики – фізики плазми.

ТЕСТОВІ ЗАВДАННЯ З РОЗДІЛУ “ЗАКОНИ ПОСТІЙНОГО СТРУМУ”