
poz053
.pdf
10
Произведем вычисления количества переданной теплоты на каждом этапе:
Q1 = 2100 Дж/кг град 1 кг (0 –(–20)град ) = 42000 Дж = 42 кДж;
Q2 = 3.3 105 Дж/кг 1 кг = 330000 Дж = 330 кДж;
Q3 = 4200 Дж/кг град 1 кг (100°C – 0°C ) = 420000 Дж = 420 кДж;
Q4 = 2.26 106 Дж/кг 1 кг = 2260000 Дж = 2260 кДж;
Q5 = 2200 Дж/кг град 1 кг (120°C – 0°C) = 44000 Дж = 44 кДж.
Вычислим полное количество переданной теплоты:
Q = (42 +330 + 420 + 2260 + 44) кДж = 3096 кДж .
Промежутки времени, соответствующие каждому этапу, можно определить по формулам:
τ1 |
= |
Q1 |
; τ2 |
= |
Q2 |
; τ3 |
= |
Q3 |
; τ4 |
= |
Q4 |
; τ5 |
= |
Q5 |
, |
|
|
|
|
|
|||||||||||
|
|
q1 |
|
q1 |
|
q1 |
|
q1 |
|
q1 |
|||||
где τ1 – время нагревания льда; τ2 – время таяния льда; τ3 – время нагревания воды; τ4 – время испарения воды; τ5 – время нагревания пара.
tоС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t, мин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
60 |
120 |
180 |
240 |
300 |
360 |
420 |
480 |
520 |
|||||||||||
–40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Произведем расчеты и по полученным данным построим график зависимости температуры от времени:
τ1 = 42000 Дж / 100 Дж/с = 420 с = 7мин; τ2 = 3,3·105 Дж / 100 Дж/с = 3300 с = 55 мин; τ3 = 420000 Дж / 100 Дж/с = 4200 с = 70 мин; τ4 = 2,26·106Дж / 100 Дж/с = 22600с = 377 мин; τ5 = 44000 Дж / 100 Дж/с = 440 с = 7,3 мин.
Ответ: Q = 3096 кДж.
Пример 3. Определить массу m2 воды, которая может быть превращена в лед при t2 = 0°C испарением эфира, масса которого m1 = 0,1 кг, а температура t1 = 20°С. Удельная теплота испарения эфира L = 3,8·105 Дж/кг, удельная теплота плавления льда λ = 3,3·105 Дж/кг, удельная теплоемкость эфира
11
СЭ = 2100 Дж/кг град, удельная теплоемкость воды СВ = 4200 Дж/кг град. Теплообмен происходит только между эфиром и водой. (Примечание: при решении задачи используются обозначения Q11, Q21, Q22 , которые не означают возведения в степень соответствующего значения Q2 или Q1, а соответствуют Q при опреде-
ленном процессе). |
|
|
|
|
|
|
|
|
|
|
|
Дано: |
|
|
|
|
Решение: |
|
|
||||
|
|
|
|
||||||||
m = 0,1 кг |
|
Рассмотрим последовательность процессов, проис- |
|||||||||
t1 = 20°C |
|
ходящих в системе вода-эфир: |
|
|
|||||||
СЭ = 2100 Дж/кг град |
|
вода: m, t |
замерзание |
лед: m |
, t |
|
|
|
|||
|
2 |
|
|
2 |
2 |
|
|
|
|||
СВ = 4200 Дж/кг град |
|
|
|
Q11 (теплота выделяется) |
|||||||
|
|
|
|||||||||
λ = 3,3·105 Дж/кг |
|
|
|
охлаждение |
|
|
|
|
|||
|
эфир: m1, t1 |
|
|
эфир: m1, t2 |
|
испарение |
|||||
L =3,8·106 Дж/кг |
|
|
|
Q21 (выделяется) |
|
Q22 (поглощается) |
|||||
|
|
|
|
||||||||
t2 = 0°C |
|
испарение |
|
|
|
|
|
|
|
|
|
|
эфир: m1, t2 |
|
|
|
|
|
|||||
m2 = ? |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Первоначально (очень быстро) эфир охлаждается и сразу же начинает испаряться. Для того, чтобы эфир полностью испарился, он должен получить количество теплоты: Qпол = Q22, причем Q22 > 0 и определяется по формуле:
Q22 = L m1.
Количество отданной теплоты складывается из теплоты, выделенной при охлаждении эфира Q21 от температуры t1 до температуры t2, и теплоты, выделенной при замерзании воды Q11 (Q21 < 0, Q11 < 0):
Qотд = |Q21| + |Q11| ,
Q21 = СЭ m1 (t2 – t1) , Q11 = λ m2 .
Составим уравнение теплового баланса либо в виде Q11 + Q21 + Q22 = 0, либо в виде Qпол = Qотд . Тогда в первом случае после преобразований, а во втором случае сразу можно записать:
L m1 = СЭ m1 (t1 – t2) + λ m2 .
Отсюда
λ m2 = L m1 – СЭ m1 (t1 – t2) , m2 = [ L – СЭ (t1 – t2) ] m1 / λ.
Произведем вычисления:
|
|
|
105 |
Дж |
|
Дж |
|
|
|
||
|
|
3.8 |
− 2100 |
20 град |
0,1 кг |
||||||
|
|
||||||||||
|
|
|
|
кг |
|
кг град |
|
|
|
||
m2 = |
|
|
|
|
|
|
= 0,102 кг =102 г. |
||||
|
|
|
|
3,3 105 |
Дж |
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
кг |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Ответ: m2 = 102 г.
12
Пример 4. С какой высоты должны падать дождевые капли, температура которых 20°С, чтобы при ударе о землю они испарялись. Теплоемкость воды СВ = 4200 Дж/кг град, удельная теплота парообразования L = 2,26 106 Дж/кг. Сопротивление воздуха не учитывать.
Дано: |
Решение: |
|
L = 2,26·106 Дж/кг |
Рассмотрим последовательность процессов, которые |
|
|
|
происходят с каплей дождя. Первоначально как тело, |
СВ = 4200 Дж/кг град |
|
|
t1 |
= 20°C |
поднятое на высоту Н, капля обладает потенциальной |
t2 |
= 100°C |
энергией, которую можно определить по формуле: |
g = 9,8 м/с2 |
ЕМЕХ 1 = m g H, (в верхней точке v0 = 0). |
|
Н = ? |
|
|
|
|
|
При падении тела его потенциальная энергия уменьшается, а кинетическая возрастает. После удара о землю капля останавливается и ее механическая энергия преобразуется во внутреннюю.
Воспользуемся законом сохранения и превращения энергии. Количество выделенной теплоты, которая пошла на нагревание капли до температуры кипения и на ее испарение, будем считать равным начальному значению механической энергии системы.
Qотд = ЕМЕХ 1;
Qпол = Q1 + Q2 ;
ЕМЕХ 1 = Q1 + Q2 ,
где Q1 = СВ m (t2 – t1) – количество теплоты, полученное при нагревании капли, Q2 = L m – количество теплоты, полученное при испарении капли.
m g H = СВ ·m ·(t2 – t1) + L·m , H = [ СВ (t2 – t1) + L ] / g.
Произведем расчеты:
|
|
Дж |
(100°С− 20°С)+ 2,26 |
106 |
Дж |
|
|
|
|
|
||
|
4200 |
|
|
|
|
|
||||||
|
кг град |
кг |
|
|
|
|
||||||
H = |
|
|
|
|
|
|
= 265 |
10 |
5 |
м = 265км. |
||
|
|
9,8 |
м |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
с2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: Н = 265 км.
Пример 5. На электрической плитке мощностью 800 Вт вода закипает за 10 мин. Чему равен к.п.д. плитки, если объем воды 1 л, ее удельная теплоемкость С = 4200 Дж/кг град, плотность воды составляет ρ = 1000 кг/м3, начальная температура воды t1= 20°C?

|
|
13 |
||
Дано: |
СИ |
Решение: |
||
Р = 800 Вт |
600 с |
По определению коэффициент полезного дей- |
||
τ = 10 мин |
ствия (к.п.д.) численно равен отношению полез- |
|||
V = 1 л |
10-3м3 |
ной работы к затраченной: |
||
С = 4200 Дж/кг·град |
|
|
AПОЛЕЗ |
|
|
|
η = к.п.д. = |
|
. |
ρ = 1000 кг/м3 |
|
АЗАТР |
||
t1 = 20°C |
|
В представленном случае полезная работа |
||
t2 = 100°C |
|
электрического тока расходуется на нагревание |
||
|
|
воды, поэтому можно принять: |
||
η = ? |
|
|||
|
|
АПОЛЕЗ = Q, где Q = C m (t2 – t1). |
||
Совершенная электрическим током работа равна: АЗАТР = Р · τ . Предварительно определим массу нагреваемой воды через плотность и
объем
m = ρ V = 1000 кг/м3 10-3 м3 = 1 кг.
Тогда для определения к.п.д. имеем формулу:
|
|
η = |
Q |
|
= C m (t2 −t1) . |
|
||
|
|
P τ |
|
|
||||
|
|
|
|
P τ |
|
|||
Произведем вычисления: |
|
|
|
|
|
|||
4200 |
Дж |
|
1 кг (100°С − 20°С) |
|
||||
кг град |
= 0,7 . |
|||||||
η = |
|
|
|
|||||
|
|
800 Вт 600 с |
||||||
|
|
|
|
|||||
Ответ: η = 0,7.
Пример 6. При обработке стальной детали на токарном станке была совершена работа, равная 750 кДж. 60% этой работы пошло на нагревание детали массой 5 кг. На сколько градусов нагрелась деталь? Удельная теплоемкость ста-
ли С = 500 Дж/кг град. |
|
|
|
|
Дано: |
|
Решение: |
||
|
||||
А=750 к Дж=75·104Дж |
|
Изменение внутренней энергии тела происходит за |
||
η = 60% = 0,6 |
|
счет части совершенной работы: |
||
С= 500 Дж/кг·град |
|
η A = Q , |
||
m = 5 кг |
|
где η = 0,6; Q = C·m· ∆t – количество теплоты, полу- |
||
|
|
ченное деталью при ее нагревании. |
||
∆t = ? |
|
|||
|
|
Тогда η A = C · m · ∆ t или ∆ t = |
η A |
. |
|
|
|||
|
|
|
C m |
|
14
Произведем вычисления: ∆t = |
0,6 75 104 |
Дж |
=180°С. |
|||
500 |
Дж |
|
5 кг |
|||
|
|
|||||
|
кг град |
|
||||
|
|
|
|
|||
Ответ: ∆ t = 180°С.
Задачи для самостоятельного решения
1.На сколько градусов повысилась температура 200 г воды, если ей была передана вся теплота, выделившаяся при полном сгорании 2 г спирта? Удельная теплоёмкость воды составляет 4200 Дж/(кг °С). Теплота сгорания спирта равна 2,7 107 Дж/кг.
2.Температура воды массой 5 кг повысилась от 7 до 53°С при опускании в неё нагретой железной гири. Определите массу этой гири, если после опускания её в воду температура гири понизилась от 1103 до 53°С. Удельная теплоёмкость воды 4200 Дж/(кг °С), железа 460 Дж/(кг °С).
3.Какое количество теплоты необходимо затратить на превращение в пар 200 г ртути, взятой при температуре 57°C? Удельная теплоемкость ртути 138 Дж/(кг·°C), удельная теплота парообразования 2,89·105 Дж/кг, температура кипения ртути 357°C.
4.Две тонны меди нагревают от 153°C до температуры плавления (1083°C). Сколько потребуется каменного угля, если вся выделяющаяся при сгорании топлива теплота пойдет на нагревание меди? Удельная теплоемкость меди 380 Дж/(кг·°C). Теплота сгорания каменного угля 3,1·107 Дж/кг.
5.На испарение 300 г эфира, взятого при температуре кипения (35°С), было затрачено 0,12 106 Дж теплоты. Определите удельную теплоту парообразования эфира.
6.Стальное сверло массой 42 г при остывании от 140 до 40°С выделяет столько же теплоты, сколько необходимо для нагревания воды массой 92 г от 35 до 40°С. Определите удельную теплоёмкость стали. Удельная теплоёмкость воды 4200 Дж/(кг °С).
7.На газовой плите нагрели 2 кг воды в алюминиевом чайнике массой 1 кг от 20 до 80°С. Сколько природного газа потребовалось для этого, если считать, что вся теплота, выделившаяся при сгорании, пошла на нагревание воды и чайника? Удельная теплоемкость воды 4200 Дж/(кг °С), алюминия 880 Дж/(кг °С), теплота сгорания природного газа 4,4 107 Дж/кг.
15
8.На нагревание воды массой 600 г, взятой при температуре 0°С, израсходовано 214,2 кДж теплоты. До какой температуры при этих условиях нагрелась вода? Удельная теплоемкость воды 4200 Дж/(кг °С).
9.Какое количество теплоты выделится при конденсации 0,5 кг водяного пара, взятого при температуре 100°С, остывании образовавшейся при этом воды и ее превращении в лед? Удельная теплота парообразования воды 2,3 106 Дж/кг, удельная теплоемкость 200 Дж/(кг °С), удельная теплота плавления льда 3,4 105 Дж/кг.
10.На нагревание воздуха в комнате объемом 50 м3 затрачено 645 кДж теплоты. Определите, на сколько градусов повысилась температура воздуха в комнате за счет этой теплоты. Плотность воздуха 1,29 кг/м3, а удельная теплоемкость 1000 Дж/(кг °С).
11.В ведро налито 5 л воды, температура которой 9°С. Сколько кипятку необходимо долить в ведро, чтобы температура стала 30°С?
12.Сколько теплоты выделилось при замерзании бассейна площадью 8000 м2, если толщина образовавшегося льда при 0°С составляет 50см, а перво-
начальная температура воды 4°С? Удельная теплоемкость воды 4200 Дж/(кг °С), температура кристаллизации 0°С, удельная теплота плавления льда 3,4 105 Дж/кг, плотность льда 900 кг/м3.
13.В спиртовку налито 80 г спирта. 25% теплоты, выделяющейся при его сгорании, используется полезно. Хватит ли этого количества спирта, чтобы испарить 450 г воды, взятой при температуре кипения (100°С)? Теплота сгорания спирта 2,7 107 Дж/кг, удельная теплота парообразования воды
2,3 106 Дж/кг.
14.При трении двух железных брусков друг о друга была совершена работа, равная 4200 Дж. Определите величину изменения внутренней энергии этих брусков, если 40% всей энергии, затраченной при совершении работы, пошло на их нагревание.
15.Определите КПД примуса, если для нагревания 2 кг воды от 10 до 100°С в нем сожгли 40 г керосина. Удельная теплоемкость воды 4200 Дж/(кг °С), теплота сгорания керосина 4,6 107 Дж/кг.
16.Молот массой 3 т падает с высоты 2 м на медную болванку массой 100кг. Определите, на сколько увеличилась температура болванки, если вся механическая энергия молота пошла на изменение ее внутренней энергии. Удельная теплоемкость меди 380 Дж/(кг·°C).
16
17.В вагранке нагрели 10 т чугуна от 0 до 1160°С. Определите, сколько кокса при этом сожгли, если известно, что КПД вагранки 20%.Удельная теплоёмкость чугуна 460 Дж/(кг°С).Теплота сгорания кокса 2,9 107 Дж/кг.
18.На нагревание воды от 10 до 80°С затрачено 0,6 кг дров, теплота сгорания которых 1,0 107 Дж/кг. Определите массу нагреваемой воды, если КПД нагревателя 30%. Удельная теплоемкость воды 4200 Дж/(кг°С).
17
Раздел 2. Электрические явления
Электрический ток представляет собой направленное перемещение электрических зарядов (электронов или ионов). Наименьшим (элементарным) зарядом обладает электрон, его заряд равен 1,6 ·10-19 Кл.
Сила тока в проводнике определяется по формуле:
I = qt ,
где q – заряд, прошедший через поперечное сечение проводника; t – время.
Закон Ома для участка цепи:
I = UR ,
где U – напряжение на участке, R – сопротивление участка.
Сопротивление проводника определяется его материалом (удельным сопротивлением ρ) и параметрами (длиной L и площадью поперечного сечения S):
R = ρ SL .
Удельное сопротивление ρ численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м2.
Последовательное соединение проводников
1. |
Сила тока в любых частях цепи одна и та же, |
|
|
|
|
|
|
|
|
|
U |
|||||||||||
|
т.е. I = I1 = I2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
R2 |
||||||||
2. |
Общее сопротивление участка цепи при по- |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
I |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
следовательном соединении равно сумме со- |
|
|
|
|
|
U1 |
|
U2 |
|||||||||||||
|
противлений отдельных проводников: Rоб = R1 + R2. |
|
|
|
|
|
||||||||||||||||
3. |
Полное напряжение участка цепи равно сумме напряжений на отдельных |
|||||||||||||||||||||
|
участках: U = U1 + U2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Параллельное соединение проводников |
|
|
|
|
|
|
I1 |
R1 |
|||||||||||||
1. |
Напряжение на участке цепи АВ и на концах |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
всех параллельно соединенных проводников од- |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
I А |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
В |
|||||||||||||||||
|
но и то же: U = U1 = U2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
R2 |
|||||||||||
2. |
Сила тока в неразветвленной части цепи равна |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
сумме сил токов в отдельных |
параллельно |
соединенных |
проводниках: |
||||||||||||||||||
|
I = I1 + I2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
Сопротивление участка цепи с параллельно соединенными сопротивлениями |
|||||||||||||||||||||
|
определяется по формуле: |
1 |
= |
1 |
+ |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18
Для двух сопротивлений R = |
R1 R2 |
(общее сопротивление двух провод- |
|
|
|||
|
R + R |
2 |
|
|
1 |
|
|
ников, соединенных параллельно, всегда меньше сопротивления любого из проводников).
Работа постоянного тока на участке цепи с напряжением U определяется по формулам:
A = I U t = I |
2 |
R t = |
U 2 |
t , |
|
R |
|||
|
|
|
|
где t – время прохождения тока, R – сопротивление проводника, I – сила тока. Работа тока за время, равное одной секунде, называется мощностью:
P = |
A |
= I U = I |
2 |
R = |
U 2 |
. |
t |
|
R |
||||
|
|
|
|
|
Закон Джоуля-Ленца: количество теплоты, выделившееся в проводнике за время t, прямо пропорционально квадрату силы тока I, проходящего по проводнику, сопротивлению проводника R и времени прохождения тока t:
Q = I 2 R t .
Вокруг проводника с электрическим током существует магнитное поле, которое можно обнаружить с помощью магнитной стрелки. Направление поля определяется по правилу правого винта. N – северный полюс магнитной стрелки; S – южный полюс магнитной стрелки.
Поле прямого проводника с током Поле постоянного магнита Ток направлен к нам
N S
N S N S 

 S N
S N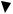
 I S
I S
N
I
|
N |
|
S |
N |
|
S |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Северный |
|
|
Южныйполюс |
||||
полюсмагнита |
|
|
магнита |
||||
Поле проводника с током |
Направление силы, |
в виде катушки |
действующей на проводник с током, |
|
помещенный в магнитное поле |
N S
S I N
S
N
I
N  S
S
N S
 F
F
19
Примеры решения задач
Пример 1. Сопротивление алюминиевого провода длиной 2 м и площадью поперечного сечения 1 мм2 равно 0,56 Ом. Определить удельное сопротивление
алюминия. |
|
|
|
|
|
|
|
|
|
|
Дано: |
|
СИ |
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|||
L = 20 м |
|
|
|
|
Воспользуемся формулой для определения сопротив- |
|||||
S = 1 мм2 |
|
10-6 м2 |
|
ления: R = ρ |
L |
. |
|
|
|
|
R = 0,56 Ом |
|
|
|
|
|
|
||||
|
|
|
|
|
S |
|
R S |
|
||
|
|
|
|
|
|
|
|
|
|
|
ρ = ? |
|
|
|
|
Выразим удельное сопротивление ρ = |
. |
||||
|
|
|
|
|
L |
|||||
|
|
|
|
|
|
|
||||
Произведем вычисления: |
|
|
|
|||||||
|
|
|
ρ = |
0.56 Ом 10−6 м2 |
= 28 10−9 Ом м. |
|
|
|||
|
|
|
|
|
20 м |
|
|
|
||
Ответ: 28 10−9 Ом м.
Пример 2. Через лампу накаливания проходит ток 0,8 А. Сколько свободных электронов проходит через поперечное сечение нити лампы накаливания за
10 с? Заряд электрона 1,6 10-19 Кл. |
|
|
|
||||
Дано: |
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|||
I = 0,8 A |
Сила тока определяется через заряд, прошедший по про- |
||||||
t = 10 c |
|
q |
|
I t |
|
||
|
воднику: I = |
|
, где q = N e , т.е. I t = N e , откуда N = |
|
. |
||
e = 1,6 10-19 Кл |
t |
e |
|||||
|
|
0,8 А 10 с |
|
|
|
||
N = ? |
Произведем расчеты: N = |
= 0,5 1020 . |
|
|
|||
|
|
|
|||||
|
|
|
1,6 10-19 Кл |
|
|
|
|
|
|
|
|
|
Ответ: N = 0,5 1020 . |
||
|
|
|
|
|
|||
Пример 3. Сопротивление нити накаливания 50 Ом, сопротивление подводящих проводов 0,4 Ом. Определить падение напряжения на лампе накалива-
ния и напряжение на подводящих проводах. |
|
|
|
||||
Дано: |
|
Решение: |
|
|
|
||
|
|
|
|
||||
R1 |
= 50 Ом |
При |
последовательном соеди- |
|
R1 |
R2 |
|
R2 |
= 0,4 Ом |
нении |
токи в сопротивлениях |
|
|||
|
|
|
|||||
|
|
|
|||||
I = 4 А |
одинаковы I = I1= I2. |
|
|
|
|
||
|
I |
|
|||||
|
|||||||
U1 = ? |
|
|
|
|
|
|
|
U2 = ? |
|
|
|
|
|
|
|
