
- •Функция. Предел функции в точке.
- •Условия монотонности функции на промежутке. Выпуклость функции на промежутке. Точки перегиба функции.
- •Первообразная и неопределенный интеграл функции. Методы интегрирования функций.
- •Определенный интеграл. Интегрируемость непрерывной функции.
- •Суммы Дарбу. Пусть Составим суммы . Они называются нижней и верхней суммами Дарбу.
- •Определенный интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.
- •Приложения определенного интеграла.
Математический анализ
Функция. Предел функции в точке.
Понятие функции. Числовые функции числового аргумента. График функции. Способы задания функции. Элементарные глобальные свойства функций (ограниченность, неограниченность, монотонность, периодичность, четность, нечетность). Предел функции в точке по Коши и по Гейне. Эквивалентность двух определений. Единственность предела функции.
Непрерывность функции.
Различные определения непрерывности функции в точке. Локальные свойства непрерывной в точке функции (ограниченность, сохранение функцией знака). Непрерывность суммы, произведения и частного двух непрерывных функций. Понятие сложной функции. Непрерывность сложной функции. Теоремы Больцано-Коши о промежуточных значениях непрерывных на сегменте функций и их применения. Первая теорема Вейерштрасса об ограниченности непрерывной на сегменте функции. Вторая теорема Вейерштрасса о достижении непрерывной на сегменте функцией своих граней.
Производная и дифференцируемость функции. Правила дифференцирования.
Понятие производной функции в точке. Геометрический и механический смысл производной функции в точке. Уравнение касательной и нормали к графику функции в точке. Дифференцируемость функции в точке. Правила дифференцирования суммы, произведения и частного двух дифференцируемых функций. Дифференцирование сложной и обратной функции. Производные основных элементарных функций (тригонометрических, логарифмической, показательной и степенной функций).
Условия монотонности функции на промежутке. Выпуклость функции на промежутке. Точки перегиба функции.
Теорема Лагранжа и её геометрическое истолкование. Необходимое и достаточное условие постоянства функции на промежутке. Необходимое и достаточное условие монотонности функции на промежутке. Экстремумы функции. Условия существования точек экстремума функции. Определение выпуклости (вогнутости) функции на промежутке. Достаточное условие выпуклости дважды дифференцируемой функции. Точки перегиба. Необходимое условие существования точки перегиба функции. Достаточное условие существование точки перегиба функции.
Первообразная и неопределенный интеграл функции. Методы интегрирования функций.
Задачи, приводящие к восстановлению функции по её производной (задача о вычислении пройденной пути по мгновенной скорости, задача о вычислении мгновенной скорости по ускорению, задача о вычислении переменной массы по известной плотности). Понятие первообразной функции. Свойства первообразных функций.
Понятие неопределенного интеграла и его свойства. Таблица интегралов основных элементарных функций. Метод непосредственного интегрирования. Интегрирование методом подстановки и по частям.
Определенный интеграл. Интегрируемость непрерывной функции.
Задачи, приводящие к понятию определенного интеграла (задача о площади
криволинейной трапеции, задача о вычислении работы под действием переменной силы). Понятие определенного интеграла. Суммы Дарбу и их свойства (обзорно). Необходимое и достаточное условие интегрируемости. Интегрируемость непрерывной функции. Основные свойства определенного интеграла.
Определенный интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.
Определение функции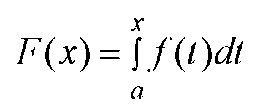 -
определенного интеграла с перемен
-
определенного интеграла с перемен
ным верхним пределом. Свойства функции F(х): непрерывность и дифференцируе- мость. Существование первообразной для непрерывной функции. Формула Ньютона-Лейбница и её значение для интегрального исчисления. Связь между определенным и неопределенным интегралами функции.
Приложения определенного интеграла.
Площадь криволинейной трапеции. Площадь криволинейного сектора в полярной системе координат. Объем тела вращения. Вычисление длины кривой. Вычисление площади поверхности вращения. Работа силы. Вычисление статических моментов и координат центра тяжести кривой.
Ответы
Функция. Предел функции в точке.
Понятие функции. Числовые функции числового аргумента. График функции. Способы задания функции. Элементарные глобальные свойства функций (ограниченность, неограниченность, монотонность, периодичность, четность, нечетность). Предел функции в точке по Коши и по Гейне. Эквивалентность двух определений. Единственность предела функции.
Пусть даны два множества произвольной
природы: .ОтношениеfмеждуAиB, при котором каждому
элементу из множества А соответствует
не более одного элемента изB,
называетсяфункцией или отображением.
.ОтношениеfмеждуAиB, при котором каждому
элементу из множества А соответствует
не более одного элемента изB,
называетсяфункцией или отображением.
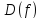 -
область определения,
-
область определения, - область значения. Функцию называютобратимой, если двум различным
значениям аргумента соответствуют
различные значения функции
- область значения. Функцию называютобратимой, если двум различным
значениям аргумента соответствуют
различные значения функции .
Еслиfотношение обратимое,
то обратное к нему отношение
.
Еслиfотношение обратимое,
то обратное к нему отношение ,
также будет функцией. Эту функцию
называютобратнойк функцииf.
,
также будет функцией. Эту функцию
называютобратнойк функцииf.
Если
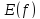 –
числовое множество, то функциюfназываютчисловойфункцией. Если
–
числовое множество, то функциюfназываютчисловойфункцией. Если –
числовое множество, тоfназываютчисловой функцией числового
аргумента.
–
числовое множество, тоfназываютчисловой функцией числового
аргумента.
В декартовой системе координат
упорядоченная пара
 однозначно определяет точку
однозначно определяет точку .
Множество точек плоскости
.
Множество точек плоскости сопоставлено функцииf,
такие что
сопоставлено функцииf,
такие что называетсяграфикомфункцииfи
обозначается
называетсяграфикомфункцииfи
обозначается .
Геометрическое определение функции:
любая прямая, параллельная оси 0Yимеет не более одной общей точки с
графиком.
.
Геометрическое определение функции:
любая прямая, параллельная оси 0Yимеет не более одной общей точки с
графиком.
Способы задания функции: табличный, аналитический с помощью формул, параметрический, графический, словесный, рекуррентный (явно или неявно задаются несколько первоначальных членов и дается формула для нахождения остальных членов).
Функцию fназовемограниченной сверху на М, если .
Наименьший из верхних границ для функцииfназываетсяверхней
граньюэтой функции
.
Наименьший из верхних границ для функцииfназываетсяверхней
граньюэтой функции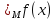 .
Функцияfназываетсянеограниченной сверхуна М, если
.
Функцияfназываетсянеограниченной сверхуна М, если .
Функциюfназовемограниченной снизу на М, если
.
Функциюfназовемограниченной снизу на М, если .
Наибольшее из нижних границ для функцииfназываетсянижней
гранью этой функции
.
Наибольшее из нижних границ для функцииfназываетсянижней
гранью этой функции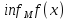 .
Функцияfназываетсянеограниченной снизуна М, если
.
Функцияfназываетсянеограниченной снизуна М, если .
Функцияfназываетсяограниченной, если она ограничена
сверху и снизу. Функцияfназываетсянеограниченной, если
она не ограничена сверху и снизу.
.
Функцияfназываетсяограниченной, если она ограничена
сверху и снизу. Функцияfназываетсянеограниченной, если
она не ограничена сверху и снизу.
Функцию fназовеммонотонно
возрастающейна М если ,
т.е. большему значению аргумента
соответствует большее значение функции,строго возрастающей
,
т.е. большему значению аргумента
соответствует большее значение функции,строго возрастающей .
Функциюfназываюткусочно-монотонной на М, если М можно
разбить на конечное число подмножеств,
в каждом из которыхfмонотонна.
.
Функциюfназываюткусочно-монотонной на М, если М можно
разбить на конечное число подмножеств,
в каждом из которыхfмонотонна.
Множество М называется симметричнымотносительноx=0, если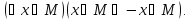 Функцияfназываетсячетнойна М, если М-симметричное
множество и
Функцияfназываетсячетнойна М, если М-симметричное
множество и Функцияfназываетсянечетнойна М, если М-симметричное
множество и
Функцияfназываетсянечетнойна М, если М-симметричное
множество и
Множество М подмножества
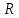 называетсяпериодическимс периодом
Т>0, если оно наряду с каждым числомxсодержит в себе числаx+Tиx-T,т.е.
называетсяпериодическимс периодом
Т>0, если оно наряду с каждым числомxсодержит в себе числаx+Tиx-T,т.е. Периодическое множество неограниченно.
Период Т – наименьшее положительное
число. Функцияпериодическаяс
периодом Т если:D(f)
периодическое множество и
Периодическое множество неограниченно.
Период Т – наименьшее положительное
число. Функцияпериодическаяс
периодом Т если:D(f)
периодическое множество и
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Определение
предела по Гейне.
Число A
называется пределом
функции f (x)
в точке a,
если эта функция определена в некоторой
окрестности точки a
за исключением, быть может, самой точки
a,
и для любой последовательности
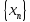 такой, что
такой, что сходящейся к числуa,
соответствующая последовательность
значений функции
сходящейся к числуa,
соответствующая последовательность
значений функции
 сходится к числуA.
сходится к числуA.
Определения предела функции по Коши и по Гейне эквивалентны.
Если функция в точке а имеет предел, то он единственный.
Непрерывность функции.
Различные определения непрерывности функции в точке. Локальные свойства непрерывной в точке функции (ограниченность, сохранение функцией знака). Непрерывность суммы, произведения и частного двух непрерывных функций. Понятие сложной функции. Непрерывность сложной функции. Теоремы Больцано-Коши о промежуточных значениях непрерывных на сегменте функций и их применения. Первая теорема Вейерштрасса об ограниченности непрерывной на сегменте функции. Вторая теорема Вейерштрасса о достижении непрерывной на сегменте функцией своих граней.
Пусть на множестве Dопределена .
Функциюf(x)
называютнепрерывнойв точке
.
Функциюf(x)
называютнепрерывнойв точке по Коши, если
по Коши, если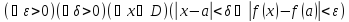 .
Функциюf(x)
называютнепрерывнойв точке
.
Функциюf(x)
называютнепрерывнойв точке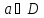 по Гейне, если
по Гейне, если т.е.
для любой
т.е.
для любой элементов множестваD,
сходящейся к т.aпоследовательность
элементов множестваD,
сходящейся к т.aпоследовательность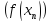 соответсвующих значений функции имеет
своим пределомf(a).
Из
соответсвующих значений функции имеет
своим пределомf(a).
Из эквивалентность определений. Функцию
назовемнепрерывнойв т.аслева
(справа), если существует левый (правый)
предел
эквивалентность определений. Функцию
назовемнепрерывнойв т.аслева
(справа), если существует левый (правый)
предел и он равен
и он равен
Локальное св-во ограниченности.
Если функция f(x) непрерывна в т.a,
то найдется такая окрестность этой
точки, в которой функция f(x) будет
ограничена. Если функцияfнепрерывна т.аи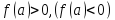 ,
то в достаточно малой окрестности т.афункцияfположительна
(отрицательна).
,
то в достаточно малой окрестности т.афункцияfположительна
(отрицательна).
Локальное св-во сохранение функцией
знакаЕсли функции f(x) и g(x) непрерывны
в точке а, то их сумма и произведение
так же будут непрерывны в этой точке.
Если дополнительно: ,
то частное функций f(x) и g(x) есть функция
непрерывная.
,
то частное функций f(x) и g(x) есть функция
непрерывная.
Сложная функция, функция от функции. Если величина yявляется функцией отu, то естьу=f(u), и, в свою очередь, функцией отх, то естьu=j(х), тоуявляется сложной функцией отх, то естьy=f[(x)],определённой для тех значенийх, для которых значенияj(х)входят в множество определения функцииf(u). В таком случае говорят, чтоуявляется сложной функцией независимого аргументах, аu- промежуточным аргументом.
Если функция u(x)непрерывна в точкеа, а функцияf(u)непрерывна в соответствующей точкеu0=f(x0),то сложная функцияf(u(x))непрерывна в точкеа.
Th1 Больцано-Коши.
Пустьf(x)определена и непрерывна
на замкнутом отрезке [a, b] и на концах
этого отрезка принимает разные по знаку
значения. Тогда такая, чтоf(c) = 0.
такая, чтоf(c) = 0.
Th2 Больцано-Коши.
Пусть f(x) определена и непрерывна на
отрезке [a;b]
и Тогда
Тогда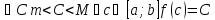 .
.
Th1 Вейерштрасса.
Пустьf(x)определена и непрерывна на замкнутом
отрезке [a,b].
Тогда существуют конечныеmиMтакие, что .Другими
словами, функция, непрерывная на замкнутом
отрезке, ограничена на этом отрезке и
сверху и снизу.
.Другими
словами, функция, непрерывная на замкнутом
отрезке, ограничена на этом отрезке и
сверху и снизу.
Th2 Вейерштрасса.Пустьf(x)определена и непрерывна на замкнутом
отрезке [a,b].
Тогда ,
такие, что
,
такие, что .Другими
словами, непрерывная функция, определенная
на замкнутом отрезке, достигает в нем
своих супремума и инфимума.
.Другими
словами, непрерывная функция, определенная
на замкнутом отрезке, достигает в нем
своих супремума и инфимума.
Производная и дифференцируемость функции. Правила дифференцирования.
Понятие производной функции в точке. Геометрический и механический смысл производной функции в точке. Уравнение касательной и нормали к графику функции в точке.Дифференцируемость функции в точке. Правила дифференцирования суммы, произведения и частного двух дифференцируемых функций. Дифференцирование сложной и обратной функции.Производные основных элементарных функций (тригонометрических, логарифмической, показательной и степенной функций).
Если приращение
 можно записать в виде
можно записать в виде гдеA-независимое от
гдеA-независимое от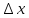 дейст. число,
дейст. число, -бесконечно
малая функция аргумента
-бесконечно
малая функция аргумента при
при ,
то функциюfназываютдифференцируемойв т.
,
то функциюfназываютдифференцируемойв т. .
Главная часть приращения
.
Главная часть приращения называетсядифференциаломфункцииfв т.
называетсядифференциаломфункцииfв т. и обозначается
и обозначается .
.
Всякая
дифференцируемая в точке функция
является и непрерывной в ней. Функция
fдиф-ема в т. ТиТТ,К существует конечный предел
ТиТТ,К существует конечный предел .
Предел отношения приращения функции к
приращению аргумента при
.
Предел отношения приращения функции к
приращению аргумента при называетсяпроизводнойфункцииfв т.
называетсяпроизводнойфункцииfв т. и обозначается
и обозначается .Тогда
дифференциал
.Тогда
дифференциал ,
приращение
,
приращение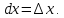
Геометрический смысл производной.
Рассмотрим график функцииy =f(x ). Из рис.1 видно, что для
любых двух точек A и B графика функции: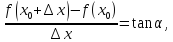 где
где![]() -
угол наклона секущей AB. Таким образом,
разностное отношение равно угловому
коэффициенту секущей. Если зафиксировать
точку A и двигать по направлению к ней
точку B, то
-
угол наклона секущей AB. Таким образом,
разностное отношение равно угловому
коэффициенту секущей. Если зафиксировать
точку A и двигать по направлению к ней
точку B, то![]() неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда следует:
производная функции в точке есть угловой
коэффициент касательной к графику этой
функции в этой точке. Другими
словами, производная
функции в точке x0
равняется тангенсу угла наклона
касательной к графику функции в этой
точке. В этом и состоитгеометрический смысл производной.
Геометрическидифференциалфункции
df – это приращение ординаты касательной
к графику функции в данной точке при
изменении абсциссы точки на dx.Выведем
уравнение касательнойк графику
функции в точке A (x0,f(x0
) ). В общем случае уравнение прямой с
угловым коэффициентом f’(x0
) имеет вид:y=f’(x0
) · x + b . Чтобы найтиb,
воспользуемся тем, что касательная
проходит через точку A:f(x0
) =f’(x0 ) ·x0
+ b , отсюда,b=f(x0
) –f’(x0 ) · x0
, и подставляя это выражение вместоb, мы получимуравнение
касательной:y= f(x0
) +f’(x0 ) · (x –
x0 ) .Нормалью
к графику функции y = f (x)
в точке A (x0; y0)
называется прямая, проходящая через
точку A
и перпендикулярная касательной к этой
точке. Она задается уравнением
неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда следует:
производная функции в точке есть угловой
коэффициент касательной к графику этой
функции в этой точке. Другими
словами, производная
функции в точке x0
равняется тангенсу угла наклона
касательной к графику функции в этой
точке. В этом и состоитгеометрический смысл производной.
Геометрическидифференциалфункции
df – это приращение ординаты касательной
к графику функции в данной точке при
изменении абсциссы точки на dx.Выведем
уравнение касательнойк графику
функции в точке A (x0,f(x0
) ). В общем случае уравнение прямой с
угловым коэффициентом f’(x0
) имеет вид:y=f’(x0
) · x + b . Чтобы найтиb,
воспользуемся тем, что касательная
проходит через точку A:f(x0
) =f’(x0 ) ·x0
+ b , отсюда,b=f(x0
) –f’(x0 ) · x0
, и подставляя это выражение вместоb, мы получимуравнение
касательной:y= f(x0
) +f’(x0 ) · (x –
x0 ) .Нормалью
к графику функции y = f (x)
в точке A (x0; y0)
называется прямая, проходящая через
точку A
и перпендикулярная касательной к этой
точке. Она задается уравнением
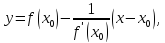 что следует из свойства угловых
коэффициентов перпендикулярных друг
другу прямых. В случае бесконечной
производной
что следует из свойства угловых
коэффициентов перпендикулярных друг
другу прямых. В случае бесконечной
производной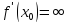 касательная
в точкеx0
становится вертикальной и задается
уравнением x = x0,
а нормаль – горизонтальной: y = y0.
Механический смысл производной.
Рассмотрим простейший случай:
движение материальной точки вдоль
координатной оси, причём закон движения
задан: координатаxдвижущейся точки – известная функцияx(t) времениt. В течение
интервала времени отt0доt0+
касательная
в точкеx0
становится вертикальной и задается
уравнением x = x0,
а нормаль – горизонтальной: y = y0.
Механический смысл производной.
Рассмотрим простейший случай:
движение материальной точки вдоль
координатной оси, причём закон движения
задан: координатаxдвижущейся точки – известная функцияx(t) времениt. В течение
интервала времени отt0доt0+![]() точка перемещается на расстояние:
x(t0+
точка перемещается на расстояние:
x(t0+![]() )
- x(t0) =
)
- x(t0) =![]() ,
а еёсредняя скорость равна:
va =
,
а еёсредняя скорость равна:
va =
![]() /
/![]() .
При
.
При![]()
![]() 0
значение средней скорости стремится к
определённой величине, которая называетсямгновенной скоростью v(t0)
материальной точки в момент времениt0. Но по определению производной
мы имеем:
0
значение средней скорости стремится к
определённой величине, которая называетсямгновенной скоростью v(t0)
материальной точки в момент времениt0. Но по определению производной
мы имеем: отсюда,
v(t0)=x’(t0), т.e.
скорость – это производная координаты
по времени. В этом и состоитмеханический смыслпроизводной.
Аналогично,ускорение – это
производная скорости по времени:a=v’ (t). Дифференциал
показывает путь пройденной точкой за
время
отсюда,
v(t0)=x’(t0), т.e.
скорость – это производная координаты
по времени. В этом и состоитмеханический смыслпроизводной.
Аналогично,ускорение – это
производная скорости по времени:a=v’ (t). Дифференциал
показывает путь пройденной точкой за
время при равномерном движении со скоростью
при равномерном движении со скоростью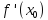 .
.
Th
Правила
диф-ния. Если
функции f
и
g
дифференцируемы
в точке
 то в этой же точке дифференцируемы
сумма, произведение и частное (если
то в этой же точке дифференцируемы
сумма, произведение и частное (если )
этих
функций, причем
)
этих
функций, причем
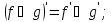

 .
.
Th
Производная
обратной функции.
Пусть функция y=f(x)
непрерывна и строго монотонна в некоторой
окрестности т. и при
и при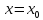 существует производная
существует производная ,
тогда обратная функция
,
тогда обратная функция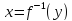 имеет производную в точке
имеет производную в точке причем
причем ,
т.о. производная обратной функции равна
обратной величине производной данной
функции.
,
т.о. производная обратной функции равна
обратной величине производной данной
функции.
Th
Производная
сложной функции.
Пусть на множестве D
существует сложная функция
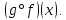 Пусть функцияy=f(x)
диф-ема в т.
Пусть функцияy=f(x)
диф-ема в т. и функцияz=g(y)
диф-ема в соответствующей точке
и функцияz=g(y)
диф-ема в соответствующей точке
 ,
тогда сложная функция
,
тогда сложная функция в т.
в т. также диф-ема причем
также диф-ема причем Производная сложной функции по независимой
переменной равна произведению этой
функции по промежуточному аргументу и
производной внешней функции по независимой
переменной.
Производная сложной функции по независимой
переменной равна произведению этой
функции по промежуточному аргументу и
производной внешней функции по независимой
переменной.
Производные элементарных функций.
а) Тригонометрические функции.

Мы
воспользовались первым замечательным
пределом
 и свойством предела произведения.
Итак,
и свойством предела произведения.
Итак,
 Аналогично
Аналогично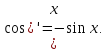 Производные
тангенса и котангенса можно найти как
производные частного:
Производные
тангенса и котангенса можно найти как
производные частного:

б)
Обратные тригонометрические функции.
Рассмотрим функцию y = arcsin x.
На отрезке
 обратной
к ней функцией будетx = sin y.
Продифференцируем эту функцию по x,
считая y
функцией от x:
обратной
к ней функцией будетx = sin y.
Продифференцируем эту функцию по x,
считая y
функцией от x:
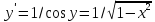 .
Аналогично выводятся формулы и для
других обратных функций. Получаем:
.
Аналогично выводятся формулы и для
других обратных функций. Получаем:

в)
Степенная и показательная функции.
Рассмотрим функцию
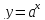 .
Для нее
.
Для нее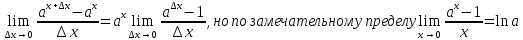 ,
еслиa > 0, a ≠ 1,
то
,
еслиa > 0, a ≠ 1,
то

При
x > 0,
 .
.
г)
Логарифмическая функция.
Рассмотрим функцию
 .
Еслиa > 0, a ≠ 1,
то
.
Еслиa > 0, a ≠ 1,
то
 .
.
д)Степенно-показательная
функция. Рассмотрим
функцию


 т.о. производная функции
т.о. производная функции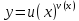 равна сумме двух слагаемых, из которых
первое совпадает с производной из того
предположения, что функция рассматривается
как показательная, а второе – в
предположении, что функция степенная.
равна сумме двух слагаемых, из которых
первое совпадает с производной из того
предположения, что функция рассматривается
как показательная, а второе – в
предположении, что функция степенная.
е)Параметрически
заданные функции. Если
 диф-емы в т.
диф-емы в т. и
и строго монотонна в неокторой окрестности
т.t
и
строго монотонна в неокторой окрестности
т.t
и
 соответсвующий точке
соответсвующий точке будет также диф-ема и производная
будет также диф-ема и производная
