10.2.2 Подготовка задачи к решению с помощью плм

Для подбора ПЛМ минимальной сложности, следует уменьшить по возможности число термов в рассматриваемой системе функций. Содержанием минимизации функций будет поиск кратчайших дизъюнктивных форм. Вести поиск минимальных по числу термов представлений задачи следует до уровня, когда число термов становится равным l — параметру обеспечиваемому ПЛМ. Дальнейшая минимизация не требуется. Если размерность имеющих­ся ПЛМ обеспечивает решение задачи в ее исходной форме, то минимиза­ция не требуется вообще, т. к. не ведет к сокращению оборудования.

10.2.3 Программирование плм

Программирование ПЛМ, выполняемое пользователем, проводится с помощью специальных устройств (программаторов) и сведения для них должны иметь определенную форму. Имеются программато­ры, которые принимают в качестве информации о ПЛМ таблицу функционирования (истинности), однако удобнее задавать сведения о самих перемычках. Символы, используемые при таком задании сведений для программирования ПЛМ:

• Н — переменная входит в терм в прямом виде, т. е. нужно оставить це­лой перемычку прямого входа и пережечь перемычку инверсного входа;

• L — переменная входит в терм в инверсном виде, т. е. нужно сохранить перемычку у инверсного входа и пережечь у прямого;

• «—» — переменная не входит в терм и не должна влиять на него, т. е, нужно пережечь перемычки обоих входов.

Оставление перемычек у обоих входов переменной как бы устраняет из матрицы соответствующую схему И, поскольку в силу равенства выход этой схемы всегда нулевой и не влияет на работу матрицы ИЛИ.

• А — указывается в выходном столбце (столбце функции) и свидетельствует о связи данной схемы И с выходом ПЛМ через матрицу ИЛИ. Пе­ремычка должна быть сохранена;

• « . » — указывает на то, что данная схема И не подключается к выходу и должна иметь пережженную перемычку в матрице ИЛИ.

В принятой символике для программирования ПЛМ взятого ранее примера сведения будут заданы таблицей (табл. 10.1).

Таблица 10.1

x1	x2	x3	x4	F1	F2	F3
L	L	H	—	A	A	.
—	H	L	—	A	.	.
H	—	—	L	A	.	A
H	L	L	—	.	A	.
H	H	—	H	.	A	.
—	H	L	H	.	A	.
H	L	—	—	.	.	A

10.2.4 Упрощенное изображение схем плм

Схемы ПЛМ достаточно громоздки, и поэтому изображать их желательно с максимально возможным упрощением. Используются изображения, в кото­рых многовходовые элементы И, ИЛИ условно заменяются одновходовыми.

Единственная линия входа таких элементов пересекается с несколькими ли­ниями входных переменных. Если пересечение отмечено точкой, данная переменная подается на вход изображаемого элемента, если точки нет, то переменная на элемент не подается. Пример многовходового конъюнктора с входами показан на рис. 10.4, а. Схема рис. 10.2, а в новом упрощенном изображении имеет вид, приведенный на рис. 10.4, б.

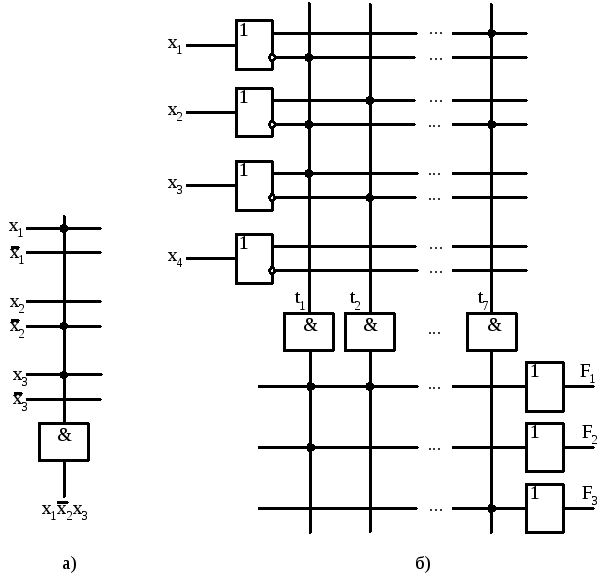
Рис. 10.4. Упрощенное изображение схемы многовходового логического элемента (а) и ПЛМ (б)