1.2 Прохождение импульсов через rc-цепи.

1.2.1 Напряжение и ток в rc-цепях под воздействием единичного скачка.

На вход RC-цепи (см. рис.1.6) поступает единичный скачок напряжения, изображённый на рис.1.7.

Рис. 1.6 -Принципиальная схема RC-цепи. Рис. 1.7 -График единичного скачка.

Определим реакцию цепи на единичный скачок, т.е. установим зависимости:

; ;;

Уравнение скачка, т.е. напряжение на входе цепи описывается в виде:

;

;

Начальные условия: ,,.

Уравнение второго закона Кирхгофа для цепи имеет вид:

.

С учётом ,, получим;

Запишем дифференциальное уравнение описывающее RC-цепь в стандартном виде:

,

с начальными условиями ,,. (1.1)

Решение такого дифференциального уравнения ищется в виде суммы свободной и вынужденной составляющих:

.

Свободная составляющая записывается в виде: , и описывает собственный переходной процесс в цепи при отсутствии возмущающего воздействия (т.е. при нулевой правой части уравнения), следовательно,

;

обозначив , запишем это уравнение в операторной форме:

.

Поскольку изменяется во времени переходного процесса по экспоненциальному закону, т.е., то

, отсюда находим корень характеристического уравнения

.

Подставив его значение в уравнение свободной составляющей, получим:

, где, постоянная времениRC-цепи,

тогда

.

При ,;

Вынужденная составляющая, обусловленная правой частью уравнения, имеет место после окончания переходных процессов (теоретически при , практически при) определяется в виде:

.

Теперь запишем полное решение дифференциального уравнения:

.

В этом выражении неизвестной величиной является амплитуда A.ОпределимАиз начальных условий:

;

.

Окончательное решение дифференциального уравнения имеет вид:

; (1.2)

Зависимость при разных постоянных времениRC-цепи приведены на рис.1.8

Рис. 1.8

Напряжение на выходе RC-цепи имеет вид:

.

Зависимости при различных значенияхприведены на рис.1.9.

Рис. 1.9

Поскольку , то(1.4)

Зависимость приведена на рис.1.10.

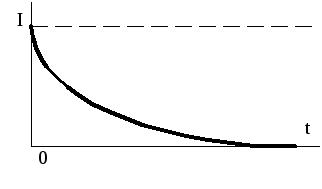
Рис. 1.10

1.2.2 Дифференцирующая (укорачивающая) и разделительная rc-цепи.

Дифференцирующей цепью называют такую цепь, сигнал на выходе которой имеет значения, пропорциональные в каждый момент производной от входного сигнала. Следовательно, . КоэффициентКдолжен выражаться в секундах, в противном случае размерность левой и правой частей равенства не будет одинакова. Идеальным дифференцирующим устройством можно считать конденсаторСили катушкуL. Например, при использовании конденсатораСможно считать входным сигналом напряжение на нём, а выходным – токв цепи. Эти переменные связаны известным соотношением, т.е. ток в цепи пропорционален производной от входного напряжения. Однако использовать эту схему для практических целей нельзя, так как она не содержит элемента, который обеспечивал бы какую-либо регистрацию значений тока, измерение его значений.

Для того чтобы получить выходной сигнал в форме, удобной для наблюдения или регистрации, в цепь последовательно включают токочувствительный прибор с внутренним сопротивлением R. В простейшем случаи это может быть резисторR. Напряжение на котором пропорционально току.

Рассмотренная RC-цепочка может выполнять функции как дифференцирующей (укорачивающей) при, так и разделительной цепи, если.

На рис.1.11 показаны графики напряжений итакой цепочки.

Рассмотрим два режима:

1. Дифференцирующая цепь – , при этом возможны два варианта: а); б);

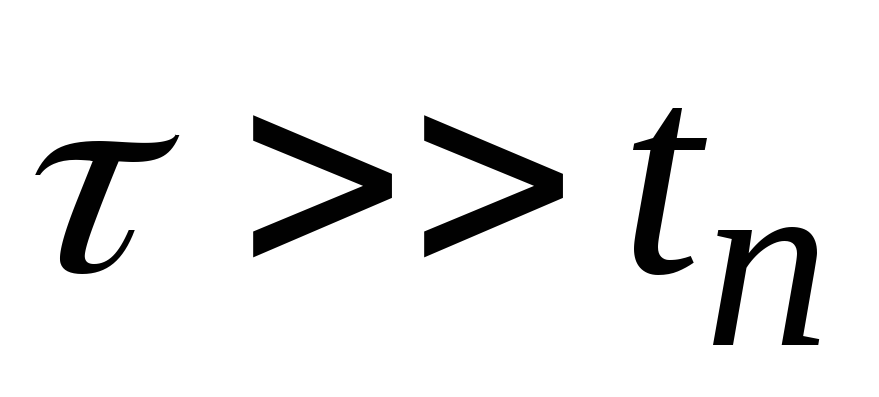2. Разделительная цепь – , при этом также: а); б);

а) б)

Рис. 1.11 - а) режим 1 – , б) режим 2 –.

1. Рассмотрим дифференцирующею цепочку под воздействием импульсной последовательности (рис.1.12).

Рис. 1.12 -Принципиальная схема укорачивающей RC-цепочки

При импульсе конденсатор Сзаряжается под воздействием зарядного тока, при паузе – разряжается, обуславливая разрядный ток. При этом.

Допустим ,тогда им можно пренебречь ().

Рассмотрим режим I, вариант а):,.

После окончания импульса (момент времени ).

В период паузы () разряд конденсатораСполучается полный, т.к.;

Рис. 1.13

;

.

Тогда

;

При получим:

.

Значит получена идеальная дифференцирующая цепь. Следовательно для того чтобы цепь была дифференцирующей необходимо выполнение трёх условий:

1. ;

2. ;

3. ;

При этом график напряжения при наличии импульсной последовательности на входе будет иметь следующий вид (рис.1.14):

Рис. 1.14 - График напряжения дифференцирующей цепи при наличии импульсной последовательности на входе.

Режим I, вариант б):,:

Графики напряжений иприведены на рис.1.15. В этом режиме с момента времениимеют место, в отличие от варианта а), новые начальные условия. Такой режим называют режимом негармонических возмущений.

В период импульса переходные процессы аналогичны рассмотренным в варианте а), а в период паузы конденсатор Сне успевает разрядиться до нуля за время, поэтому нулевые начальные условия не выполняются и для дифференцирующей цепочки такой вариант неприемлем.

Рис. 1.15

Режим IIпри,обеспечивает вариант разделительной цепочки.

Вмомент времени, после действия импульса, (см. рис.1.16), а в момент времениимеют место нулевые начальные условия. Сигнал на выходе повторяет сигнал на входе. Следовательно, такая цепочка является разделительной

Рис. 1.16

РежимII, при,, аналогичен варианту б) режимаI, поскольку в момент временитакже имеют место новые, ненулевые начальные условия (рис.1.17) (режим негармонических возмущений). Для разделительной цепи такой вариант неприемлем.

(б)

Рис. 1.17