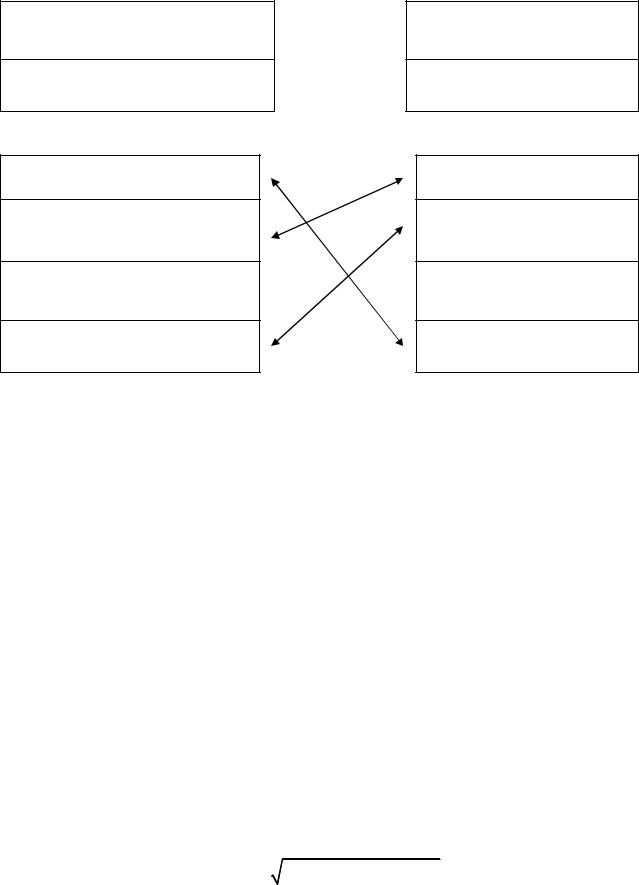
Сn - ЭТО
Сn хn – ЭТО
Ответ:
С0+ С1х+ С2 х2 + …+Сn хn. – ЭТО
+∞ n n∑=0cnx - ЭТО
Сn - ЭТО
Сn хn – ЭТО
n-ый КОЭФФИЦИЕНТ СТЕПЕННОГО РЯДА
ЧАСТИЧНАЯ СУММА СТЕПЕННОГО РЯДА
СТЕПЕННОЙ РЯД
n-ый ЧЛЕН СТЕПЕННОГОРЯДА
n-ый КОЭФФИЦИЕНТ СТЕПЕННОГО РЯДА
ЧАСТИЧНАЯ СУММА СТЕПЕННОГО РЯДА
Формы ответов других типов (выбор верного ответа из списка предложенных или ввод ответа с клавиатуры) уже хорошо знакомы по первому семестру.
При выполнении теста следует учесть, что последовательность тем заданий в тесте не совпадает с порядком следования разделов в программе, так как каждое конкретное тестовое задание формируется системой случайным образом.
Раздел 1. Функции двух переменных
Тема: «Функция многих переменных, область определения и область изменения»
Пусть D - некоторое множество точек плоскости Oxy. Если каждой точке M(x, y) из области D соответствует вполне определенное число z Е R, то говорят, что на множестве D задана функция двух переменных x и y. Переменные x и y называются независимыми переменными, или
аргументами, D - областью определения, или существования, функции, а
множество Е всех значений функции - областью ее значений. Функциональную зависимость z от x и y записывают в виде z=f(M), z = f(x, y), z = z(x, y), z = F(x, y) и т.д.
Расстояние между двумя точками A(x1, y1), B(x2, y2) на плоскости Oxy
вычисляют по формуле ρ(A,B)= (x − x )2 |
+ ( y |
2 |
− y )2 . |
||
2 |
1 |
|
|
1 |
|
Функция f(M) имеет пределом число |
A, |
lim f(M) = A , если разность f(M) - |
|||
|
|
|
M→M0 |
|
|
A есть бесконечно малая, когда ρ =ρ(Mo,M) → 0 при любом способе приближения на плоскости Oxy точки M к точке Mo
18
Функция f(x, y) называется непрерывной в точке Mo, если lim f(M) = f(M0 ) .
M→M0
ОБРАЗЕЦ 8.
Сопоставьте варианты из правой колонки вариантам из левой:
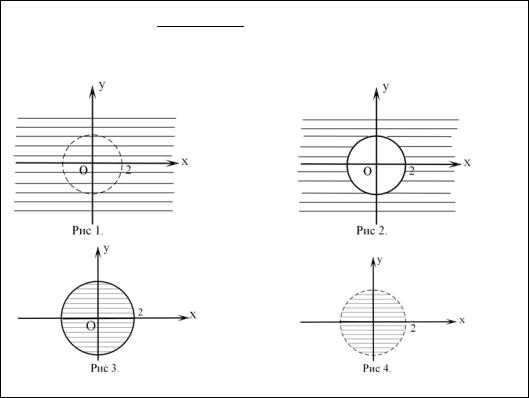
Если функция z = |
1 |
, то на плоскости хОу ее |
4 − y2 − x2 |
область определения имеет вид…
В ответе запишите номер рисунка.
Решение. Числитель дроби не должен равняться нулю. Приравняв его к нулю, получим: у 2 + х2 = 4. Это уравнение окружности с центром в начале координат и радиусом R=2. Поэтому область определения функции – вся плоскость кроме данной окружности, т.е. ответом является первый рисунок. Надо в строку ответов ввести число 1.
Тема «Частные производные 1-го и 2-го порядка»
Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение х переменной х. Тогда величина xz = f( x + x, y) – f(x, y) называется частным приращением функции по х.
Предел lim |
x z |
называется частной производной функции z = f(x, y) |
||||||
x→0 |
x |
|
|
|
|
|
|
|
по х. Обозначение: |
∂z |
; |
′ |
∂f (x, y) |
; |
′ |
||
∂x |
zx ; |
|
∂x |
fx (x, y). |
||||
|
|
|
|
|
|
|
||
Аналогично определяется частная производная функции по у. |
||||||||
|
|
|
∂z = lim |
f (x, y +Δy) − f (x, y) |
|
|||
|
|
|
|
|||||
|
|
|
∂y |
y→0 |
|
y |
||
Если функция f(x, y) определена в некоторой области D, то ее частные производные fx′(x, y) и fy′(x, y) тоже будут определены в той же области
или ее части.
19
Будем называть эти производные частными производными первого порядка. Производные этих функций будут частными производными
второго порядка.
∂2 z = f ′′(x, y);
∂x2 xx
∂∂x2∂zy = fxy′′(x, y);
∂2 z = f ′′(x, y);
∂y2 yy
∂∂y2∂zx = fyx′′(x, y);
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.
|
Пример. Вычислить частные производные |
∂z |
и |
∂z |
в произвольной |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
точке M (x, y) |
|
для |
функции |
f (x, y) = x2 −3xy + 2y2 |
и |
затем найти их |
||||||||||||||||||||
значения ∂z(M0 ) |
и |
∂z(M0 ) , если |
M0 (1,2) . |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. |
|
Имеем : |
∂z |
=(x2 −3xy + 2y2 )′x = |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (x2 )′x −(3xy)′x +(2y2 )′x = 2x −3y(x)′+0 = 2x −3y . |
|
|
|
|
|
|
|
|||||||||||||||||||
Тогда |
∂z |
|
|
= 2 1−3 2 = −4. Далее: |
∂z |
=(x2 |
−3xy +2y2 )′y = |
|
|
|||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
∂x |
|
M0 (1,2) |
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= (x2 )′y |
−(3xy)′y |
+(2y2 )′y |
= 0 −3x + 4y . Значит, |
|
|
|
|
|
|
|
|
|||||||||||||||
|
∂z |
|
|
= −3 1+2 4 =5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
M0 (1,2) |
|
|
|
|
∂z |
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Ответ: |
∂z |
|
= 2x −3y, |
= −3x +4y, |
|
|
= -4 , |
∂z |
|
|
= 5. |
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
∂x |
|
|
|
|
∂y |
|
|
∂x |
|
M0 |
|
∂y |
|
M0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Пример. Найти частные производные функции |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
∂z |
|
|
|
z=х2–3ху–4у2–х+2у+1. |
|
|
|
|
|
|
|
|
|||||||
|
Ответ: |
|
=2х–3у–1; |
∂z |
|
=2–3х–8у. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∂х |
|
∂у |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Задачи для самостоятельного решения |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
|
|
|
|
|
|
|
||||
|
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Найти сумму частных производных первого порядка функции |
|
|||||||||||||||||||||||
|
Z = x2 + y2 |
в точке (–2; 0,5) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2. |
Найти |
произведение |
частных |
производных |
первого |
порядка |
|
||||||||||||||||||
|
функции Z = arctg(x + y) в точке (0; 0) |
|
|
|
|
|
|
|
|
|||||||||||||||||
20
Если |
|
z = x ln |
|
y |
|
, то z′y |
равно … |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3. |
|
|
|
|
x2 |
|
|
|
x |
|
|
|
x |
|
|
|
|
y |
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
5) ln |
|
+ |
||||||||||||||
1) ху; |
2) |
|
|
; |
3) |
|
|
; |
4) |
|
|
|
|
; |
|
|
|
|
|
|||||||||
y |
y2 |
|
y |
|
x |
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если |
|
z = y ln |
|
x |
|
, то z′xy′ |
равно … |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
+1; 2) |
2y |
|
; 3) − |
y |
; 4) − |
|
x |
; 5) ln |
x |
+ |
1 |
|
||||||||||||||
1) |
|
|
|
|
||||||||||||||||||||||||
x |
|
x |
|
x2 |
|
y2 |
|
|
y |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|||||||||||||
5. |
|
1 |
|
z = 4ln(x + 4y) |
|
|
||||
Найти z′′yx в точке M 2; |
2 |
, если |
|
|
||||||
|
|
|
|
|
|
|
|
|
||
|
Вычислить частную |
производную |
∂2 z |
|
функции |
двух |
||||
6. |
∂x ∂y |
|||||||||
|
|
|
|
|
|
|
||||
|
переменных z = x3 y + xy2 −2x +3y −1 в точке (1;1) |
|
|
|||||||
|
|
|
|
|
||||||
|
Тема «Полный дифференциал и его приложения» |
|
|
|
||||||
|
Для функции f(x, y) выражение z |
= f( x + x, |
y + y) |
– f(x, y) |
||||||
называется полным приращением. Если функция f(x, y) дифференцируема в некоторой точке (х, у), то справедливо равенство
z = |
∂f (x, y) |
x + |
∂f (x, y) |
|
y + α1 x + α2 y , |
|
|||
∂x |
∂y |
|
|||||||
|
|
|
|
|
|
|
|||
где α1 и α2 – бесконечно |
малые функции |
при |
х |
→ 0 и |
у → 0 |
||||
соответственно. |
|
|
|
|
|
|
|
|
|
Полным дифференциалом функции |
z = |
f(x, |
y) |
называется |
главная |
||||
линейная относительно х и у часть приращения функции z в точке (х, у). Если функция f(x, y) дифференцируема, то полный дифференциал есть
dz = fx′(x, y)dx + fy′(x, y)dy
Для функции произвольного числа переменных:
df (x, y, z,...,t) = ∂∂fx dx + ∂∂fy dy +... + ∂∂ft dt
Для приближенных вычислений используют формулу:
f (x + x, y + y) ≈ f (x, y) + |
∂f (x, y) |
x + |
∂f (x, y) |
y |
|
∂x |
|
∂y |
|
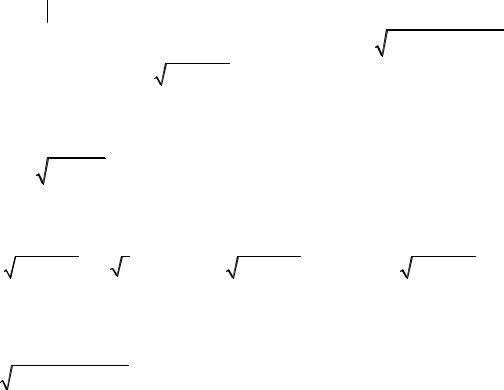
Пример. Найти полный дифференциал функции u = xy2 z . du = ∂∂ux dx + ∂∂uy dy + ∂∂uz dz
Решение. Находим частные производные:
21
∂u = y2 zxy2 z−1; |
∂u = xy2 z ln x 2yz; |
∂u |
= xy2 z ln x y2. |
||||||||
∂x |
|
|
|
∂y |
|
|
∂z |
|
|
|
|
Подставляем в формулу полного дифференциала: |
|
|
|
|
|||||||
du = y |
2 |
zx |
y2 z−1 |
dx + 2x |
y2 z |
yz ln xdy |
+ y |
2 |
x |
y2 z |
ln xdz |
|
|
|
|
|
|||||||
Пример. Найти в точке М(1;2) полный дифференциал функции |
|||||||||||
f (x, y) = x3 +3xy2 −5y +1). |
|
|
|
|
|
|
|
|
|||
Решение. Сначала находим частные производные: |
|
||||||||||
f ' (x, y) = (x3 +3xy2 −5y +1)' |
= |
|
|
|
|
||||||
=(x3 )'x +3y2 (x)'x +(−5y +1)'x =3x2 +3y2 .
Вданном случае числовые коэффициенты и переменная y выступали в роли констант: во втором слагаемом они были вынесены за скобки при дифференцировании, а третье слагаемое от x не зависело – поэтому его
производная по x равна нулю. Аналогично ищем производную по y (фиксируем x): x x
f 'y (x, y) = (x3 )'y +3x(y2 )'y −5( y)'y + (1)'y = 6xy −5
Здесь первое и четвертое слагаемые от y не зависят, их производные по y равны нулю.
Теперь вычисляем значения производных в данной точке: f 'x (1;2) =3 1+3 22 =15; f 'y (1;2) = 6 1 2 −5 = 7.
Воспользовавшись формулой полного дифференциала, окончательно имеем: df M =15dx + 7dy
Пример. Вычислить приближенно значение 1,041,99 + ln1,02 , исходя
из значения функции u = xy + ln z при x = 1, y = 2, z = 1.
Решение. Из заданного выражения определим частные приращения: x = 1,04 – 1 = 0,04, y = 1,99 – 2 = -0,01, z = 1,02 – 1 = 0,02.
Найдем значение функции u(x, y, z) в исходной точке M(1, 2, 1): u(1, 2, 1)= 12 + ln 1 =1
Находим частные производные функции u(x, y, z) в этой же точке M(1, 2, 1):
∂u |
|
y xy−1 |
2 1 |
|
∂u |
|
xy ln x |
|
∂u |
|
1 |
|
1 |
|
|
=1, |
|
= 0 , |
= |
z |
= |
||||||||
∂x |
= |
|
= |
|
∂y |
= |
|
∂z |
|
2 |
||||
2 xy +ln z |
2 1 |
2 xy +ln z |
2 xy +ln z |
|||||||||||
Полный дифференциал функции u равен:
du = 0,04 ∂∂ux −0,01 ∂∂uy +0,02 ∂∂uz =1 0,04 −0 0,01+ 12 0,02 = 0,04 + 0,01= 0,05
1,041,99 + ln1,02 = u(1,04; 0,99; 1,02) ≈u(1,2,1) + du =1+0,05 =1,05
Точное значение этого выражения: 1,049275225687319176.
22