Свойства математического ожидания

1. Математическое ожидание постоянной величины равно самой посто­янной

.

2. Постоянный множитель можно выносить за знак математического ожидания

.

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий

.

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий

.

5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю

Дисперсия случайной величины

Только математическое ожидание не может в достаточной степени характеризовать случайную величину.

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.

Дисперсией случайной величиныХназывается математическое ожидание квадрата ее отклонения от ее математического ожидания:

.

Дисперсия — это мера рассеяния случайной величины около ее математического ожидания.

Если Х— дискретная случайная величина, то дисперсию вычисляют по следующим формулам:

,

где а = М(Х);

.

Свойства дисперсии случайной величины

1. Дисперсия постоянной величины С равна нулю

.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат

.

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин

.

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий

.

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величиныХназывается арифметическое значение корня квадратного из ее дисперсии

.

Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность значений случайной величины.

Рассмотрим некоторые распределения дискретной случайной величины.

Биномиальный закон распределения

Если вероятность появления события Ав каждом испытании постоянна и равнар, то число появлений событияА— дискретная случайная величинаХ, принимающая значения 0, 1, 2, …,с вероятностями(формула Бернулли), где,,.

Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, вычисляется по формулам:

,

.

Распределение Пуассона

Если число испытаний велико, а вероятность появления события рв каждом испытании очень мала, то вместо формулы Бернулли пользуются приближенной формулой Пуассона

,

где число появлений события вn независимых испытаниях; m принимает значения .(среднее число появлений события вn испытаниях).

Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру , который определяет этот закон, т.е.

.

Геометрическое распределение

Дискретная случайная величинаимеет геометрическое распределение, если она принимает значения 1, 2, …,m, …(бесконечное, но счетное множество значений) с вероятностями

,

где .

Определение геометрического распределения корректно, так как сумма вероятностей

Случайная величина , имеющая геометрическое распределение, представляет собой числоmиспытаний, проведенных по схеме Бернулли, с вероятностьюрнаступления события в каждом испытании до первого положительного исхода.

Математическое ожидание и дисперсия случайной величины Х, имеющей геометрическое распределение с параметромрвычисляются по формулам:

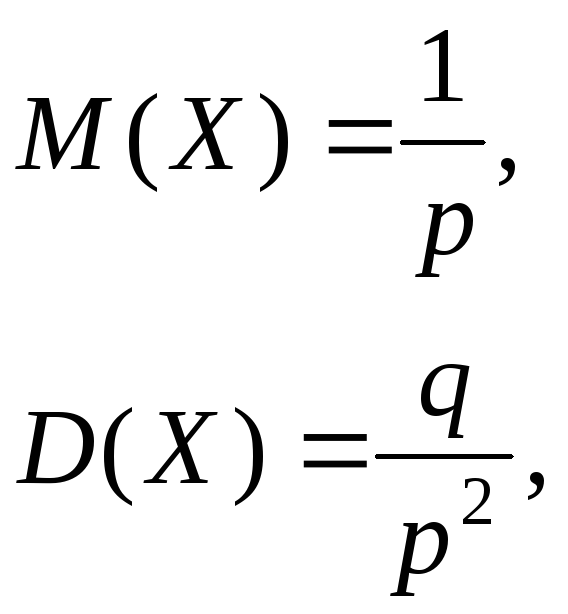
где