Нормальный закон распределения

Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и , если ее плотность вероятности имеет вид

.

Кривую нормального закона распределения называют нормальной или гауссовой кривой.

На рис. 8.14 приведены нормальная кривая р(х) с параметрами а и , т.е. , и график функции распределения случайной величины Х, имеющей нормальный закон

Рис. 8.14

Нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный , и две точки перегиба с ординатой .

Для случайной величины, распределенной по нормальному закону, , .

Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле

,

где .

Вероятность попадания значений нормальной случайной величины Х в интервал определяется формулой

.

Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину (по абсолютной величине), равна

.

«Правило трех сигм»: если случайная величина Х имеет нормальный закон распределения с параметрами а и т.е. , то практически достоверно, что ее значения заключены в интервале

.

Асимметрия нормального распределения А = 0; эксцесс нормального распределения Е = 0.

Пример 8.23. Определить закон распределения случайной величины Х, если ее плотность распределения вероятностей задана функцией

.

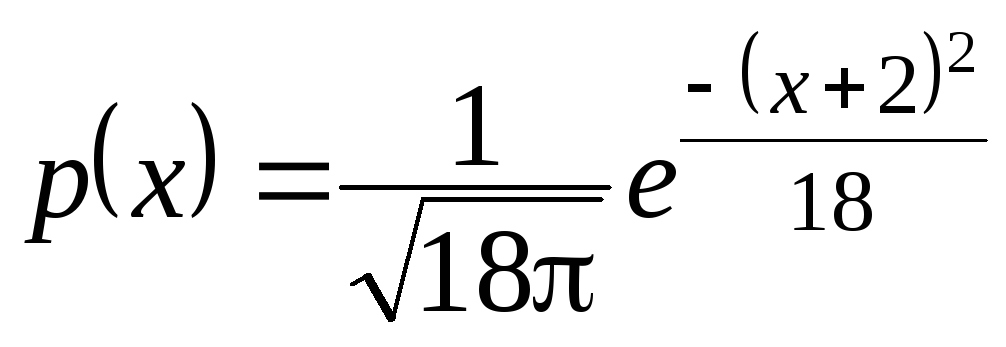Найти математическое ожидание, дисперсию и функцию распределения случайной величины Х.

Решение. Сравнивая данную функцию р(х) с функцией плотности вероятности для случайной величины, распределенной по нормальному закону, заключаем, что случайная величина Х распределена по нормальному закону с параметрами а = 1 и .

Тогда , , .

Функция распределения случайной величины Х имеет вид

.

Пример 8.24. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден. ед. и средним квадратическим отклонением 0,2 ден. ед.

Найти вероятность того, что цена акции: а) не выше 15,3 ден. ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед. С помощью «правила трех сигм» найти границы, в которых будет находиться текущая цена акции.

Решение. Так как а = 15 и , то

По «правилу трех сигм» и, следовательно, . Окончательно .

Пример 8.25. Автомат изготавливает детали, которые считаются годными, если отклонение Х от контрольного размера по модулю не превышает 0,8 мм. Каково наиболее вероятное число годных деталей из 150, если случайная величина Х распределена нормально с мм?

Решение. Найдем вероятность отклонения при и

Считая приближенно р = 0,95 и в соответствии с формулой

где  — наивероятнейшее число, находим при

откуда

Пример 8.26. Размер диаметра втулок, изготовленных заводом, можно считать нормально распределенной случайной величиной с математическим ожиданием а = 2,5 см и средним квадратическим отклонением см. В каких границах можно практически гарантировать размер диаметра втулки, если за вероятность практической достоверности принимается 0,9973?

Решение. По «правилу трех сигм» . Отсюда , т.е. .

Пример 8.27. Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Пусть математическое ожидание ее равно 175 см, а среднее квадратическое отклонение — 6 см. Определить вероятность того, что хотя бы один из наудачу выбранных пяти мужчин будет иметь рост от 170 до 180 см.

Решение. Найдем вероятность того, что рост мужчины будет принадлежать интервалу :

Тогда вероятность того, что рост мужчины не будет принадлежать интервалу (170; 180) q = 1 — 0,6 = 0,4.

Вероятность того, что хотя бы один из 5 мужчин будет иметь рост от 170 до 180 см равна

.

Пример 8.28. Браковка шариков для подшипников производится следу­ющим образом: если шарик не проходит через отверстие диаметром , но проходит через отверстие диаметром , то его размер считается приемлемым. Если какое-нибудь из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика есть случайная величина с характеристиками и . Определить вероятность того, что шарик будет забракован.

Решение.

Так как , то