Вища математика

xi = xi, i = 1,2,3…,n,

де — визначник матриці A, xi — визначник, утворений із заміною коефіцієнтів при xi вільними членами bi.

Метод Ґаусса

Нехай є система (3) n рівнянь з n невідомими

a11x1 + a12x2 +…+ a1nxn = b1a…21x1 + a22x2 +…+ a2nxn = b2

an1x1 + an2x2 +…+ annxn = bn

Визначимо елементарні операції:

•додавання до обох частин рівняння відповідних частин іншого рівняння, помножених на деякий множник.

•перестановка рівнянь в системі.

•перенумерування рівнянь або невідомих.

Застосовуючи ці операції, можна систему (3) привести до

трикутного виду:

21

А вже цю трикутну систему легко розв’язати, починаючи з останнього рівняння і поступово рухаючись знизу вверх.

Метод оберненої матриці

Нехай є система (4) n рівнянь з n невідомими

Ax = b,

Помножуючи обидві частини рівняння зліва на A–1, отримуємо

A–1Ax = A–1 b,

x = A–1 b.

Остання рівність є формулою розв’язку системи (4).

22

2. ВЕКТОРНА АЛГЕБРА ТА АНАЛІТИЧНА ГЕОМЕТРІЯ

Визначення

n-вимірним простором Rn називається множина упорядкованих сукупностей дійсних чисел (x1,x2,…,xn) в обраній системі координат. Точка простору позначається P(x1,x2,…,xn) Rn.

Наприклад, R1 — це пряма — одновимірний простір, R2 — це площина — двовимірний простір, R3 — це звичний для нас простір — тривимірний простір. Для n ≥ 4 наочність зникає.

Визначення

n-вимірним вектором a Rn називається напрямлений відрізок.

Це визначення вектора ґрунтується на наочності для n ≤ 3, тому розглянемо інший спосіб описання вектора. Визначимо n-вимірний вектор із Rn як довільний упорядкований набір дійсних чисел. Позначимо його a(a1,a2,…,an).

23

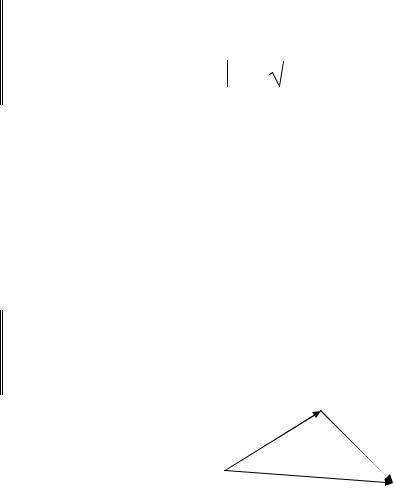
Визначення

Довжиною, або модулем вектора a(a1,a2,…,an) Rn називається число

2.1. ДІЇ НАД ВЕКТОРАМИ

Визначення

Сумою двох векторів a і b називається третій вектор c, напрямлений із початку вектора a у кінець b, якщо початок b збігається з кінцем a.

ab

c = a + b

Мал.1

Якщо a = (a1,a2,…,an) і b = (b1,b2,…,bn),

то c = a + b = (a1 + b1,a2 + b2,…,an + bn).

24

Визначення

Протилежним для вектора a вектором –a називається паралельний йому, рівний за довжиною і протилежно напрямлений вектор.

Якщо a = (a1,a2,…,an), то –a = (–a1,–a2,…,–an).

Щоб від вектора a відняти вектор b, треба до вектора a додати вектор –b, протилежний до вектора b.

Визначення

Добутком вектора a на число α називається вектор, довжина якого дорівнює α a , однаково напрямлений з a, якщо α > 0, і протилежно напрямлений з a, якщо α < 0.

Якщо a = (a1,a2,…,an), то αa = (α a1, α a2,…, α an).

Визначення

Вектори a і b, скалярний добуток яких дорівнює нулю, називаються

ортогональними.

Визначення

Векторним добутком векторів a і b називається вектор c такий, що

1)c = a b sin ϕ, де ϕ — кут між a і b (a,b) = a b,

2)c a і c b,

3)якщо c ≠ 0, то вектори утворюють праву трійку, тобто з кінця вектора c найкоротший поворот від a до b здійснюється проти годинникової стрілки.

Векторний добуток векторів позначається так: c = a b. Векторний добуток a a = 0 за визначенням. Нехай задано вектори a = (ax,ay,az), b = (bx,by,bz) у прямокутній системі координат i, j, k. Знайдемо їх векторний добуток a b.

c = a b = (ax i + ay j + az k)(bx i + by j + bz k) =

26

= axbx (i i) + axby (i j) + axbz (i k) +

+aybx (j i) + ayby (j j) + aybz (j k) +

+azbx (k i) + azby (k j) + azbz (k k).

Враховуючи, що i i = j j = k k = 0, а також, що i j=k, j i= –k, j k=i, k j= –i, k i=j, i k = –j, одержуємо

c = axby k – axbz j + aybz i – aybx k + azbx j – azby i =

Бачимо, що при i, j, k стоять визначники другого порядку. Отже, для знаходження векторного добутку отримали формулу

Визначення

Нехай задано три вектори a, b і c. Змішаним добутком трьох векторів називається число (a b) c.

27

2.2. ПРЯМА ЛІНІЯ НА ПЛОЩИНІ

Загальне рівняння прямої, що належить координатній площині x0y, має вигляд:

де C — вільний член.

Дослідимо загальне рівняння.

Якщо C = 0, то A x + B y = 0 — рівняння прямої, що проходить через початок координат.

Якщо A = 0, то B y + C = 0 — рівняння прямої, паралельної осі абсцис (перпендикулярної осі ординат).

Якщо B = 0, то A x + C = 0 — рівняння прямої, паралельної осі ординат (перпендикулярної осі абсцис).

Якщо A = C = 0, то y = 0 — рівняння осі абсцис. Якщо B = C = 0, то x = 0 — рівняння осі ординат.

Визначення

Розділимо обидві частини рівняння (6) на –C ≠ 0. Отримане рівняння

28

називається рівнянням прямої у відрізках на осях. Тут a і b —

відрізки, які відтинає пряма від координатних осей.

Визначення

Розділимо обидві частини рівняння (6) на B ≠ 0. Рівняння

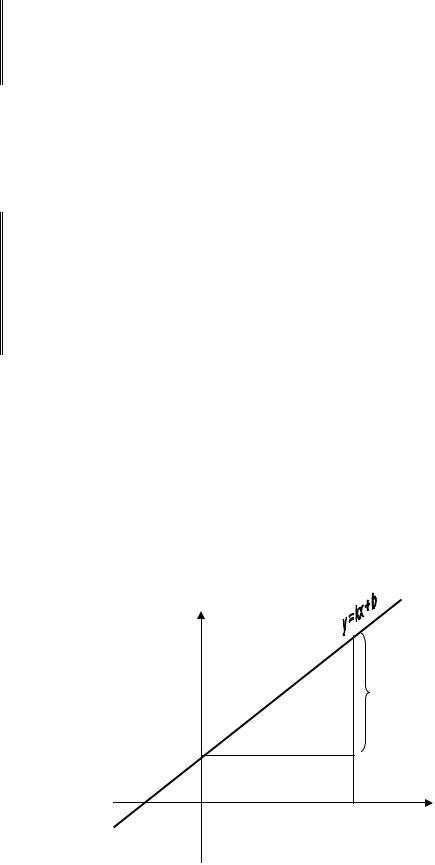
y = k x + b (8) називається рівнянням прямої з кутовим коефіцієнтом.

ординат даною прямою. Далі, із (8) k = = tg α, де α — це кут,

утворений прямою (8) з додатним напрямом осі абсцис:

y

y – b

α

αx

Мал. 2

29

Параметр k називають кутовим коефіцієнтом.

2.2.1. РІВНЯННЯ ПРЯМОЇ ЛІНІЇ, ЩО ПРОХОДИТЬ ЧЕРЕЗ 2 ТОЧКИ

Нехай дано 2 точки M1(x1,y1) і M2(x2,y2) на площині. Ці точки однозначно визначають пряму, яка проходить через них. Знайдемо рівняння цієї прямої.

Візьмемо довільну точку прямої M(x,y) і побудуємо вектори a, b:

a = M1M = (x – x1, y – y1),

b = M1M2 = (x2 – x1, y2 – y1).

Точка M(x,y) належить шуканій прямій тоді й тільки тоді, коли ці вектори лежать на цій прямій, тобто коли їх векторний добуток дорівнює нулю: a×b = 0, або

30