
Вища математика
.pdf
7. РЯДИ
7.1. ЧИСЛОВІ РЯДИ
7.1.1. ОСНОВНІ ПОНЯТТЯ. ЗБІЖНІСТЬ
Нехай задано числову послідовність {ak}, k N.
Визначення
|
|
∞ |
Числовим рядом називається нескінченна сума s = ∑ ak. Скінченна |
||
|
k=1 |
|
n |
|
∞ |
сума sn =∑ ak називається частинною сумою, сума rn = ∑ ak назива- |
||
k=1 |
|
k=n+1 |
ється залишком ряду, а ak — членом ряду. |
|
|
Визначення |
|
|
Якщо існує скінченна границя частинних сум lims |
n |
= s, то число s |
n→∞ |
|
|
називається сумою ряду, а сам ряд — збіжним. У протилежному випадку ряд називається розбіжним.
Теорема (необхідна умова збіжності ряду)

 Якщо ряд збіжний, то послідовність його членів прямує до нуля.
Якщо ряд збіжний, то послідовність його членів прямує до нуля.
111

Доведення
Якщо ряд збіжний, тобто за означенням збіжності існує скінчена границя частинних сум nlim→∞sn = s, то із рівності
an = sn – sn–1, n = 2,∞ ,
випливає, що nlim→∞an = nlim→∞sn – nlim→∞sn–1 = s –s = 0. Теорему доведено.
7.1.2. ВЛАСТИВОСТІ ЗБІЖНИХ РЯДІВ
∞ |
∞ |
∞ |
1. Якщо ряди ∑ ak і ∑ bk — збіжні, то ряди ∑ (ak ± bk) теж збіжні. |
||
k=1 |
k=1 |
k=1 |
∞ |
|
∞ |
2. Якщо ряд ∑ ak — збіжний, то ряд α∑ ak теж збіжний, де αR — |
||
k=1 |
|
k=1 |
будь-яка стала. |
|
|
∞ |
|
∞ |
3. Якщо ряд ∑ ak — збіжний, то ряд |
∑ ak — збіжний для будь-якого |
|
k=1 |
|
k=n+1 |
натурального значення n.
∞
4. (Критерій Коші) Ряд ∑ ak — збіжний тоді й лише тоді, коли ε>0
k=1
N(ε)>0 n>N і m N: sn+m – sn<ε.
7.1.3. ПРИКЛАДИ РЯДІВ
112

І. Гармонічний ряд: 1 + 12 + 13 +…+ 1n +… . Очевидно, необхідна умова збіжності ряду виконується. Але ряд розбігається. Доведемо це.
При будь-якому натуральному n маємо:
1 + |
1 |
+ ... + |
1 |
> |
1 |
+ |
1 |
+ ... + |
1 |
= |
1 |
, |
|
2n–1 |
|
2n |
|
2 |
|||||||
n n+1 |
|
|
2n |
|
2n |
|
||||||
тому, якщо вибирати ε(0;12), то для гармонічного ряду неможливо підібрати число N, яке вказано у критерії Коші. Це означає, що ряд розбігається.
ІІ. Ряд геометричної прогресії: 1 + q + q2 +…+ qn +… .
1) Якщо q ≥ 1, то необхідна умова збіжності ряду не виконується. Отже, у цьому випадку ряд розбігається.
2) Якщо 0 < q < 1, то необхідна умова збіжності ряду виконується, а сам ряд є сумою нескінченно спадаючої геометричної прогресії:
1+ q + q2 +…+ qn +… = 1 1– q.
7.1.4.ДОСТАТНІ ОЗНАКИ ЗБІЖНОСТІ РЯДІВ З ДОДАТНИМИ
ЧЛЕНАМИ
Нехай усі ak > 0, k = 1,∞ .
113

Інтегральна ознака Коші
Якщо функція f(x) невід’ємна і спадає на [0;+∞), то ряд
+∞
⌠
збіжний тоді й лише тоді, коли збігається інтеграл f(x)dx .
⌡
1
Ознака порівняння
∞
∑ f(k) —
k=1
Нехай 0 ≤ ak ≤ bk |
для будь-якого натурального k. Тоді якщо збігається |
|
∞ |
∞ |
∞ |
ряд ∑ bk, то збігається і ряд ∑ ak, а якщо розбігається ряд ∑ ak, то |
||
k=1 |
k=1 |
k=1 |
∞
розбігається і ряд ∑ bk.
k=1
Доведення
∞ |
∞ |
1. То, що збігається ряд ∑ bk, означає, що існує число b =∑ bk. Тоді |
|
k=1 |
k=1 |
n |
n |
з того, що 0 ≤ ak ≤ bk випливає, що sn = ∑ ak ≤ ∑ bk ≤ b. Ми |
|
k=1 |
k=1 |
отримали, що послідовність {sn} монотонно зростає і обмежена зверху, тобто має скінченну границю. За означенням випливає,
∞
що ряд ∑ ak збігається.
k=1
114

∞ |
∞ |
2. якщо розбігається ряд ∑ ak, то розбігається і ряд ∑ bk, тому що, |
|
k=1 |
k=1 |
|
∞ |
якщо б він збігався, то за доведеним збігався б і ряд ∑ ak, а це не |
|
так. |
k=1 |
|
|
Ознака Даламбера
∞ |
|
ak+1 |
∞ |
||
Якщо для ряду ∑ ak існує границя lim |
= l, то при l < 1 ряд ∑ ak |
||||
|
|||||
k=1 |
k→∞ |
a |
k |
k=1 |
|
|
|
||||
збігається, а при l > 1 ряд розбігається.
Ознака Коші
∞ |
|
|
∞ |
Якщо для ряду ∑ ak існує границя lim k |
ak |
= l, то при l < 1 ряд ∑ ak |
|
k=1 |
k→∞ |
|
k=1 |
|
|
||
збігається, а при l > 1 ряд розбігається.
7.1.5. ЗНАКОЗМІННІ РЯДИ
∞
Розглянемо знакочергуючий ряд ∑ (–1)kak, де ak > 0, k = 1,∞ .
k=1
115

Теорема Лейбниця
∞
Якщо послідовність {ak} спадає і прямує до нуля, то ряд ∑ (–1)k ak
k=1
збігається, до того ж |sk – s| ≤ ak+1.
Визначення
∞
Знакозмінний ряд ∑ ak (ak R) називається абсолютно збіжним,
k=1
∞
якщо ряд ∑ |ak| збігається.
k=1
Визначення
∞
Якщо знакозмінний ряд ∑ ak (ak R) збігається, але не абсолютно, то
k=1
він називається умовно збіжним.
Теорема Коші (критерій абсолютної збіжності)
∞
Ряд ∑ ak (ak R) абсолютно збіжний тоді й тільки тоді, якщо ε > 0
k=1
m
N, n > N i m N: ∑ |an+k| < ε.
k=1
116

Наслідок
∞
Якщо ряд ∑ ak (ak R) абсолютно збіжний, то він збігається.
k=1
Доведення
|
|
|
|
m |
m |
Це |
випливає |
з |
нерівності |
| ∑ an+k| ≤ ∑ |an+k|. Дійсно, згідно |
|
|
|
|
|
k=1 |
k=1 |
критерію |
Коші для |
абсолютно |
збіжних |
рядів, ε > 0 N, n > N i |
|
|
m |
|
|
|
|
m N: ∑ |an+k| < |
ε. Але тоді |
|
|
||
|
k=1 |
|
|
|
|
|
|
|
m |
m |
|
|
|
|
|∑ an+k| ≤ ∑ |an+k| < ε. |
||
|
|
|
k=1 |
k=1 |
|
Отже, з критерію Коші для рядів з довільними членами випливає, що ряд збігається.
7.2. СТЕПЕНЕВІ РЯДИ
7.2.1. ОСНОВНІ ПОНЯТТЯ ТА ТЕОРЕМИ
Визначення
Нехай на множині D задана послідовність функцій { fk(x)}, тоді ряд
∞
∑ fk(x) називається функціональним рядом.
k=1
117

Визначення
∞
Якщо ряд ∑ fk(x) збігається x D, то говорять, що ряд збігається на
k=1
множині D, а сама множина D називається областю збіжності функціонального ряду.
Визначення
Говорять, що послідовність функцій { fk(x)}рівномірно збігається до f(x) на множині D, якщо ε > 0 N, x D i k > N: | fk(x) – f(x)| < ε.
Визначення
∞
Говорять, що ряд ∑ fk(x) рівномірно збігається на множині D, якщо
k=1
на D рівномірно збігається послідовність його частинних сум.
Признак Вейєрштрасса
∞
Якщо числовий ряд з додатними членами ∑ ak збігається і x D i n:
k=1
∞
| fk(x)| ≤ ak, то функціональний ряд ∑ fk(x) збігається абсолютно і
k=1
рівномірно на множині D.
Визначення
∞
Степеневим рядом називається функціональний ряд ∑ ak(x – x0)k,
k=0
числа ak називаються коефіцієнтами ряду. 118
За допомогою заміни змінної z = x – x0 завжди можна привести
∞
степеневий ряд до вигляду ∑ akzk, тому ми обмежимось тим, що
k=0
∞
детальніше розглянемо ряд ∑ akxk.
k=0
Теорема Абеля
∞
Якщо степеневий ряд ∑ akxk збігається при деякім x = a ≠ 0, то він
k=0
збігається і x такого, що | x | < | a |. Якщо ж ряд розбігається при деякім x = a ≠ 0, то він розбігається і x такого, що | x | > | a |.
Теорема про область збіжності
Областю збіжності степеневого ряду є інтервал з центром у початку координат.
Доведення.
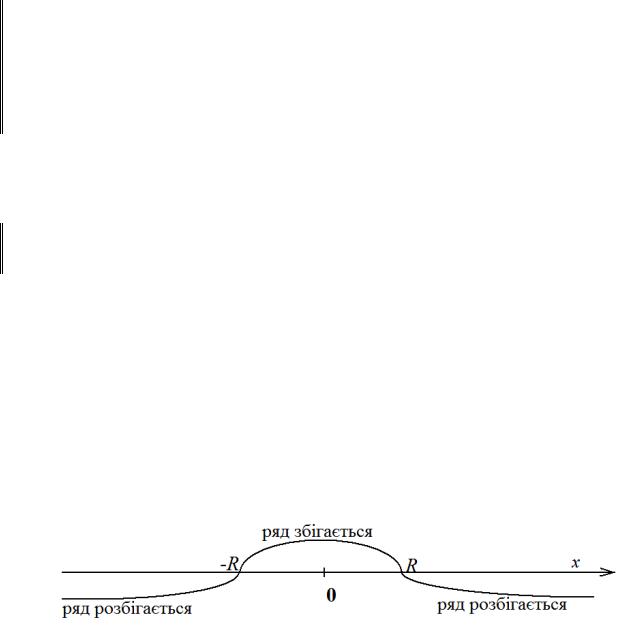
Дійсно, нехай x0 — точка збіжності степеневого ряду. Тоді інтервал (–|x0|;|x0|) заповнений точками абсолютної збіжності. Нехай x1 — точка розбіжності степеневого ряду. Тоді луч вправо від |x1| і луч вліво від –|x1| складаються із точок розбіжності.
Звідси можна вивести, що існує таке число R, що при |x| < R ми маємо точки абсолютної збіжності, а при |x| > R — точки розбіжності:
Теорему доведено.
119

Число R, яке з’явилося у доведенні теореми, називається радіусом збіжності степеневого ряду. Радіус збіжності степеневого ряду можна знайти за формулами
1 |
|
ak+1 |
|
1 |
|
k |
|
|
|
= lim |
, або |
= lim |
ak . |
||||||
R |
ak |
R |
|
||||||
k→∞ |
|
k→∞ |
|
|
|
||||
7.2.2. РЯД ТЕЙЛОРА
Якщо функція f(x) має похідні будь-якого порядку в околі точки x = a, то в цьому околі вона може бути розкладена у степеневий ряд, який називається її рядом Тейлора:
∞ |
f(k)(a) |
|
f(x) = ∑ |
k! |
(x – a)k. |
k=0 |
|
|
∞ |
f(k)(0) |
Якщо при цьому a = 0, то ряд ∑ |
k! xk називається рядом Маклоре- |
k=0 |
|
на. Наведемо розвинення деяких елементарних функцій у ряд Мак-
лорена:
∞ |
∞ |
k+1 |
∞ |
k |
|||
ex = ∑ |
1 |
xk, |
sin x = ∑ |
(–1) |
x2k–1, |
cos x = ∑ |
(2(–k1))! x2k, |
k! |
(2k–1)! |
||||||
k=0 |
k=0 |
|
|
k=0 |
|
||
∞ |
k+1 |
ln (1 + x) = ∑ |
(–1)k xk, |
k=1 |
|
∞ |
|
(1 + x)m = ∑ m (m–1) … (m–k+1) xk. |
|
k=0 |
k! |
|
|
120
