7. Екстремум функції двох змінних. Необхідні і достатні умови екстремуму.

Означення. Функція f(x, y) має в точці P1 (x1 , y1 ) локальний максимум, якщо існує окіл точки P1 , у якому для кожної точки P(x, y)  D( f) виконується нерівність f(P1 )  f(P), тобто приріст f(P1 ) зберігає знак у деякому околі точки P1 (рис. 1 ). Означення. Функція f(x, y) має в точці P2 (x2 , y2 ) локальний мінімум, якщо існує окіл точки P2 , у якому для кожної точки P(x, y)  D( f) виконується нерівність f(P2 )  f(P) , тобто приріст f(P2 ) зберігає знак у деякому околі точки P2 (рис. 2).

Теорема (необхідні умови екстремуму). Нехай P0 (x0 , y0 ) - точка локального екстремуму функції f(x, y) . Якщо існують частинні похідні fx' (P0 ) і fy' (P0 ) , то вони дорівнюють нулю. Доведення. Розглянемо випадок локального максимуму. Тоді у деякому околі точки P0 приріст f(P0 )  0 і, отже,

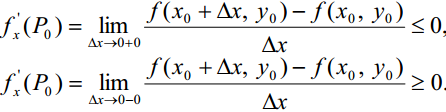
Звідси випливає, що fx' (P0 )  0. Аналогічно доводиться, що fy' (P0 )  0 . Теорему доведено. Означення . Точка P0 (x0 , y0 ) , у якій частинні похідні fx' і fy' дорівнюють нулю або не існують, називається критичною (або стаціонарною) точкою функції f(x,y) . Нехай P0 (x0 , y0 ) - стаціонарна точка функції f(x, y) . Позначимо

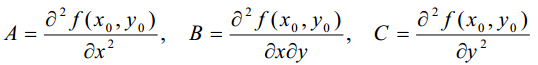, і покладемо

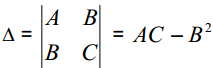
Тоді справедлива теорема (достатні умови екстремуму): якщо   0 , то функція має в точці P0 екстремум, а саме максимум при A  0 і мiнiмум при A  0 ; якщо   0 , то в точці P0 екстремуму немає; якщо   0 , то запитання про існування екстремуму залишається відкритим. 8. Умовний екстремум функції двох змінних. Метод множників Лагранжа.

Нехай потрібно знайти екстремум функції z= f(x, y) при умові, що на нелалежні змінні x і y

накладені додаткові обмеження: φ(x, y)=0 . Геометрично це означає, що точка P(x, y) лежить на

лінії, визначеній рівнянням φ(x, y)=0 . Якщо його можна розв’язати відносно y, тобто задати лінію явним рівнянням y=ψ(x) , то розв’язання зведеться до дослідження на екстремум функції однієї змінної z=f(x,ψ(x))=φ1 (x) .

З необхідної умови екстремуму функції однієї змінної маємо, що в термінах функції f дає(1)

Перетворимо умову (1) введенням функції (x, y) . Для цього продиференціюємо рівняння (x, y)  0 , вважаючи у ньому y як неявну функцію x:

(2)

Помножимо рівність (2) на число , яке підберемо потім, і додамо одержану рівність до рівності (1). Одержимо:

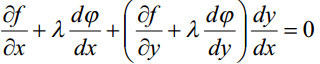(3)

Число  підберемо так, щоб Тоді з рівності (3) одержимо, що

Таким чином, критичні точки функції z  f(x, (x)) визначаються з системи рівнянь

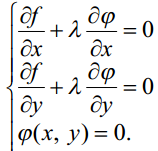(4)

Систему рівнянь (4) можна записати інакше, ввівши так звану функцію Лагранжа F(x, y)  f(x, y)  (x, y) . Тоді система набуває вигляду

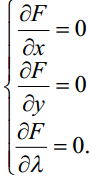(5)

Розв’язавши систему рівнянь (5), отримаємо критичні точки функції F(x, y) . Питання про існування екстремуму у критичних точках вирішується окремо, зокрема, з фізичних або геометричних міркувань. Для функції u  f(x, y, z) з двома рівняннями зв’язку 1 (x, y, z)  0 і 2 (x, y, z)  0 функція Лагранжа має вигляд F  f  1 1  2 2, а система (5) записується так:

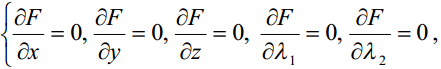(6) 9. Найбільше і найменше значення функції 2-х змінних у замкнутій області.

Функція z  f(x; y) , диференційовна в обмеженій області, набуває в ній найбільшого та найменшого значень в стаціонарних точках або в граничних точках. Таким чином, щоб знайти найбiльше і найменше значення функцiї в замкненій областi, треба: 1) знайти стацiонарнi точки, розмiщенi в данiй областi, i обчислити значення функцiї в цих точках; 2) дослідити функцію на екстремум на межі області; 3) з усix найдених значень вибрати найбiльше i найменше. 10.Диференціальні рівняння. Основні поняття і означення. Задача Коші.

Означення. Звичайним диференціальним рівнянням n - го порядку називається рівняння виду F(x, y, y', y'',..., y(n))  0, (1) де x - незалежна змінна, y  y(x) - невідома функція, y', y'', …, y(n) - похідні функції y(x) , F - відома функція. Порядок найвищої похідної, що входить у рівняння (1), називається порядком дифер-го рівняння.

Означення . Розв’язком диференціального рівняння (1) називається n раз диференційована функція y  f(x) , яка при підстановці у рівняння (1) перетворює його в тотожність. Графік розв’язку диференціального рівняння (1) називається інтегральною кривою цього рівняння. Множина усіх розв’язків диференціального рівняння називається його загальним розв’язком. Розв’язати диференціальне рівняння – значить знайти його загальний розв’язок. В ряді випадків його можна подати у вигляді y  f(x, C1,..., Cn) , де C1 , ..., Cn - довільні сталі на деяких проміжках. Частіше загальний розв’язок диференціального рівняння одержують у неявному вигляді f(x, y, C1,..., Cn)  0

Теорема існування і єдності розв’язку. Задача Коші завжди має розв’язок і при тому єдиний. Якщо права частина диф. Рівн. у'=f(x,y) як ф-ія двох змінних визначена і непер в області Д, що містить точку М0(х0,у0) і має неперервні частинні похідні, при чому дf/дy≠0 в точці Мо. 11.Диференціальні рівняння 1 -го порядку з відокремленими змінними.

Диференціального рівняння першого порядку має вигляд F(x, y, y')  0, (2) яке в деяких випадках можна записати у вигляді y'  f(x, y), (3) тобто у вигляді, розв’язаному відносно похідної. Найпростішим прикладом диференціального рівняння (3) є рівняння y'  f(x), (4) де x (a; b) , а функція f(x) - неперервна на інтервалі (a; b).

Означення. Диференціальним рівнянням з відокремлюваними змінними називається рівняння виду y'  f1 (x)  f2 (y), (5) де f1 (x), f2(y) – неперервні функції. Знайдемо розв’язок рівняння (5)

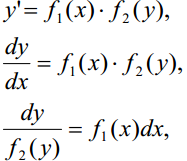тоді