12.Однорідні диференціальні рівняння 1 -го порядку.

Означення. Функція f(x, y) називається однорідною n - го степеня відносно аргументів x і y, якщо для будь-якого числа t  0 має місце тотожність f(tx, ty)  tⁿ f(x, y).

Диференціальне рівняння y'  f(x, y) називається однорідним, якщо його права частина f(x, y) є однорідною функцією нульового степня. Інтегрування однорідного диференціального рівняння за допомогою спеціальної підстановки зводиться до інтегрування рівняння з відокремлюваними змінними. Для цього рівняння спочатку перетворюють до вигляду

Потім використовують підстановку y  ux , тоді y  ux  u, ux  u  (u),

13.Лінійні диференціальні рівняння 1 -го порядку.

Означення. Лінійним диференціальним рівнянням першого порядку називається рівняння виду y' p(x) y  q(x), де функції p(x) і q(x) неперервні на інтервалі (a; b). Будемо шукати розв’язок диференціального рівняння методом Бернуллі у вигляді добутку y  U V двох функцій U(x) і V(x) , тоді: y  UV UV .

Таким чином, U'V UV' p(x) UV  q(x), U'V U(V'V  p(x))  q(x) . Функцію V(x) візьмемо такою, щоб V'V  p(x)  0 , тобто

Тоді для функції U маємо рівняння

Підставимо U і V у рівність y  U V і знайдемо розв’язок рівняння. 14.Диференціальне рівняння Бернуллі.

Диференціальне рівняння вигляду: називаєтьсярівнянням Бернуллі. У цьому рівнянні p(x) і q(x) – деякі неперервні функції, які можуть бути і сталими. Рівняння Бернуллі являє собою нелінійне рівняння оскільки невідома функція y x( ) в праву частину рівняння входить нелінійно. Рівняння Бернуллі можна розв’язати, зведенням його до лінійного, якщо застосувати заміну змінної:

Поділивши обидві частини рівняння на ^yn , одержимо:

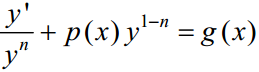
Тепер замість функції y x( ) введемо нову функцію z(x)  y^1n . Для першої похідної цієї функції маємо: Підставимо одержані співвідношення у початкове рівняння і отримаємо лінійне диференціальне рівняння відносно функції z , а саме, , алгоритм розв'язання якого нам вже відомий.15.Диференціальні рівняння 2-го порядку. Інтегрування найпростіших типів y y " " f( f x ( , x y' ); ); рівнянь 2-го порядку, які допускають зниження порядку y" f( y, y' ).

Диференціальне рівняння другого порядку має вигляд Fx, y, y, y  0 , або, якщо воно розв’язане відносно y : y  fx, y, y

1. Рівняння виду y  f(x) , де права частина залежить лише від змінної x Розв’язок такого рівняння знаходиться за допомогою двох послідовних інтегрувань

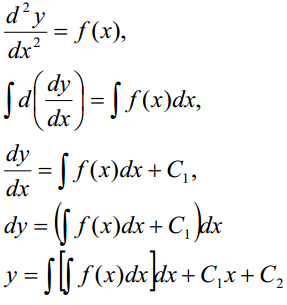
2. Рівняння виду y  f(x; y) (тобто у рівнянні такого типу відсутня шукана функція y ). Рівняння розв’язують за допомогою підстановки y  z(x) , тоді y  z(x)

z’=f(x,y)

z=φ(x,c1)

y’=φ(x,c1)

dy/dx=φ(x,c1) => ʃdy=ʃφ(x,c1)dx

y= ʃφ(x,c1)dx+c2

3. Рівняння виду y  f(y; y) (тобто права частина рівняння не містить аргументу x ). Рівняння розв’язують за допомогою підстановки y’=z(y)

y’’=z’z

z’z=f(y,z)

z=φ(y,c1)

y’= φ(y,c1)

dy/dx= φ(y,c1) => ʃdy/ φ(y,c1)=ʃdx=x+c2 16.Лінійні однорідні диференціальні рівняння 2-го порядку. Означення і загальні властивості.

Означення: д. р. 2-го порядку називається лінійним, якщо містить шукану ф-ію у, у’,y’’ і не містить їх добутку.

Загальний вигляд: y'' py'qy  0 (1)

Властивості:

1) якщо у1(х) і у2(х) – розв’язки рів-ня (1), то

у=с1у1(х) + с2у2(х) – є також розв’язком рів-ня (1) при будь-яких у1,у2

2) два розв’язки у1(х) і у2(х) рів-ня (1) є лінійно незалежними, якщо їх відношення не є сталим;

Якщо у1(х) і у2(х) – лінійно незалежні, то у=с1у1(х)+с2у2(х) – загальний розв’язок рів-ня (1) 17.Лінійні однорідні диференціальні рівняння 2-го порядку зі сталими коефіцієнтами.

Нехай потрібно знайти загальний розв’язок рівняння y'' py'qy  0 (1)

Загальним розв’язком буде ф-ія y  C1 y1 (x)  C2 y2 (x), с1, с2 – const, y1, y2 – частинні розв’язки

Таким чином, щоб знайти загальний розв’язок рівняння необхідно знайти два його лінійно незалежні частинні розв’язки . Будемо шукати розв’язки рівняння у вигляді y  e^kx . Тоді y' ke^kx, y'' k²e^kx і має місце рівність k²e^kx  pke^kx  qe^kx  0, або (k²  pk q)e^kx  0. Оскільки e^kx  0 для будь-якого x R і будь-якого k  R , то ця рівність можлива лише тоді, коли число k є коренем рівняння k²  pk  q  0 . (2) Рівняння (2) називається характеристичним рівнянням рівняння (1). Характеристичне рівняння може мати дійсні або комплексні корені. Можливі три випадки. 1) D  p 2  4ac  0 – корені рівняння дійсні і різні k1  k2 , тоді частинні розв’язки мають вигляд y1  e^k1x , y2  e^k2x . Доведемо, що вони є лінійно незалежними. Складемо лінійну комбінацію: Оскількиk1  k2 , то функція в правій частині є сталою лише за умови, що C2  0 , звідки випливає, що C1  0 , тобто функції y1  e^k1x і y2  e^k2x є лінійно незалежними. Таким чином, загальний розв’язок рівняння (1) має вигляд 2) D  p 2  4ac  0 – корені рівняння дійсні і рівні k1  k2  k , тоді лінійно незалежними будуть частинні розв’язки y1  e^kx і y2  xe^kx , а отже, загальний розв’язок рівняння (1) матиме вигляд

3) D  p 2  4ac  0 – корені рівняння комплексні числа k1    i , k2    i . В цьому випадку загальний розв’язок рівняння (1) має вигляд y  C1e^x cos x  C2e^x sin x 18.Неоднорідні лінійні диференціальні рівняння 2-го порядку. Метод варіації довільних сталих.

Означення. Лінійним неоднорідним диференціальним рівнянням другого порядку із сталими коефіцієнтами є рівняння виду y'' py'qy  f(x), (1) де функція f(x) неперервна на інтервалі (a; b), p, q  R . Рівняння y'' py'qy  0, (2) називається відповідним однорідним для рівняння (1). Має місце наступна теорема про загальний розв’язок неоднорідного лінійного рівняння (1). Теорема. Загальний розв’язок y(x) лінійного неоднорідного рівняння (1) має вигляд y(x)  y(x)  Y, (3) де y(x) - загальний розв’язок відповідного однорідного лінійного рівняння (2). Y - частинний розв’язок лінійного неоднорідного рівняння (1), Лагранж запропонував шукати розв’язок Y(x) рівняння (1) у вигляді Y(x)  C1 (x) y1 (x)  C2 (x)y2 (x), (4) де C1(x) і C2(x) - невідомі функції. Тоді Y'(x)  C1 ' y1  C1 y1 'C2' y2  C2 y2 ' . Накладемо на функції C1(x) і C2(x) умову

, (5) тоді Y'(x)  C1 y1 'C2 y2' , звідки Y''(x) C1' y1'C1 y1 ''C2' y2'C2 y2'' . Підставляючи Y,Y',Y у рівняння (1), будемо мати: C1' y1'C1 y1''C2' y2'C2y2''p(C1 y1'C2y2')  q(C1 y1  C2y2)  f(x), C1' y1'C2' y2'C1(y1'' py1'qy1)  C2(y2'' py2'qy2)  f(x), звідки C1' y1'C2' y2'  f(x)(6)

Оскільки y1 і y2 є розв’язки відповідного однорідного рівняння (2), то

Рівняння (5) і (6) утворюють систему

(7)

яку повинні задовольняти функції C1(x) і C2(x) . Визначник системи (7)

(8)

оскільки відношення функцій y1/y2 або y2/y1 не є сталим. Дійсно, похідні

звідки   0 . Тому система (8) має єдиний розв’язок C1' і C2' . Інтегруючи функції C1' і C2' , знайдемо C1(x) і C2(x) , а, отже, і функцію Y(x)  C1 (x) y1 (x)  C2 (x) y2 (x) . 19.Метод невизначених коефіцієнтів для знаходження частинного розв’язку лінійного неоднорідного диференціального рівняння зі сталими коефіцієнтами і правою частиною виду: f(x) Pn (x)eax а) ; f( x) eax (Pn ( x) cos bx Qm ( x) sin bx). б)

Другий метод знаходження розв’язку Y(x) має назву методу невизначених коефіцієнтів. Він придатний для рівнянь із сталими коефіцієнтами і спеціальною правою частиною. Нехай f(x)  Pm (x)e^x , де Pm(x) - многочлен степеня m  0 . Можливі випадки 1) число  не є коренем характеристичного рівняння, тоді частинний розв’язок неоднорідного рівняння шукають у вигляді Y(x)  e^xQ_m (x), де Qm (x) - многочлен степеня m з невизначеними коефіцієнтами: Q_m(x)  q0  q1x ...  q_mx_m. 2) число  збігається з коренем характеристичного рівняння, тоді Y(x)  xe^xQ_m(x) де Qm (x) - многочлен степеня m з невизначеними коефіцієнтами: Q_m(x)  q0  q1x ...  q_mx_m. 3) число  збігається з обома коренями характеристичного рівняння, тоді Y(x)  x²e^xQ_m (x), де Qm (x) - многочлен степеня m з невизначеними коефіцієнтами: Q_m(x)  q0  q1x ...  q_mx_m. Для того, щоб знайти коефіцієнти q0, q1 ,...qm необхідно частинний розв’язок 1), 2) або 3) підставити у рівняння y'' py'qy  f(x) . Прирівнюючи коефіцієнти при однакових степенях x в обох частинах рівняння, дістанемо систему, з якої знайдемо невідомі коефіцієнти q0, q1 ,...qm . Нехай f(x)  P_m(x)e^xcosxR_s(x)e^xsinx, де Pm(x) і Rs(x) - многочлени степенів m і s відповідно. Можливі випадки 1) число   i не є коренем характеристичного рівняння, тоді частинний розв’язок неоднорідного рівняння шукають у вигляді Y(x)  Q_k (x)e^x cos  x  T_k (x)e^x sin  x, де Qk (x),Tk (x) - многочлени степеня k з невизначеними коефіцієнтами: k  max(m, s) 2) число   i збігається з коренем характеристичного рівняння, тоді Y(x)  xQ_k (x)e^x cos  x  T_k (x)e^x sin  x, де Qk(x),Tk (x) - многочлени степеня k з невизначеними коефіцієнтами: k  max(m, s) Нехай f(x)  M cos x  Nsin x, де M, N – деякі числа. Можливі випадки 1) число i не є коренем характеристичного рівняння, тоді частинний розв’язок неоднорідного рівняння шукають у вигляді Y(x)  Acos  x  Bsin  x, де A, B - невідомі сталі 2) число i збігається з коренем характеристичного рівняння, тоді Y(x)  xA cos  x  Bsin  x 20.Числові ряди. Сума ряду. Збіжні і розбіжні ряди. Властивості збіжних рядів.

Означ. Нехай задана нескінченна послідовність a1, a2 , …, a_n , …. Тоді вираз 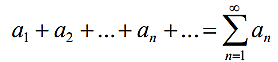(1) називається числовим рядом. Числаa1, a2 , …, a_n , … називаються членами ряду, a_n – загальний член ряду. Розглянемо часткові суми ряду Означ. Сума n –перших членів ряду називається частковою сумою. Зокрема,

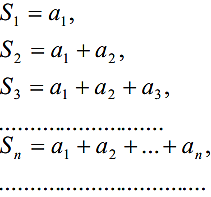
Послідовність часткових сум ряду (1) може бути збіжною або розбіжною. Означ. Ряд називається збіжним, якщо послідовність (Sn ) його часткових сум збіжна, а границю S послідовності (Sn ) називають сумою ряду і пишуть . Якщо послідовність (Sn ) часткових сум ряду (1) розбіжна, то ряд (1) називається розбіжним і ніякої суми йому не приписують.

Якщо в ряді (1) відкинути перші n членів, то отримаємо ряд (2) який називаєтьсязалишком ряду (1).

Властивості збіжних рядів 1. Ряд і довільний його залишок одночасно збіжні або розбіжні. 2. Якщо рядзбігається і має суму, то збігається і ряд, який одержано із даного добутком кожного члена даного ряду на стале числоλ, та сума цього ряду дорівнює 3. Якщо ряди із загальними членамиa_n та b_n збігаються та відомі суми для кожного ряду: та, тоді для будь-яких чиселα та β ряд із загальним членом: є збіжним, а його сума дорівнює: .Твердження доводяться на основі властивостей границь. 21.Необхідна ознака збіжності ряду. Гармонічний ряд.

Теорема ( необхідна ознака збіжності ряду). Якщо ряд збіжний, тоді (3) Доведення. Нехай ряд збіжний. ТодіАле. Отже,Наслідок. Якщо загальний член ряду (1) не прямує до нуля при n →∞ , то ряд (1) розбіжний.

Означення. Гармонічним називається ряд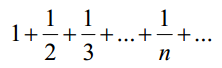Можна показати, щогармонічний ряд – розбіжний 22.Ознаки порівняння рядів. Приклади.

Перша ознака порівняння. Якщо для рядів з додатними членами

u1 + u2 + ... + un + ... , (1)

v1 + v2 + ... + vn + ... (2)

виконується умова u_n≤v_n , тоді:

а) якщо ряд (2) збігається, то збігається і ряд (1);

б) якщо ряд (1) розбігається, то розбігається і ряд (2)

Приклад. Дослідимо на збіжність ряд Порівняємо його з рядомЦей ряд збігається, оскільки послідовність його членів являє собою нескінченно спадаючу геометричну прогресію із знаменником q = 1 / 2, сума якої дорівнює 1/2. При будь-якому, тому за теоремою ряд збігається.

Друга ознака порівняння. Якщо для рядів (1) і (2) виконується умова

то ряди (1) і (2) збігаються і розбігаються одночасно

Приклад. Дослідимо ряд

Загальний член ряду можна подати у вигляді (поділивши чисельник та знаменник на n). Тепер очевидно, що

Оскільки ряд збігається (р = 2 >1), то за теоремою збігається і даний ряд. 23.Ознака Даламбера збіжності ряду.

Якщо для ряду , існує границя: , то при l < 1 ряд збігається, а при l > 1 розбігається 24.Радикальна ознака Коші збіжності ряду.

Якщо для ряду , існує границя, то при l < 1 ряд, збігається, а при l > 1 розбігається 25.Інтегральна ознака Коші збіжності ряду.

Нехай функція f(x) - невід’ємна, неперервна і незростаюча на проміжку [1;  ) . Тоді ряд і невласний інтеграл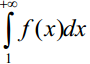одночасно збіжні або розбіжні. 26.Знакопочережні ряди. Теорема Лейбніца.

Для числових рядів, сусідні члени яких мають різні знаки і називаються знакопочережними, розрізняються два види збіжності. Ряд називається абсолютно збіжним, якщо збігається ряд модулів його членів, тобто ряд.

Теорема. Якщо ряд збігається абсолютно, то він збігається і в звичайному сенсі, тобто існує скінченна границя його часткових сум.

Зауваження. Оскільки ряд знакододатний, то для дослідження знакопочережного ряду на абсолютну збіжність ми можемо використати всі ознаки збіжності знакододатних рядів.

Якщо знакопочережний ряд не збігається абсолютно, то необхідно відповісти на питання, чи буде він збігатися хоча б умовно. Відповідь на це питання можна знайти, застосувавши ознаку Лейбніца.

Теорема. Якщо члени знакопочережного ряду u₁ – u₂ + u₃ – u₄ +…, де u_i > 0 задовольняють умови: 1) u₁ > u₂ > u₃ >… > u_n > u_n+1 >… (наступний член ряду за модулем менше попереднього); 2) то ряд збігається (хоча б умовно), його сума 27.Знакозмінні ряди. Достатня ознака збіжності знакозмінного ряду.

Означення. Знакозмінним рядом називається ряд, який містить як додатні, так і від’ємні члени.

Теорема (достатня ознака збіжності) . Нехай задано знакозмінний ряд Тоді, якщо рядє збіжним, то і ряд також є збіжним. 28.Знакозмінні ряди. Абсолютна і умовна збіжність.

Означення. Знакозмінним рядом називається ряд, який містить як додатні, так і від’ємні члени.

Означення. Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд

Означення. Знакозмінний ряд називається умовно збіжним, якщо ряд є розбіжним. 29.Степеневі ряди. Інтервал збіжності.

Якщо членами ряду є функції 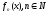, визначені в спільній області існування D, то маємо функціональний ряд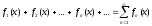(1)

При фіксованому 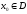ряд (1) стає числовим, який буде збіжним або розбіжним

Якщо в точці 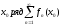збіжний, то число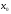називають точкою збіжності ряду (1), а множину всіх точок збіжності називають областю збіжності ряду.

Означення. Степеневим рядом називається ряд виду

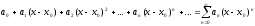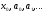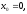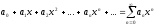, (2) де - дійсні або комплексні числа. Особливо простим ряд (2) стає притобто(3)

Теорема Абеля.

1. Якщо степеневий ряд збігається при x=x₀ , то він буде абсолютно збіжним при всіх

значеннях x , що задовольняють умову .

2. Якщо степеневий ряд розбігається при x=x₁ , то він буде розбіжним при всіх

значеннях x , що задовольняють умову .

Таким чином, із теореми Абеля випливає, що існує таке число R≥0 , що при |x|< R ряд є збіжним, а при |x|>R – розбіжним.

Число R називається радіусом збіжності степеневого ряду.

На кінцях інтервалу, тобто при x=-R , x=R ряд може буди як збіжним, так і розбіжним.

Використовуючи ознаку Даламбера можна отримати формулу для знаходження радіуса збіжності

степеневого ряду:

Формула Коші-Адамара 30.Ряди Тейлора і Маклорена.

Розглянемо степеневий ряд (1)

Якщо степеневий ряд збіжний на інтервалі (-r; r) , то його сумою є деяка функція f(x) , визначена

на інтервалі (-r; r) , тобто

(2)

У цьому випадку кажуть, що функція розвинута у степеневий ряд на інтервалі його збіжності.

Оскільки , деS_n(x) - частинні суми степеневого ряду (1), то для достатньо

великих n маємо наближену рівність , яка дуже важлива для практики. Справа в тому, що частинні суми степеневого ряду є многочленами, які обчислюються дуже просто. Функція жf(x) може бути або взагалі невідомою, або її обчислення громіздке. Тоді використовують наближену рівність .

Диференціюючи почленно рівність (2), в інтервалі (-r; r) отримаємо:

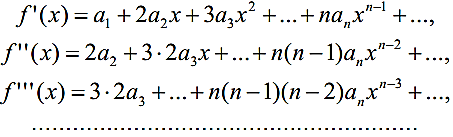
Якщо x=0 , тоді маємо

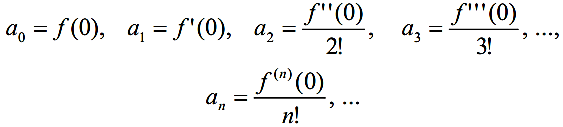(3)

Таким чином, коефіцієнти a_n (n=0,1,...) степеневого ряду (1) визначаються через функцію f(x) і

її похідні за формулами (3) і ряд (1) можна записати у вигляді

(4)

Ряд (4) називається рядом Маклорена функції f(x) .

Якщо аналогічно обчислити коефіцієнти степеневого ряду , то отримаємо

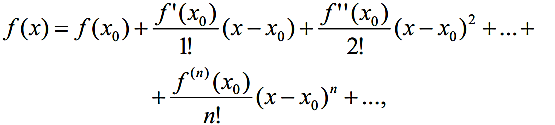
Степеневий ряд (5) називається рядом Тейлора функції f(x).

Теорема 1. Якщо функція f(x) в інтервалі (x₀- r; x₀+r) розвивається у степеневий ряд (5), то це

розвинення єдине і є рядом Тейлора функції f(x) .

Ряд Тейлора формально можна записати для кожної нескінченно диференційовної в інтервалі

(x₀- r; x₀+r) функції f(x) . Але рівність (5) має місце не для кожної такої функції. Для виконання

рівності (5) функція f(x) повинна задовольняти додаткові умови. Вони розглядаються в наступній

теоремі.

Теорема 2. Для рівності (5) необхідно й достатньо виконання умови (6)

для будь-якого - частинні суми ряду Тейлора.

Умову (6) задовольняють функції f(x) , що мають в інтервалі (x₀- r; x₀+r) обмежені

похідні всіх порядків .

За формулою Тейлора для таких функцій f(x) має місце рівність

де точка C лежить між точками x₀ і x. Зокрема, умову (6) задовольняють функції sin x, cos x, e^x .

Розвинення у степеневий ряд деяких елементарних функцій

Наведемо розклади в ряд Маклорена деяких елементарних функцій:

,,