29. Степеневі ряди. Інтервал збіжності.

Ряд виду а₀+а₁х+а₂х²+.... називається степеневим рядом, а числа а₀,а₁,а₂,....- коефіцієнтами степеневого ряду.

Теорема Абеля:1)якщо степеневий ряд збігається при значенні х=х₀≠0, то він збігається і , причому абсолютно, при всіх значеннях х таких, що |x|<|x₀|.2)Якщо степеневий ряд розбігається при х=х₁, то він розбігається при всіх значеннях х таких, що |x|>|x₁|.

Доведення

1)За умовою степеневий ряд збігається при х=х₀≠0, значить виконується необхідна умова збіжності

lim u_n=lim a_nx₀ⁿ=0

n∞ n∞

Звідси випливає, що послідовність |a_nx₀ⁿ| обмежена, т.е. існує таке число М>0, що для всіх n виконується нерівність

|a_nx₀ⁿ|<M.(1)

Розглянемо ряд, складений із абсолютних величин членів ряду. ∑(от n=1 до ∞ )|a_nx₀ⁿ|, який представимо у вигляді |a₀|+|a₀x₀||x/x₀|+….+|a_nx₀ⁿ||x/x₀|ⁿ+….

Члени цього ряду згідно нерівності (1) менші відповідних членів ряду М+М|x/x₀|+....+М|x/x₀|ⁿ +..., який являє собою геометричний ряд, який збігається, коли його знаменник q=|x/x₀|<1, тобто |x|<|x₀|, значить на основі умови порівняння ряд а₀+а₁х+а₂х²+.... збігається.

2)За умовою ряд а₀+а₁х+а₂х²+.... розбігається при х=х₁. Покажемо, що він розбігається для усіх х, задовольняючих умові |x|>|x₁|. Припустимо зворотне, тобто при |x|>|x₁| ряд збігається. Тоді за доведеним вище він повинен збігатися і в точці х₁(бо |x|<|x₀|), щ оне задовольняє умові. Таким чином, для всіх х таких, що |x|>|x₁|, ряд а₀+а₁х+а₂х²+.... розбігається.

20.Ряд Тейлора і Маклорена.

Якщо ф-ція y= f(x) неперервна в деякому інтервалі, що містить точку х = а і в цьому інтервалі має неперервні похідні від 1-го до n-го порядку включно, то вона може бути представлена у вигляді многочленна n-го порядку і залишкового члена R_n(x) по формулі Тейлора Припустимо, що ф-ціяf(x) має похідні до (n+1)-го порядку включно в околі точки х=а, тоді залишковий член R_n(x) можна записати у Формі Лагранжа а<с<х (х<с<а)

Якщо в формулі Тейлора покласти а=0, то одержимо формулу Маклорена:

Якщо ф-ція f(x) має в деякому інтервалі, що містить точку х=а похідні любого порядку і якщо залишковий член R_n(x) в формулі Тейлора прямує до 0 при необмеженему зростанні n, то одержимо ряд Тейлора Зокрема, якщо а=0 одержимо ряд Маклорена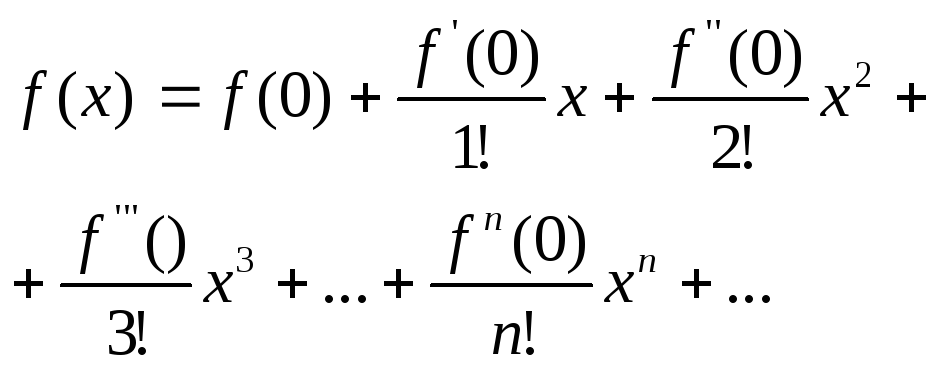(1) Ф-ціяf(x) може бути розвинена в ряд Маклорена, якщо вона має похідні любого порядку, тобто нескінченно диференційована в точці х=а. Для розвинення в ряд Маклорена необхідно і досить, щоб залишковий член ряду R_n(x)→0, тобто (2) Якщо умова 6 не виконується, то степеневий ряд в правій частині формули 1 не є ф-цієюf(x). Якщо умова 6 виконується на деякому проміжку, то на цьому ж проміжку складений ряд Маклорена збігається до ф-ції f(x). Умову 6 записати у вигляді Так як є заг. член ряду, який збіг-я при любому знач. Х. А отже за необх умовою збіж ряду , а значить умова 6 буде вик-ся на любому проміжку, на якому величина f⁽ⁿ⁺¹⁾(c) 0<c<x є обмеженою.

Роскладання функції в степеневий ряд

Найближче обчислення інтегралів за допомогою рядів

Можливість розвинення функції у степеневий ряд дозволяє спростити багато математичних операцій: обчислення наближених значень даної функції, диференціювання, інтегрування, оскільки степеневий ряд можна замінити многочленом ( з урахуванням того, що оцінка залишку ряду не перевищує заданого значення похибки). Зокрема, можна наближено обчислювати інтеграли, що не «беруться», знаходити наближені рішення диференціальних рівнянь.