13.Лінійні однорідні диф. Р-ня 2-го пор. Зі сталими коефіцієнтами

(1), p,q-const,-- однорідне лінійне р-ня з сталими коефіцієнтами.

Заг. розв’язком р-ня буде ф-я (2), де у₁ і у₂ – два лінійно незалежні частинні розвязки цього р-ня. Для знаходження частинних розв’язків у₁ і у₂ припустимо, що ф-я, де к-стале число, є розв’язком р-ня (1). Знайдемо у^, і у^,,. ,. Підставимо у^, і у^,, в р-ня (1). ,; так як, то(3). Р-ня (3) наз. характеристичним р-ням для р-ня(1).

При рішенні характеристичного квадратного р-ня можливі наступні випадки:

1. Корні характеристичного р-ня дійсні і різні , тоді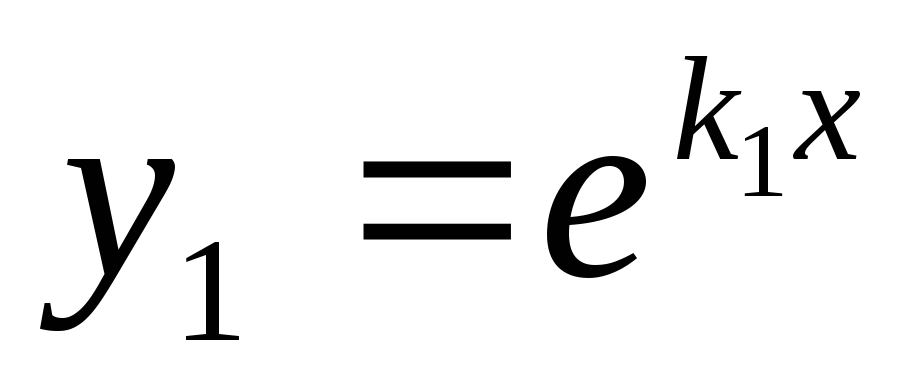,- лінійно незалежні розвязки цього рівняння. Так як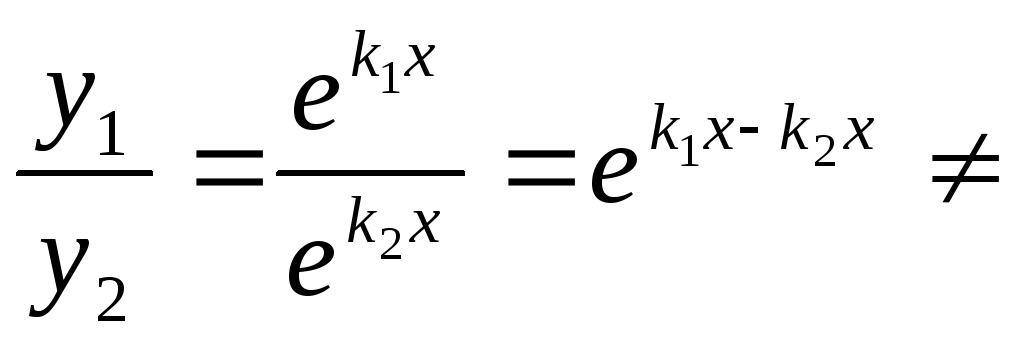const, тоді загальний розвязок р-ня (1) має вигляд, де С₁ і С₂ –const.

2. Корені хар. р-ня дійсні і рівні між собою , тоді заг. розвязок р-ня (1) -, де С₁ і С₂ –const.

3. Корені хар. р-ня комплексні , тоді заг. розвязок р-ня (1) -, де С₁ і С₂ –const.

18.Неоднорідні лінійні диференціальні рівняння 2-го порядку. Метод варіації довільних сталих.

Методом невизначених коефіцієнтів можна скористуватися тільки в тих випадках, коли права частина диференціальної рівняння є функція виду : многочлен, показникова ф-ці я sin x, cos x. В тих випадках коли права частина див. рівняння відмінна від вище названих ф-ці застосовують метод варіаційних сталих(метод Лагранжа).Нехай задано неодорідне диню р-ня: y’’+ p(x)y’ +g(x)y=f(x) [1] Рівняння [1]має розв’язок Y=y¹+y² ,де y² це загальний розв’язок однорідного рівняння, а y² частинний розв. неоднорідного рів.

Нехай (3)загальний розв’язок однорідного рів.(2) де y₁ I y₂ два лінійно незалежні частинні розв’язки з-ня (2). Частинний розв’язок (1) будемо шукати формі [3] ,припустивши , що С₁ і С₂ деякі ф-ці від х. с₁=с₁(х), с₂=с₂(х). Продифкренціюємо рівність (3) одержимо

. Підберемо с₁ і с₂ так що с₁’y₁+c₂’y₂ = 0,тоді y’=c₁y₁’+c₂y₂’. Продифкренціюємо цей вираз і знайдемо у^,,

. Значення y y’ y’’ підставимо у рівняння (1).

Одержимо С₁’y₁’+С₂’y₂’+С₁y₁’’+С₂y₂’’+p(x)(С₁y₁’+С₂y₂’) +g(x)

(С₁y₁+С₂y₂)=f(x) ; С₂(y₂’’+p(x)y₂’+g(x)y₂ )+С₁(y₁’’+p(x)y₁’+g(x)y₁ )+С₁’y₁’+С₂’y₂’=f(х) Оскільки y₁ I y₂ частинні розв’язки р(2) , то

y₂’’+p(x)y₂’+g(x)y₂=0 , y₁’’+p(x)y₁’+g(x)y₁=0, тоді С₁’y₁’+С₂’y₂’=f(x). Таким чином ф-я y=С₁(x)y₁+С₂(x)y₂ буде рішенням р.(1), якщо ф-ї С₁ і С₂ будуть задовольняти систему Розв’язавши цю систему знайдемо С₁ і С₂ Одержимо,, звідси-const;-const. Загальний розвязок:

Метод невизначених коефіцієнтів для знаходження частинного розв’язку

лінійного неоднорідного диференціального рівняння зі сталими

коефіцієнтами і правою частиною виду:

а) ax f (x) Pn(x)e ;

б) f (x) e (Pn(x) cosbx Qm(x)sinbx).

15. Системи диференціальних рівнянь 1-го порядку. Метод виключення змінних.

16.Числові ряди. Сума ряду. Збіжні і розбіжні ряди. Властивості збіжних рядів. Числовим рядом називають вираз виду а₁+а₂+а₃+….+а_п+..=(1), де а_п – числа, що належать певній системі. Для скороченого позначення рядів використовують знак суми .

Числа а_1, а₂, а₃,…,а_п,.. називаються членами ряду, а_п – загальний член ряду.

Приклади числових рядів:

а). із членів нескінченної геометричної прогресії можна скласти ряд

а₁+а₁q+а₁q²+a₁q³+….+a₁q^n-1+…=

б). ряд складається із чисел обернених натуральним числам

1+1/2+1/3+1/4+…+1/п+…=- гармонічний ряд.

Сума перших п-членів ряду назив. частинною сумою ряду і позначається.

Таким чином з рядом (1) пов’язана послідовність його частинних сум S₁, S₂, S_3,…., S_n де S₁=a_1, S₂= a₁+a₂, S₃= a₁+a₂+a₃, S_n= a₁+a₂+a₃+…+a_n.

Ряд називається збіжним , якщо послідовність його частинних сум збігається, тобто існує скінченна границя . Число S називається сумою ряду. Якщоне існує або дорівнює, то ряд розбігається, розбіжний.

Приклад: дослідити на збіжність ряд ln2+ln3/2+ln4/3+ln5/4+…+ln(n+1/n)+…

S_n=ln2+ln3/2+ln4/3+ln5/4+…+ln(n+1/n)=ln(n+1).

- ряд розбіжний.

Розглянемо ряд нескінченної геометричної прогресії а₁+а₁q+а₁q²+a₁q³+….+a₁q^n-1+…

Сума перших п- членівабо. Дослідимо ряд на збіжність в залежності від значенняq:

lim S_n-не існує. Таким чином рядпри-збіжний, а при-розбіжний.

Властивості збіжних рядів.

Теорема 1: Якщо ряд збігається, який одержано із даного ряду відкиданням декількох його членів, то і збіжним є і сам ряд. І навпаки: якщо збігається даний ряд, то збігається і ряд, який одержано із даного відкиданням декількох членів. Іншими словами, на збіжність ряду не впливає відкидання скінченого числа членів.

Теорема 2 : Якщо ряд а₁+а₂+а₃+а_n+… збігається і його сума = S_n, то ряд са₁+са₂+са₃+са_n+… збігається і його сума = с S_n.

Теорема 3: Якщо ряди а₁+а₂+а₃+а_n+… і b₁+b₂+b₃+b_n+… -збігаються і їх суми S₁ і S₂ – відповідно, то ряди (а₁₊ b₁)+ (а₂₊ b₂)+…+( а_n+ b_n)+… і (а₁- b₁)+ (а₂- b₂)+…+( а_n- b_n)+… збігаються і їх суми = S₁+S₂ і S₁-S_2.

Необхідна ознака збіжності ряду. Гармонічний ряд.

В математиці, гармонічним рядом називається нескінченний розбіжний ряд: